논문 제목 : Learning Latent Dynamics for Planning from Pixels

Danijar Hafner, Timothy Lillicrap, Ian Fischer, Ruben Villegas, David Ha, Honglak Lee, James Davidson
2018
논문 링크

Summary

PlaNet은 Latent State 만으로 Planning을 진행하고, 별도의 Policy Network 없이 Planning의 결과만을 바탕으로 Action을 결정하는 Model-Based Algorithm이다.
Observation(Image Input)을 처리하는 데에 소요되는 자원을 줄이기 위해 Latent Space 상에서 Prediction과 Loss 계산을 수행한다.
Recurrent State Space Model을 적용하여 robust하면서도 학습이 잘 되는 Prediction이 가능하도록 하고 있고, Latent OverShooting으로 Latent State 상에서 Multi-Step Prediction을 적은 비용으로 수행할 수 있도록 한다.

Model-Based Reinforcement Learning

**Model-Based Reinforcement Learning(Model-Based RL)**이란 Agent가 Environment의 Dynamics를 학습하고 이를 통해 미래의 State, Action Sequence를 예측하여 현재 시점에서 최적의 Action을 결정하도록 하는 강화학습 방법론이다. Model-Based RL은 Agent가 경험하여 정확도가 높은 Model을 이미 가지고 있는 Enviroment에 대해서는 매우 효과적이다. 하지만 어떤 Enviroment에 대해 그것이 가지고 있는 Dynamics를 이해하여 어떤 Action에 의한 Next State를 정확하게 계산해내는 Model을 만드는 것은 결코 쉽지 않다. DQN, DDPG와 같은 Model-Free 방법론이 강화학습 분야에서 핵심 알고리즘으로 기능했던 이유 또한 여기에 있다.

이와 관련하여 논문에서는 Model-Based RL이 가지는 일반적인 어려움들을 다음 네 가지로 정리하고 있다.

Model의 부정확성
Multi-Step 예측에 있어 누적되는 오차
동일한 상황에서 다양한 가능성의 존재
학습 환경과의 차이로 인한 예측 실패

반면 높은 성능의 Model을 활용한 Planning으로 강화학습의 문제를 해결하는 것의 장점도 기술하고 있다.

데이터 효율적이다.
더 많은 Action에 대해 탐색하는 것으로 성능을 높일 수 있다.
Task간 Transfer learning이 가능할 수 있다.

Planning with Image

이와 같은 원론적인 문제와 함께 이미지 등 높은 차원의 State를 가지는 경우에는 Planning에 많은 비용이 들어가고, 정확도 또한 좋지 못한 문제가 추가적으로 발생한다. 이러한 문제를 해결하기 위해 많은 방법론들이 Enviroment에서 받는 State의 Dynamics를 그대로 학습하는 것이 아니라, State를 인코딩하여 Latent Space 상에서의 Dynamics를 이해하는 방법을 시도해왔다. PlaNet 또한 Latent Dynamics를 학습하여 Planning을 시도한다.

Problem Steup

PlaNet은 하나의 이미지 Observation을 현재 Enviroment의 State로 보는데, 이를 전체 Environment의 State라 하기에는 매우 부족하다. 이러한 점에서 POMDP(Partially Observable MDP)로 가정한다.

|:---:|:---:| | $s_t \backsim p(s_t \lvert s_{t-1}, a_{t-1})$ | Transition Model(Gaussian) | | $o_t \backsim p(o_t \lvert s_t)$ | Observation Model(Gaussian) | | $r_t \backsim p(r_t \lvert s_t)$ | Reward Model(Gaussian) | | $s_t \backsim q(s_t \lvert o_{\leq t}, a_{<t})$ | Encoder | | $a_t \backsim p(a_t \lvert o_{\leq t}, a_{<t})$ | Policy |

여기서 $o_t$ 는 Environment로부터 전달받은 이미지를, $s_t$ 는 $o_t$ 를 인코딩하여 얻은 Latent State를 의미한다. PlaNet의 목표는 위의 세 가지 Model과 Encoder를 Experience를 통해 학습하여 $E_p[\Sigma_{t=1}^T r_t]$ 를 극대화하는 Policy를 찾는 것이다.

참고로 논문에서 Current State Belief 라는 표현이 자주 등장하는데 이는 Observation을 인코딩하여 얻은 Latent State $s_t \backsim q(s_t \lvert o_{\leq t}, a_{<t})$ 를 지칭한다. 즉, 엄밀히 말해 $s_t$ 는 Environment가 제공하는 State와는 다른 것이기 때문에 Belief라는 표현을 쓰는 것 같다.

Take Action with Planning Algorithm

현재 시점 $t$ 에서 Planning을 통해 Action $a_t$ 를 결정하겠다는 것은 Latent State $s_t$ 에서 시작하여 만들어질 수 있는 무한한 State-Action Sequence 중에서 기대 누적 Reward가 가장 큰 경우에 따르겠다는 것을 뜻한다. 여기서도 최적의 State-Action Sequence를 찾기 위해서는 다양하게 경험해보고 이들 간의 기대 누적 Reward를 비교해보는 것이 중요하다고 할 수 있다.

이를 위해 PlaNet은 매 Optimization Iteration마다 $J$ 개의 Action Sequence를 Action Sampling Distribution $q(a_{t:t+H})$ 에서 Sampling하며(line 3~6), 이 중 Sequence의 기대 누적 Reward $R^{(j)}$ 가 큰 순서대로 $K$ 개를 뽑아(line 7) 이들의 분포로 Action Sampling Distribution을 업데이트하도록 하고 있다(line 9). 초기의 Action Sampling Distribution은 알고리즘에 나와 있듯(line 1) Normal Distribution으로 한다. 결과적으로 $s_t$ 에서의 Action은 $\mu$ 로 결정된다.

참고로 논문의 실험에 사용된 Planning Hyperparameter는 다음과 같다.

Horizon Length $H = 12$
Optimization Iteration $I = 10$
Number of Samples $J = 1000$
Number of Bset Samples $K = 100$

Recurrent State Space Model

이러한 Planning 기반 알고리즘의 문제 중 하나는 매 Step마다 수천 개의 Action Sequence를 평가해야 한다는 것으로, 시간과 비용이 많이 소요된다는 점이다. PlaNet에서는 이를 빠르게 해결하기 위해 Latent Space 상에서 다음 Latent State를 예측하여 빠르게 Planning을 수행하는 모델, **Recurrent State Space Model(RSSM)**을 제안한다.

Apply Variational AutoEncoder

Environment로 부터 얻은 Observation Sequence를 Latent Space로 이동시키기 위해 VAE를 사용하며, 이때 과거의 Observation과 Action으로부터 State Posterior를 추정하는 Encoder는 다음과 같이 나타낼 수 있다.

q(s_{1:T} \lvert o_{1:T}, a_{1:T}) = \Pi_{t=1}^T q(s_t \lvert s_{t-1}, a_{t-1}, o_t)

One-Step Predictive Distribution

VAE의 Lower Bound 식을 먼저 확인해보면 다음과 같다.

\eqalign{ \log p_\theta(x) &\geq \text{lower bound} \ L(\theta, \phi ; x) \\ &= - D_{KL}(q_{\phi}(z \lvert x) \| p_\theta(x)) + E_{z \backsim q_{\phi}(z \lvert x)} [log p_\theta(x \lvert z)] }

여기서 우변의 첫 번째 KLD Term을 Prior $p_\theta(x)$ 와 Posterior $q_{\phi}(z \lvert x)$ 간의 거리를 줄이는 Regularizer, 즉 Encoder 부분이고, 두 번째 Expectation Term이 Reconstruction Error로 Decoder 부분이 된다. PlaNet에서는 Prior가 Action Sequence가 주어져 있을 때 그에 맞는 Observation Sequence를 구하는 것이므로 $p(o_{1:T} \lvert a_{1:T})$ 이 되며, 이를 Encoder 식과 함께 위 식에 적용하면 다음과 같다.

\eqalign{ &1. \text{Prior: } p_\theta (x) \rightarrow p(o_{1:T} \lvert a_{1:T}) = \Pi_t p(s_t \lvert s_{t-1}, a_{t-1}) p(p_t \lvert s_t) \\ &2. \text{Posterior: } q_\theta(x \lvert x) \rightarrow q(s_{1:T} \lvert o_{1:T}, a_{1:T}) = \Pi_t q(s_t \lvert o_{\leq t}, a_{< t})\\ \\ &\eqalign{ \Rightarrow \log p(o_{1:T} \lvert a_{1:T}) \geq & - E_{q(s_{t-1} \lvert o_{\leq t-1}, a_{< t-1})} [\text{D}_{\text{KL}} [q(s_t \lvert o_{\leq t}, a_{< t}) \lvert \rvert p(s_t \lvert s_{t-1}, a_{t-1}) ]] \\ & + \Sigma_{t=1}^T (E_{q(s_t \lvert o_{\leq t}, a_{< t})} [\log p(o_t \lvert s_t)])\\ } }

식을 풀이해보면 Regularizer Term은 인코딩을 통해 얻은 $s_t$ 의 분포 $q(s_t \lvert o_{\leq t}, a_{< t})$ 와 이전 State와 Action을 통해 얻은 $s_t$ 의 분포 $p(s_t \lvert s_{t-1}, a_{t-1})$ 가 최대한 유사해지도록 업데이트 된다는 것을 알 수 있다. 그리고 Reconstruction Error Term에서는 당연히 주어진 $s_t$ 로 그때의 Observation $o_t$ 를 잘 추정할 수 있는 방향으로 업데이트 된다. 위 식과 관련해 자세한 전개식은 논문의 Appendix에 나와있다.

Deterministic and Shocastic Path

이와 관련하여 Transition Model $s_t \backsim p(s_t \lvert s_{t-1}, a_{t-1})$ 과 관련해 이를 Stochastic Model로 할 것인지, Deterministic Model(variance=0)로 할 것인지 또한 중요한 문제가 된다. 왜냐하면 Stochstic하다고 가정하는 경우 Transition Model이 Multiple Step을 예측하는 것을 어렵게 한다는 단점을 가지고, Deterministic하다고 가정하는 경우에는 Optimization 과정에서 Solution을 찾는 것이 너무 어려워 학습이 어려워진다는 단점을 각각 가지기 때문이다.

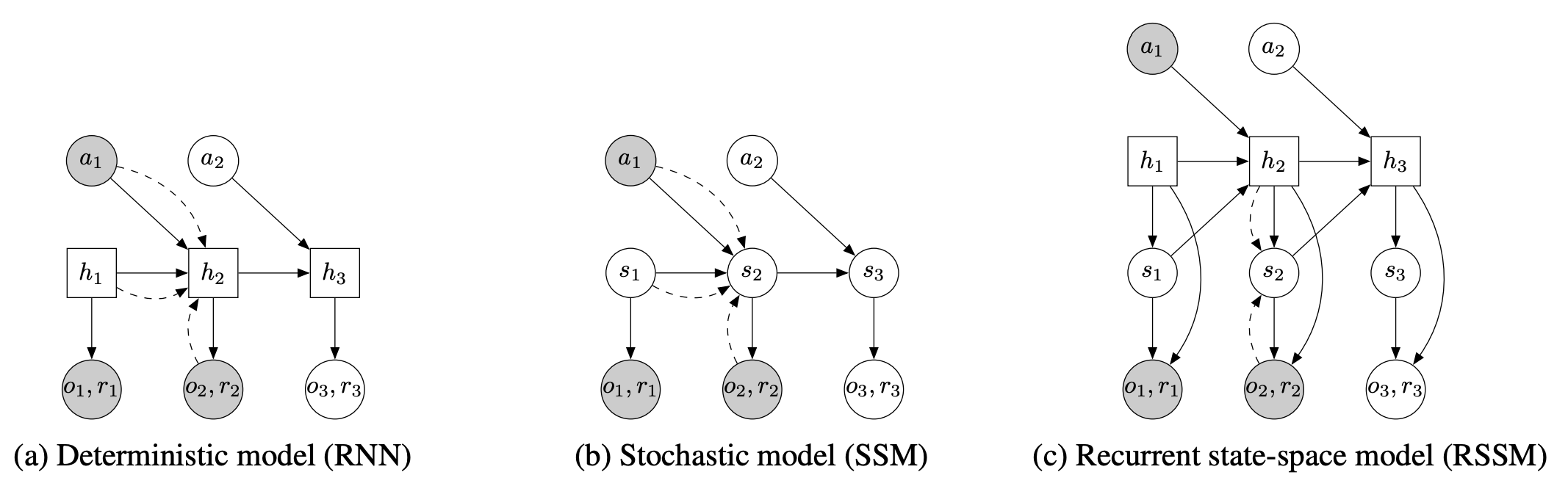
위의 그림에서 원 속의 $s_t$ 는 Stochastic Variable이고 네모 박스의 $h_t$ 는 Deterministic Variable이다. 첫 번째와 두 번째 그림에 나와있는 Deterministic Model은 $h_t$ 만을, Stochastic Model은 $s_t$ 만을 사용하는데 이 경우 위에서 언급한 문제들이 발생한다. 이러한 문제를 피하기 위해 논문에서 제시하는 방법 RSSM은 $h_t$ 와 $s_t$ 를 함께 사용하여 보다 Robust하면서도 Multiple Step 예측에도 효과적인 모델이 될 수 있다고 언급한다.

|---|---| | $h_t = f(h_{t-1}, s_{t-1},a_{t-1})$ | Deterministic State Model | | $s_t \backsim p(s_t \lvert h_t)$ | Stochastic State Model | | $o_t \backsim p(o_t \lvert h_t, s_t)$ | Observation Model | | $r_t \backsim p(r_t \lvert h_t, s_t)$ | Reward Model |

Latent OverShooting

위의 방법에 따라 학습하게 되면 매 시점에서 한 time-step 이후의 State에 대해서만 예측이 이뤄지게 되고, 그것에 대해서만 정확히 예측하도록 학습이 이뤄진다. 사실 매 시점 주어진 State와 Action으로 다음 State를 정확히 예측할 수 있다면 연쇄적으로 수행하여 Multi-Step 이후에 대해서도 정확히 예측할 수 있다. 하지만 현실적으로 One-Step Prediction으로 Multi-Step Prediction을 정확히 수행하는 것은 어려운데, PlaNet에서는 Latent OverShooting을 적용하여 이러한 문제를 해결하려고 한다.

Multi-Step Predictive Distribution

$d$ 시점 이후의 State를 예측하도록 Lower Bound 식을 정리하면 다음과 같다. 편의상 $a_{< t}$ 는 모두 생략했으며, 식의 모든 $s_t$ 는 $a_{< t}$ 에 따라 결정된다.

\eqalign{ \log p_d (o_{1:T}) \geq& \Sigma_{t=1}^T (E_{q(s_t \lvert o_{\leq t})}[\log p(o_t \lvert s_t)])\\ &- E_{p(s_{t-1} \lvert s_{t-d})q(s_{t-d} \lvert o_{\leq t-d})}[\text{D}_{\text{KL}}[q(s_t \lvert o_{\leq t}) \lvert \rvert p(s_t \lvert s_{t-1})]] }

위의 식과 One-Step Prediction 식의 차이는 $E_{q(s_{t-1} \lvert o_{\leq t-1}, a_{< t-1})}$ 이 $E_{p(s_{t-1} \lvert s_{t-d})q(s_{t-d} \lvert o_{\leq t-d})}$ 로 바뀌었다는 점에 있다. 기존에는 $t-1$ 시점에서 얻을 수 있는 정보들로 $t$ 시점을 예측했다면 Multi-Step이 되면서 $t-d$ 시점에서의 정보가 담겨있는 $s_{t-d}$ 로 $t$ 시점을 예측하게 되었다.

이렇게 바뀌면서 단순히 Multi-Step 이후를 예측한다는 것 뿐만 아니라 $t-d$ 시점과 $t$ 시점 사이에 추가적인 Observation 없이도 예측이 가능해졌다는 점이 중요하다. 즉 중간의 Observation 없이 Multi-Step 이후의 Latent State를 예측하는 것이 가능하다는 것이다.

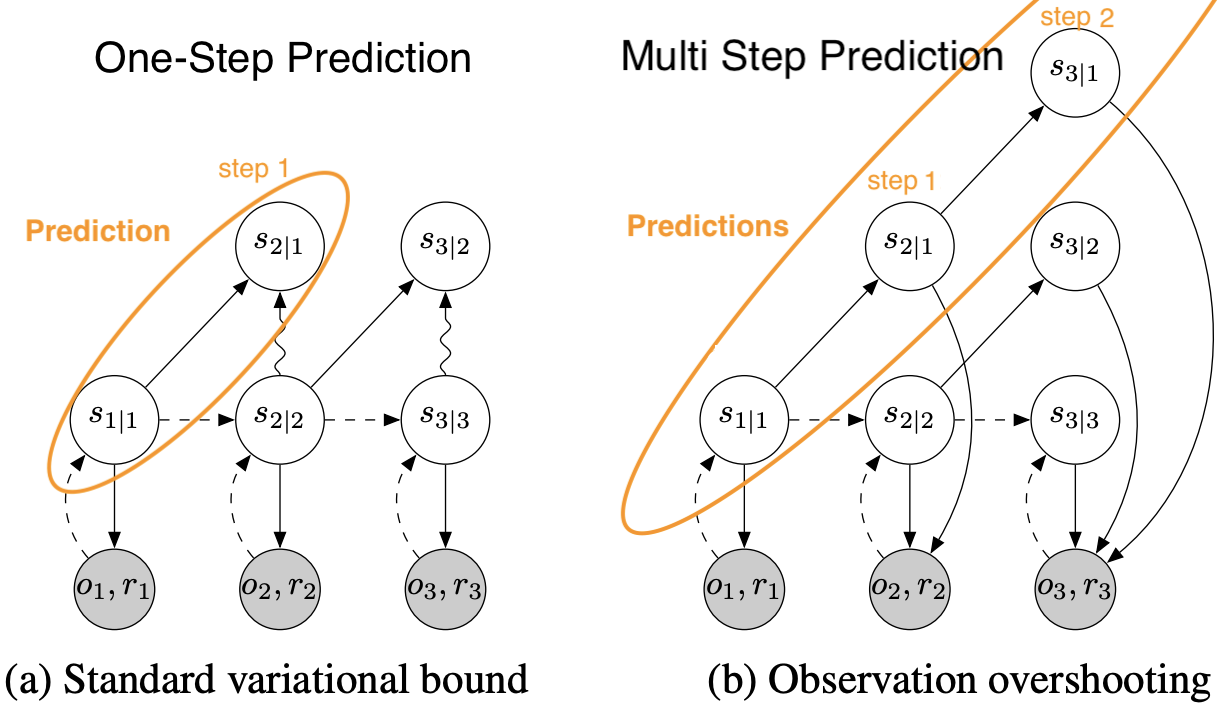
위의 그림에서 확인할 수 있듯이 위의 식은 예측한 Latent State가 얼마나 정확한지 확인하기 위해 실제 Observation과의 Reconstruction Error를 구하게 된다.

E_{q(s_t \lvert o_{\leq t})}[\log p(o_t \lvert s_t)]

이러한 점에서 이 방법을 Observation OverShooting 이라고 한다. 그런데 이렇게 되면 매번 예측 Latent State를 복원해야 한다는 문제점이 생긴다. 게다가 $d$ 가 고정적이므로 다양한 Multi-Step에 대한 자유로운 예측도 어렵다는 문제점이 있다.

Latent OverShooting

Latent OverShooting에서는 이러한 문제를 해결하기 위해 다음과 같이 식을 변경하게 된다.

\eqalign{ {1 \over D} \Sigma_{d=1}^D \log p_d (o_{1:T}) =& \Sigma_{t=1}^T (E_{q(s_t \lvert o_{\leq t})}[\log p(o_t \lvert s_t)])\\ &- {1 \over D} \Sigma_{d=1}^D \beta_d E_{p(s_{t-1} \lvert s_{t-d})q(s_{t-d} \lvert o_{\leq t-d})}[\text{D}_{\text{KL}}[q(s_t \lvert o_{\leq t}) \lvert \rvert p(s_t \lvert s_{t-1})]] }

논문에 나와있는 이미지로 식의 의미를 이해하면 다음과 같다.

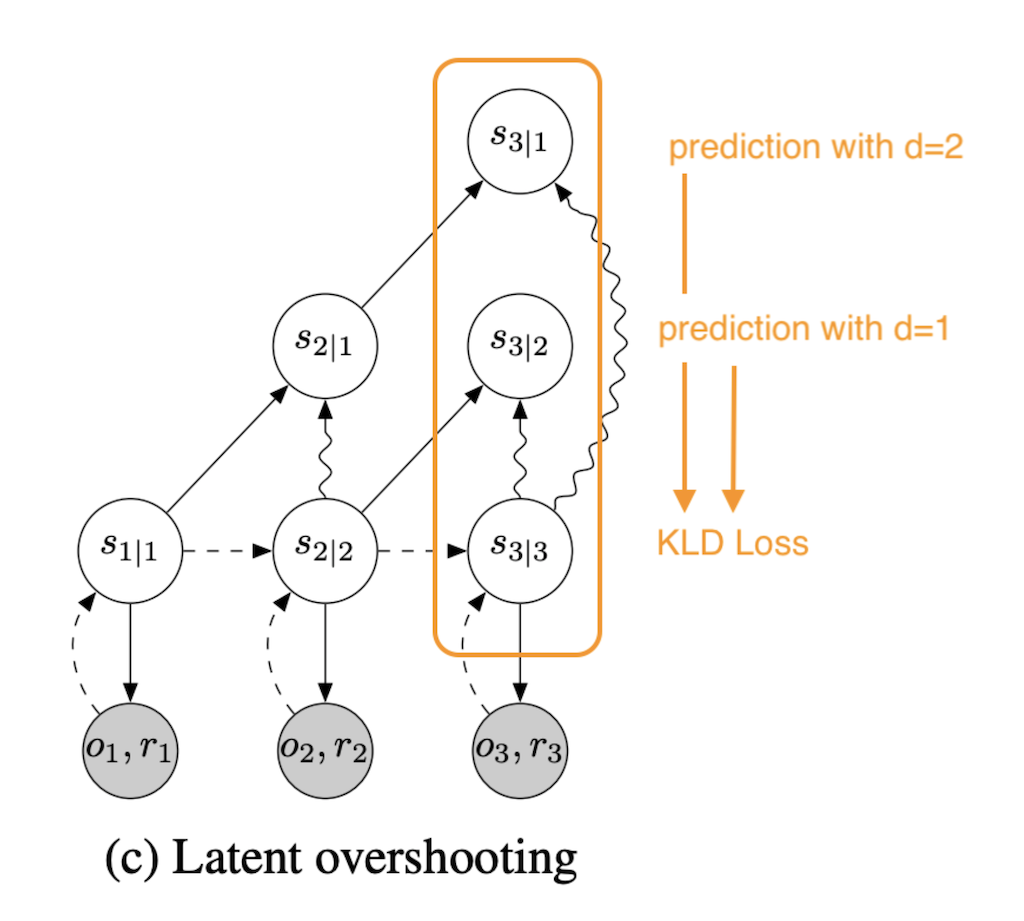
Latent OverShooting에서는 $t$ 시점에 접근 가능한 모든 Distance $d$ 의 Latent State를 $s_t$ 와의 비교를 통해 학습을 진행하도록 하고 있다. 따라서 Latent State를 Reconstruction 할 필요가 없고, 여러 Distance에 대해 일괄적으로 처리할 수 있다는 장점을 가지고 있다. 위의 식에서 $\beta$ 는 $\beta$ -VAE를 말한다.

Algorithm

전체 알고리즘은 다음과 같다. 11번째 줄에서 $\text{planner}$ 가 위의 Take Action with Planning Algorithm에서 확인한 Planning 알고리즘이다.

Data Collection

Environment의 Dynamics를 정확하게 학습하기 위해서는 다양한 State-Action에 대해 경험하는 것이 중요하다. 그런데 Agent가 처음부터 모든 State를 방문하는 것은 대부분의 환경에서 불가능하며, Policy가 업데이트되면서 쉽게 방문할 수 있는 State 또한 달라지게 된다. 강화학습의 이러한 특성을 반영하여 PlaNet은 학습이 이뤄질 때마다 새로운 Episode를 Dataset에 추가하며, 이때 다양한 경험을 위해 매 Episode마다 Seed를 바꿔준다. 그리고 Planning Horizon을 줄이고, Action의 효과를 정확하게 반영하기 위해 Action을 $R$ 번 반복한다. 알고리즘 상에서는 13번째 줄에서 다음과 같이 표현된다.

\eqalign{ &\text{for action repeat } k = 1...R \text{ do}\\ & \qquad r_t^k, o_{t+1}^k \leftarrow \text{ env.step} (a_t) }