Enfow's Blog

Scott Fujimoto, David Meger 등
2019
paper link

Summary

batch setting에서 일반적인 off-policy를 통해 학습하게 되면 extrapolation error로 인해 성능이 잘 나오지 않는다.
extrapolation error란 현재 policy가 선택하는 (s,a)의 분포와 batch 내에 저장된 (s,a) 분포 간의 차이로 인해 발생하는 문제이다.
BCQ 알고리즘에서는 이러한 문제를 해결하기 위해 VAE를 이용해 next state $s'$ 에서 batch 내의 transaction과 유사한 action $a'$ 을 선택할 수 있도록 하여 이러한 문제를 해결한다.

Batch reinforcement learning

Batch RL은 더 이상 환경과의 상호작용 없이 고정된 데이터셋을 통해서만 강화학습 모델을 학습시키는 방법이다. 현실적으로 환경의 반응을 얻는 것이 비싸고, 위험하며 시간이 오래 걸리는 경우가 많은데 Batch RL은 이러한 문제를 해결하기 위한 방법으로 제시되었다. 이와 유사한 문제를 해결하기 위한 방법으로 expert의 policy를 학습하는 imitation learning이 있지만, suboptimal에 빠지는 문제 등으로 인해 실패하는 경우가 많았다. 반면 batch RL은 데이터셋 자체의 질(quality)에 대한 제한이 없기 때문에 imitation laerning의 문제점이 다소 해소되는 측면이 있다.

Batch RL 또한 오랫동안 연구되어온 강화학습 분야 중 하나이지만, 특별한 방법 없이 단지 replay buffer만 저장하고 이를 데이터셋으로 활용하는 방법은 성공하지 못했다. 이와 관련하여 논문에서는 Batch RL에서 학습이 잘 이뤄지지 않는 원인이 extrapolation error이라는 것을 밝힌다. 그리고 이를 극복하기 위한 방법으로 batch-constrained reinforcement learning을 소개하며, 구체적인 알고리즘으로 Batch-Constrained deep Q-learning(BCQ)를 제시한다.

Extrapolation Error

Batch를 이용하여 off-policy 알고리즘을 학습시키는 것이 실패하는 원인으로 데이터셋과 현재 policy 간에 차이가 많기 때문이라고 한다. 이를 보다 정확하게 설명하기 위해 논문에서는 extrapolation error라는 개념을 도입하고 있다. extrapolation error는 batch에 저장된 data를 뽑아내는 데 사용된 Policy와 현재 학습 대상이 되는 Policy 간에 차이로 인해 발생하며, 이는 value function(current policy)이 선택하는 action에 대해 batch 내에 유사한 state-action 조합이 존재하지 않는 경우에는 정확한 target value를 측정하지 못하는 문제로 이어지게 된다.

off-policy & Extrapolaction error

그렇다면 왜 on-policy에서는 문제가 적고 off-policy에서 문제가 커지게 될까. 그 이유를 생각해보기 위해 on-policy의 쉬우면서도 대표적인 모델인 Deep SARSA를 DQN 알고리즘과 비교해보자.

\text{DQN} : Q(s,a) = Q(s,a) + \alpha(R + \gamma \max Q(s',a') - Q(s,a)) \\ \text{SARSA} : Q(s,a) = Q(s,a) + \alpha(R + \gamma Q(s',a') - Q(s,a))

알고리즘 수식적으로 볼 때 DQN에는 target value를 구하는 데 max operator를 사용하지만, Deep SARSA에서는 그렇지 않다는 점이 다르다. 즉 SARSA와 같은 on-policy 알고리즘에서는 q value가 가장 큰 action을 선택하는 것이 아니라 replay buffer에 저장된 action a'을 그대로 사용한다. 따라서 off-policy에서는 buffer에 저장되는 transaction이 (s, a, r, s')이 되지만 on-policy에서는 (s, a, r, s', a')가 저장된다.

replay buffer가 이렇게 구성되면 어떤 next state $s'$ 과 next action $a'$ 조합과 동일한 state $s$ , action $a$ 가 항상 존재하기 때문에 학습이 가능해진다. 왜냐하면 replay buffer에서 다음에 저장되는 transaction의 state와 action이 이전 transaction의 next state, next action과 동일하기 때문이다. 반면 off-policy에서는 next state $s'$ 에서 결정되는 next action $a'$ 이 다음 transaction과는 무관하다. 따라서 Extrapolaction Error가 보다 심각해진다.

Extrapolation error의 원인

구체적으로 논문에서는 다음 세 가지를 extrapolation error의 원인으로 제시하고 있다.

1. Absent data

정확하게 target value를 측정하기 위해서는 $Q_\theta(s', \pi(s'))$ 를 정확하게 구할 수 있어야 한다. 하지만 Batch 내에 $(s', \pi(s'))$ 의 조합과 동일한 또는 유사한 transaction이 존재하지 않는다면 그에 대한 학습이 이뤄지지 못해 그 값 또한 정확하게 측정하기 어렵다는 문제가 있다.

2. Model Bias

기본적인 MDP 모델에서는 무한의 state-action visitation을 가정한다. 하지만 데이터셋에 저장된 state-action 만 사용 가능한 경우 그 분포에 있어 차이가 있을 수 밖에 없다.

3. Training mismatch

현재의 policy가 가지고 있는 분포와 batch 내의 데이터가 가지고 있는 분포가 다른 경우 policy가 선택하는 action에 대해서는 학습이 많이 이뤄지지 못해 값을 정확하게 구하는 것이 어렵다.

Extrapolation 실험

off-policy에서는 현재의 policy와 상관성이 높은 데이터들이 buffer에 저장되고 학습에 사용되게 된다. 그렇다면 상관성이 낮은 데이터를 이용해 off-policy 알고리즘을 학습시키는 경우 어떻게 될까. 이를 알아보기 위해 논문에서는 Hopper-v1 환경에서 다른 DDPG(behavior DDPG)에 의해 만들어진 buffer로 DDPG 모델을 학습시켜(off-policy DDPG) 성능 등을 비교해보는 방법으로 실험을 진행했다. 실험의 결과부터 이야기하면 buffer와의 상관성이 낮은 off-policy DDPG의 성능이 상관성이 높은 behavior DDPG보다 성능이 크게 낮았다. 이러한 결과를 바탕으로 논문에서는 기존의 순수한 off-policy 알고리즘을 Batch RL에 바로 적용하는 것에는 어려움이 있다고 이야기한다.

실험 셋팅 중 가장 중요한 것은 buffer(dataset)를 어떻게 얻을 것인가에 관한 것으로 논문에서는 다음 세 가지 방법을 사용했다고 한다. 첫 번째는 Gaussian noise를 다소 크게 부과하여 탐색의 정도를 높인 DDPG모델로 100만 step 동안 축적한 최종 buffer를 그대로 저장하여 off-policy 모델을 학습하는데 사용하는 방법이다. 최종적으로 저장된 buffer를 batch로 사용한다는 점에서 final buffer 방법이라고 한다. 두 번째는 상대적으로 낮은 Gaussian noise를 가지고 있는 behavior에 의해 buffer가 축적되는 과정에 off-policy 모델이 함께 학습되는 방법이다. 이 방법의 경우 behavior와 off-policy 모델이 완전히 동일한 buffer로 학습한 것이 된다. 동시에 학습하므로 Concurrent 방법이라고 한다. 마지막 세 번째는 imiation learning 방법이라 이름 붙인 것으로, 이미 완전히 학습된 DDPG가 고정된 채로 100만 step 동안 쌓은 buffer를 사용하여 off-policy 모델을 학습하는 방법이다.

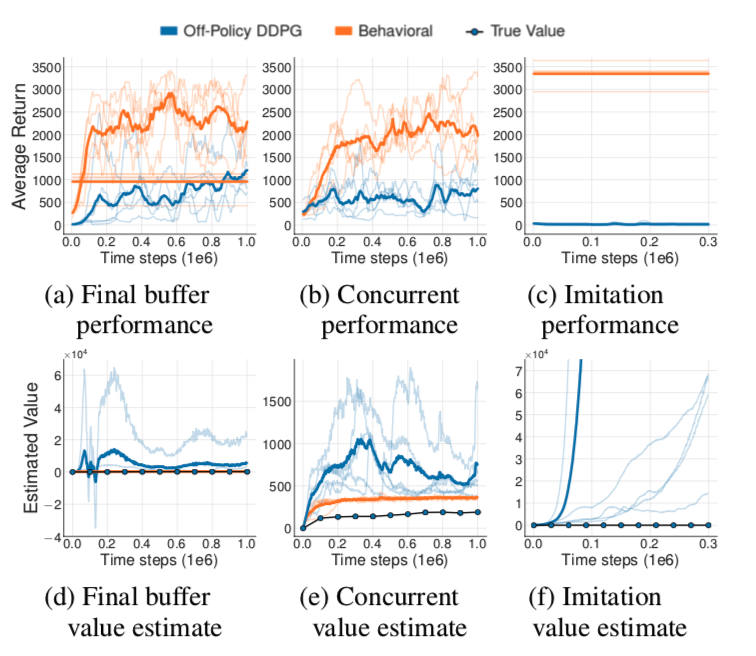
실험을 결과를 보면 세 가지 모든 경우에서 behavior 모델보다 off-policy 모델의 성능이 좋지 않았다. 특히 두 번째 경우와 같이 동일한 buffer를 이용해 학습이 이뤄진 경우에도 잘 되지 못했는데, 이러한 점에서 policy의 초기값(initial policy) 간의 차이 정도만으로도 exploratione error가 발생하여 학습이 되지 않는다는 것을 알 수 있다.

게다가 MuJoCo 환경이 아닌 실제 환경에서는 state와 action 등의 차원이 크기 때문에 복잡도가 높고, 그에 따라 데이터셋이 아무리 크다고 할지라도 catastrophic forgetting 문제가 발생할 가능성이 있다. 따라서 단순히 데이터셋을 늘리는 방법으로 위에서 언급한 extrapolation error 문제를 해결하는 것도 어렵다.

Batch Constrained Reinforcement Learning(BCQ)

extrapolation error를 줄이기 위해서는 $s'$ 를 이용해 target value를 구할 때 batch 내에 저장되어 있는 $(s,a)$ 조합과 유사한 action을 선택해야 한다. 즉, off-policy agent는 데이터가 존재하는 영역에 대해서는 정확하게 value를 결정할 수 있기 때문에 batch에 저장된 영역에 대해서만 학습을 진행하는 것이 안전하다. BCQ 알고리즘에서는 이러한 점을 이용하기 때문에 batch-constrained라는 표현이 등장한다.

보다 구체적으로 batch 환경에서 off-policy agent를 안정적으로 학습시키기 위해서는 action을 선택하는데 있어 다음 세 가지 조건이 요구된다.

batch에 저장된 데이터와 선택된 action 간의 거리가 최소화되어야 한다.
익숙한 데이터가 많은 방향으로 state가 결정되도록 한다.
value function을 극대화한다.

이들 조건 중 첫 번째 조건에 대해서는 위에서 다수 언급했었다. 하지만 첫 번째 조건이 만족된다고 할지라도 두 번째와 세 번째 조건이 만족되는 것은 아니기 때문에 단순히 거리가 가장 작은 action을 선택하는 것만으로는 부족하다. 남은 두 가지 조건을 만족시키기 위해서는 batch에 저장된 전체 transition에 대해 알고 있어야 한다. 따라서 이러한 문제를 해결하기 위해 논문에서는 생성 모델(generative)을 도입하고 있다.

BCQ algorithm

Generative model in BCQ

BCQ에 생성모델을 도입한 이유는 명료한데, batch에 있을 법한 action을 선택하는 것이다. 따라서 생성모델의 입력값은 next state $s'$ 이 되고, 출력값은 next action $a'$ 이 된다. 그리고 이때 action은 batch의 그것과 유사해야 하므로, 생성모델을 학습시킬 때에는 batch의 데이터들을 활용한다.

논문에서는 이를 수학적으로 표현하기 위해 similarity metric으로 $P_B^G(a\|s)$ 를 도입하고 있는데, 어떤 $(s, a)$ pair와 batch $B$ 에 저장된 state-action pair 간의 유사도를 state-conditioned marginal likelihood로 표현한 것이다. $P_B^G(a\|s)$ 를 극대화하게 되면 어떤 state가 주어졌을 때 batch에 저장된 것과 유사한 action이 나오게 된다. 하지만 만약 state가 고차원에 연속적이라면 이를 추정하는 것 또한 쉽지 않다. 이러한 이유로 이를 극대화할 수 있는 생성 모델을 별도로 도입하는 것이라고 할 수 있다.

생성모델로는 VAE를 사용하고 있다.

Perturbance model

생성모델의 출력값을 곧바로 사용하는 것이 아니라 perturbance를 추가해주는 term을 덧붙여 action 값이 일정 범위 내에서 다양하게 결정되도록 한다. perturbance model $\xi_{\varnothing}(s, a, \Phi)$ 또한 학습 대상이 된다. 이때 action의 조정 범위는 $[-\Phi, \Phi]$ 가 된다.

Perturbance model은 DPG 방법을 이용하여 Q 값을 극대화하는 방향으로 업데이트된다.

generative model과 perterbance model로 구성된 policy $\pi$ 는 다음과 같다.

\pi(s) = argmax_{a_i + \xi_{\varnothing}(s,a_i,\Phi)} Q_\theta(s,a_i + \xi_\varnothing(s, a_i, \Phi)), \\ { \{a_i - G_\omega (s) \} }_{i=1}^n

위 식에서 $n$ 은 하나의 next state $s'$ 에서 후보로 선택된 next action $a'$ 의 개수를 말한다. 그리고 perturbance model의 $\Phi$ 는 next action $a'$ 이 선택되는 범위를 제한한다. 이 두 가지 hyperparameter는 강화학습 알고리즘과 imitation laerning 알고리즘 간의 상충관계를 형성한다. 만약 $\phi = 0$ 이고, $n=1$ 이라면 Behavior cloning과 유사하게 동작한다. 반면 $\Phi \rightarrow a_{max} - a_{min}$ , $\ n \rightarrow \infty$ 라면 Q-learning과 비슷해진다.

perturbance model을 업데이트하기 위해 DPG 방법을 사용한다고 했었는데, 구체적인 알고리즘은 다음과 같다.

\varnothing \leftarrow argmax_\varnothing \sum_{(s,a) \in B} Q_\theta(s,a+\xi_\varnothing(s,a,\Phi)) \\ a - G_\omega(s)

Clipped Double Q-learning

안정적인 업데이트를 위해서 두 개의 Q network를 학습하고 둘 중 작은 값을 선택하는 Clipped Double Q-learning 알고리즘을 적용하였다. Clipped Double Q-learning은 원래 Overestimation error를 줄이기 위한 방법으로 제시되었지만, BCQ에서는 minimum operator가 불확실성이 높은 영역에서 variance가 높은 것에 패널티를 부과하기 때문에 policy가 batch 내에 있는 state로 가는 action을 선호하도록 만들어주는 효과 또한 있다고 한다.

Clipped Double Q-learning을 적용해 BCQ에서 target value를 구하는 식은 다음과 같다.

r + \gamma \max_{a_i} \lbrack \lambda \min_{j = 1,2} Q_{\theta'_j}(s', a_i) + (1 - \lambda) \max_{j=1,2} Q_{\theta'_j}(s', a_i) \rbrack

일반적인 Clopped Double Q-learning 알고리즘과의 차이는 min operator와 max operator의 값을 가중평균하고 있다는 점이며, 이때 min operator의 값의 비율이 $\lambda$ 로 조정된다. 만약 $\lambda = 1$ 이면 Clipped Double Q-learning과 동일하게 업데이트 되는 것이다. min operator가 불확실성을 다루는 것과 연관되는 만큼 $\lambda$ 값을 높게 잡으면 불확실한 state로 가는 것을 더 크게 제한하는 것으로 받아들일 수 있다.