Enfow's Blog

Sergey Ioffe, Christian Szegedy
2015
논문 링크

Summary

Internal Covariate Shift란 이전 레이어의 파라미터 변화로 인해 이후 레이어들의 입력값의 분포가 변화하는 것을 말한다.
Batch Normalization은 입력값의 분포를 조정하여 Internal Covariate Shift로 인한 문제, 느린 학습 속도, Gradient Vanishing 문제를 해결한다. Normalizing은 데이터 포인트의 개별 변수를 대상으로 진행한다.
Training Time에는 Mini-Batch에 포함된 데이터 포인트들로 평균과 분산을 구하고, Inference Time에는 안정적인 Inference를 위해 각 Mini-Batch의 평균과 분산을 이용하여 모든 데이터 포인트에 일괄적으로 적용되는 평균과 분산을 구한다. 선형 변환을 수행하는 $\beta, \gamma$ 는 Learnable 파라미터이다.

Internal Covariate Shift

딥러닝 모델들은 기본적으로 복수의 Layer를 가지고 있으며 입력층을 제외한 은닉층과 출력층은 이전 레이어의 출력값을 입력값으로 받는다. 조금 더 정확하게 말하면 이전 레이어들의 파라미터에 영향을 받게 되고 이들이 바뀔 때마다 입력값의 분포 자체가 변하게 된다. 이는 학습이 진행될 때마다 입력값 분포의 변화에 끊임없이 적응해야 하도록 만들어 딥러닝 모델의 안정적인 학습을 저해하는 요인이 된다.

논문에서는 이러한 문제, 즉 레이어의 입력값의 분포가 계속해서 변화하는 문제를 Internal Covariate Shift라고 부른다. Covariate Shift는 공변량 변화 정도로 번역되며 Dataset Shift의 일종으로서 입력 값의 분포가 변화하는 문제를 지칭한다. 여기서는 Covariate Shift이기는 한데, 모델 전체의 입력값이 아니라 모델 내부의 레이어 또는 서브 네트워크의 입력값에서 발생한다는 점에서 Internal이라는 표현이 붙은 것이다. 원문의 정의는 다음과 같다. 참고로 여기서 Network Activations는 레이어의 입력값들이라고 생각하면 된다.

"We define Internal Covariate Shift as the change in the distribution of network activations due to the change in network parameters during training"

Internal Covariate Shift 문제는 단순히 각 레이어가 새로운 분포를 계속 학습해야 한다는 것 외에도 Sigmoid Activation Function과 관련해 주로 발생하는 Seturating Problem과 Gradient Vanishing Problem을 심화하는 문제도 안고 있다. 즉 이전 레이어의 변화로 입력값의 분포가 변화하는 와중에 그림과 같이 Activation Function의 Gradient가 거의 0인 지점에 들어가게 되면 다시 빠져나오기 어렵다는 것이다.

\text{Sigmoid: } a(x) = {1 \over e^{-x} + 1}

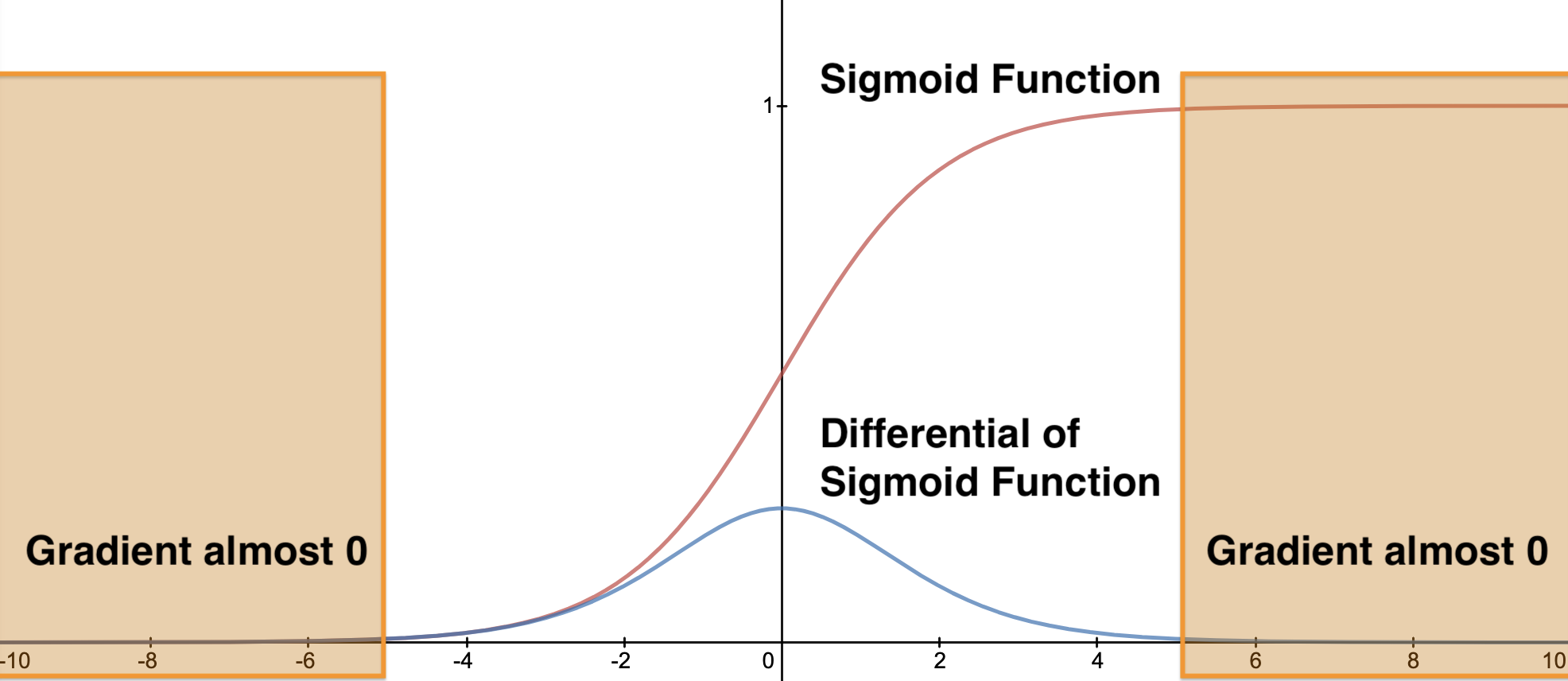
물론 이에 대한 해결책으로 다음과 같이 다양한 방법들이 제시되어왔다.

ReLU(Rectified Linear Units)
Carefule Initialization
Small Learning Rate

하지만 Activation function의 입력값의 분포가 안정적이라면 보다 빠른 학습이 가능할 것이라는 점에서 Internal Covariate Shift를 해결하는 것이 중요하다. Batch Normalization에서는 직접적으로 Internal Covariate Shift를 줄이는 것을 시도한다.

Batch Normalization

Batch Normalization의 목표는 각 레이어의 입력값의 평균과 분산을 고정하여 딥러닝 네트워크의 학습속도를 높이는 것이다. 세부적으로 논문에서 제시하는 Batch Normalization의 장점은 다음과 같다.

학습속도가 빨라진다.
Dropout를 사용하지 않아도 된다.
Sigmoid 계열의 Activation Function도 사용할 수 있다.
Gradient가 파라미터의 스케일에 영향을 받지않아 보다 큰 learning rate가 가능하다.

그런데 Batch Normalization 이전에도 평균과 분산을 0, 1로 고정하여 네트워크의 학습 속도를 높이는 방법론이 제안되었는데, LeCun의 Whitening Transformation이 대표적이다.

Whitening Transformation

Whitening Transformation이란 전처리의 일종으로 데이터의 변수 간에 존재하는 Correlation을 없애고 분산을 1로 맞추는 작업을 말한다. 입력 데이터를 White Noise Vector로 만든다는 점에서 Whitening Transformation 이라고 한다(Quora).

그러나 Whitening을 레이어 입력값마다 적용하는 것은 현실적으로 어렵다. 이유는 크게 두 가지인데 첫 번째는 전체 데이터셋의 데이터 포인트들을 함께 고려해야 하기 때문이고, 두 번째는 Whitening은 Covariance 계산과 그에 대한 Inverse Square Root를 계산해야 하는데, BackPropagation 시에는 이에 대한 미분을 구해야 한다는 점에서 연산 비용이 매우 많이 들기 때문이다. 따라서 논문에서는 Batch Normalization을 고안하는데 있어 전체 데이터셋을 고려하지 않아도 되면서 쉽게 미분이 가능한지 고려했다고 한다.

Normalizing Each Dimension

Whitening Transformation과 Batch Normalization의 차이점으로는 다음 세 가지를 들 수 있다.

모든 변수가 서로 독립이라고 가정한다. 따라서 Decorrelation이 필요없다.
개별 변수마다 Normalize를 진행한다. 따라서 평균과 분산을 개별 변수 단위로 산출한다.
Mini-Batch 단위로 평균과 분산을 계산한다(Training).

따라서 $d$ 차원의 입력값 $\boldsymbol{x} = (x^{(1)}, ..., x^{(d)})$ 이 주어졌을 때 각각에 대해 다음과 같이 Normalize하게 된다.

\hat x^{(k)} = { x^{(k)} - E[x^{(k)}] \over \root \of {\text{Var}[x^{(k)}]}}

즉 레이어의 입력값을 다음과 같이 전처리하게 되면 데이터의 분포를 일정하게 유지할 수 있다. 하지만 이를 바로 적용하게 되면 몇 가지 문제점이 발생한다. 대표적인 것이 평균과 분산이 0, 1로 고정되는 경우 Sigmoid Function의 Non Linear Function으로서의 특성이 줄어든다는 점이다. 아래의 이미지를 보면 보다 확실한데 0 주변에서는 Sigmoid가 선형 함수인 $y=0.225x + 0.5$ 와 매우 유사함을 알 수 있다.

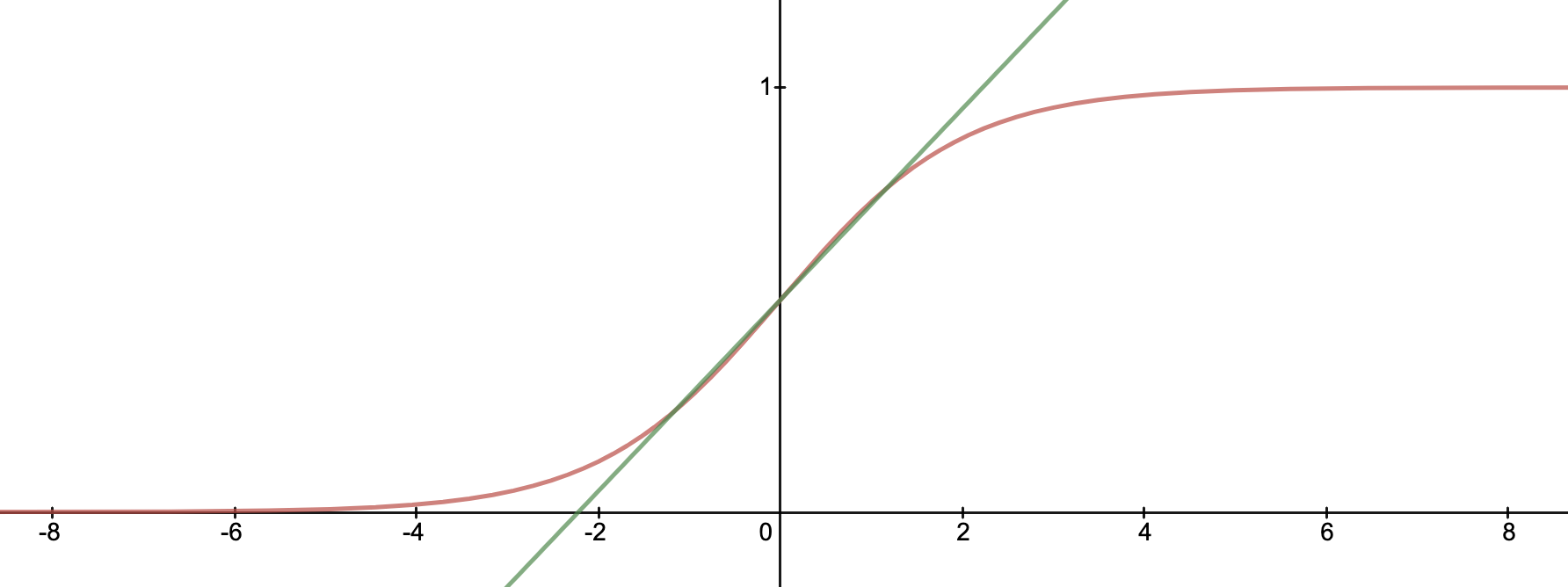
이러한 문제를 해결하기 위해서 Batch Normalization에서는 Normalizing 함수 뒤에 필요에 따라 Shifting과 Scaling이 가능하도록 Linear Transformation을 붙이게 된다. 즉 필요하다면 원 분포대로 복원할 수 있도록(identity transform) 하겠다는 것이다.

y^{(k)} = \gamma^{(k)} \hat x^{(k)} + \beta^{(k)}

여기서 Scaling을 가능하게 하는 $\gamma^{(k)}$ 와 Shifting을 가능하게 하는 $\beta^{(k)}$ 는 모두 Learnable Parameter이며,

\eqalign{ &\gamma^{(k)} = \root \of {\text{Var}[x^{(k)}]} \\ &\beta^{(k)} = E[x^{(k)}] }

로 설정하면 Identity Transform이 된다는 것을 알 수 있다.

Normalizing via Mini-Batch Statistics

Batch Normalization은 Normalization을 할 때 사용하는 평균과 분산을 Mini-Batch를 단위로 계산한다. 즉

\hat x^{(k)} = { x^{(k)} - E[x^{(k)}] \over \root \of {\text{Var}[x^{(k)}]}}

에서 $E[x^{(k)}]$ 와 $\text{Var}[x^{(k)}]$ 는 전체 데이터셋의 $x^{(k)}$ 가 아니라 Mini-Batch의 $x^{(k)}$ 로 구한 평균과 분산이다. 따라서 Batch Normalization의 출력 값은 입력값 외에도 Mini-Batch로 함께 들어온 다른 입력값들의 영향을 받는다고 할 수 있다. 이러한 점 때문에 Inference Time에는 다른 방법을 사용하게 된다.

Mini-Batch Statistics을 사용하는 Batch Normalization Transform 알고리즘은 아래와 같다.

그리고 Mini-Batch의 크기가 $m$ 이라고 했을 때 각각의 Gradient는 Chain Rule에 따라 다음과 같이 구해진다. 즉 Batch Normalization Transform은 미분 가능하며 모든 파라미터들인 Back Propagation에 따라 업데이트된다.

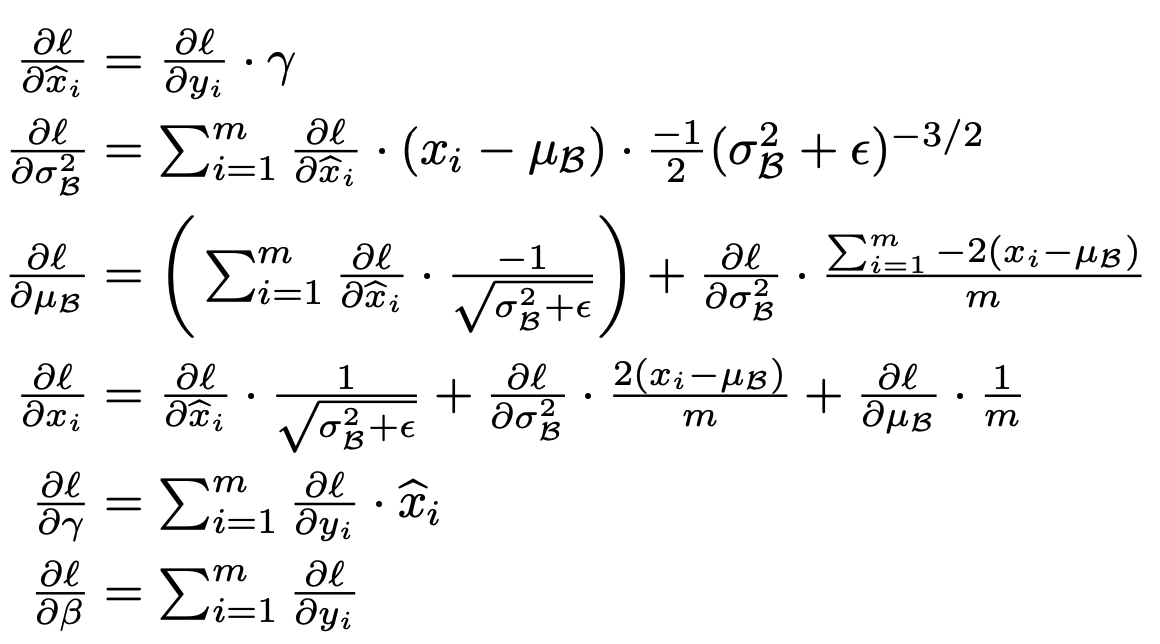
Difference between Train Time and Inference Time

앞에서 언급한대로 Batch Normalization의 출력값은 입력값 외에도 Mini-Batch로 함께 들어온 다른 입력값들의 영향을 받는다. 그런데 Inference Time에도 함께 들어온 다른 입력값들에 의해 출력값이 달라지면 출력값이 안정적이라고 할 수 없다. 즉 Inference 시에 출력값은 오로지 입력값에 의해서만 결정되어야 한다.

이를 위해 Inference Time에는 $E[x]$ 와 $\text{Var}[x]$ 를 Mini-Batch의 평균으로 구하지 않고, Train Time에 구한 각 Mini Batch의 평균을 구하여 모든 Inference 데이터 포인트에 일괄적으로 적용한다. 구체적인 식은 다음과 같다.

\eqalign{ E[x] &= E_{\mathcal B} [\mu \mathcal B]\\ \text{Var}[x] &= {m \over {m - 1}} E_{\mathcal B} [\sigma^2_{\mathcal B}] }

아래 알고리즘을 보면 Batch Normalization이 적용되는 과정을 알 수 있다.

line 2,3,4: 각 Layer마다 Batch Normalization Transformation 적용
line 6: 모델의 파라미터 $\theta$ 와 Batch Normalization의 파라미터를 함께 업데이트
line 10: Inference Time에 사용할 평균과 분산 계산
line 11: Inference Batch Normalization Transform 적용