Published on

[MAML] Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks

  • Chelsea Finn, Pieter Abbeel,Sergey Levine
  • 2017
  • Paper Link

Summary

  • MAML은 업데이트 알고리즘으로서, 복수의 Task가 공유하는 Internal Representation을 찾아 각각의 Task에 대한 Optimal Parameter에 보다 가까운 위치에서 업데이트를 시작할 수 있도록 해준다.
  • MAML은 Model-Agnostic, 즉 Model의 구조와 Task의 특성에 구애받지 않고 적용이 가능하다.
  • Parameter θ\theta의 업데이트 방향이 θ\theta를 기준으로 결정되는 것이 아니라, 어떤 Task TiT_i에 맞춰 업데이트 된 θi′\theta'_i를 기준으로 결정된다.

Learning New Task Quickly

Meta Learning의 목표는 적은 수의 데이터 만으로도 새로운 task를 학습하는 것이다. 이를 위해서는 과거의 경험을 토대로 적은 양의 정보를 학습하면서 동시에 새로운 데이터에 Overfitting 되는 것을 방지해야 하는데 결코 쉽지 않다. 논문은 이러한 문제의식에서 출발하며, 이를 위해 지도학습, 강화학습 등 학습 방법에 상관없이 Gradient를 통해 모델을 업데이트하기만 하면 모두 적용 가능한 Meta learning 방법론 **Model-Agnostic Meta-Learning(MAML)**을 제시한다.

Model-Agnostic Meta-laerning

새로운 Task를 적은 수의 데이터로 빠르게 학습하기 위해 Meta Learning은 새로운 Task와 유사한 Task들을 미리 학습하고, 여기에서 Task들이 가지는 공통의 Internal Representation을 추출하게 된다. 만약 새로 학습하고자 하는 Task가 이러한 Internal Representation의 특징을 상당부분 공유한다면 이미 Model이 해당 Task에 대한 사전 지식을 가지고 있는 상태라고 할 수 있으며, 이를 통해 약간의 Fine Tuning만으로도 좋은 성능을 낼 가능성이 높다.

Define Task

문제와 관련하여 논문에서는 Task TT를 다음과 같이 정의한다.

T={L(x1,a1,...,xH,aH),q(x1),q(xt+1∣xt,at),H}T = \{ L(x_1, a_1, ... , x_H, a_H), q(x_1), q(x_{t+1} \lvert x_t, a_t), H \}

각 구성요소가 의미하는 바는 다음과 같다.

NotationDescription
L(x1,a1,...,xH,aH)L(x_1, a_1, ... , x_H, a_H)Loss Function
q(x1)q(x_1)Initial Observation Distribution
q(xt+1∣xt,at)q(x_{t+1} \lvert x_t, a_t)Transition Distribution
HHEpisode Length

Supervised Learning 뿐만 아니라 Reinforcement Leanring 등 다양한 경우를 고려하기 위해 Transition Distribution을 포함하고 있다. i.i.d Condition을 가정하는 Supervised Learning이라면 H=1H=1이 되며, Initial Observation Distribution은 데이터의 분포가 된다. 이 경우 Transition Distribution은 사용하지 않는다.

Task가 위와 같이 정의된다면 학습하고자 하는 Task들의 분포는 p(T)p(T)로 정의할 수 있다. 그리고 학습 대상이 되는 개별 Task는 Ti∽p(T)T_i \backsim p(T)가 된다. 만약 K-Shot Learning이라고 한다면 TiT_i에서 정의하는 qiq_i에서 K개의 Sample을 추출하고, LTiL_{T_i}를 사용하여 Model을 업데이트하게 된다.

Prior Works

Meta Learning의 기존 방법으로는

  • 전체 Dataset을 학습하는 방법
  • Non-Parametric Method

가 대표적이다. 이 두 가지 방법론의 한계는 명확한데, 일반적으로 적용하는 데에 어려움이 있다는 것이다. Non-Parametric Method의 대표적인 예라고 할 수 있는 Vinyals의 Matching Network만 하더라도 분류 문제만을 목표로 삼고 있다. MAML은 임의의 p(T)p(T)에 맞춰 Parameter를 업데이트 하는 업데이트 알고리즘으로서 Model의 구조와 Task의 특성에 구애받지 않고 적용 가능하다는 점에서 이전의 방법론들과 차별적이다.

"Model-Agnostic"

MAML의 이러한 특성을 나타내는 단어가 MAML에서 Model-Agnostic이다. Model-Agnostic이란 학습에 사용된 모델이 무엇인지 상관없이 적용 가능하다는 것을 의미한다. 이름에 걸맞게 MAML은 Model의 구조에 어떠한 제약도 없으며, Model이 어떤 Parameter θ\theta로 Parametrized되어 있고, 이를 Loss Function이 충분히 Smooth하여 Gradient Descent(or Ascent)를 적용하여 Model을 업데이트 할 수 있기만 하면 적용이 가능하다. 이와 관련하여 논문에서는 Supervised Regression and Classification과 Reinforcement Learning 두 가지 케이스에 대해 적용 예시를 보여준다.

MAML is Parameter Update Algorithm

MAML은 여러 Task가 공유하는 Internal Representation을 찾아내는 방향으로 Model을 업데이트하는 방식에 관해 정의하는, 일종의 업데이트 알고리즘이다.

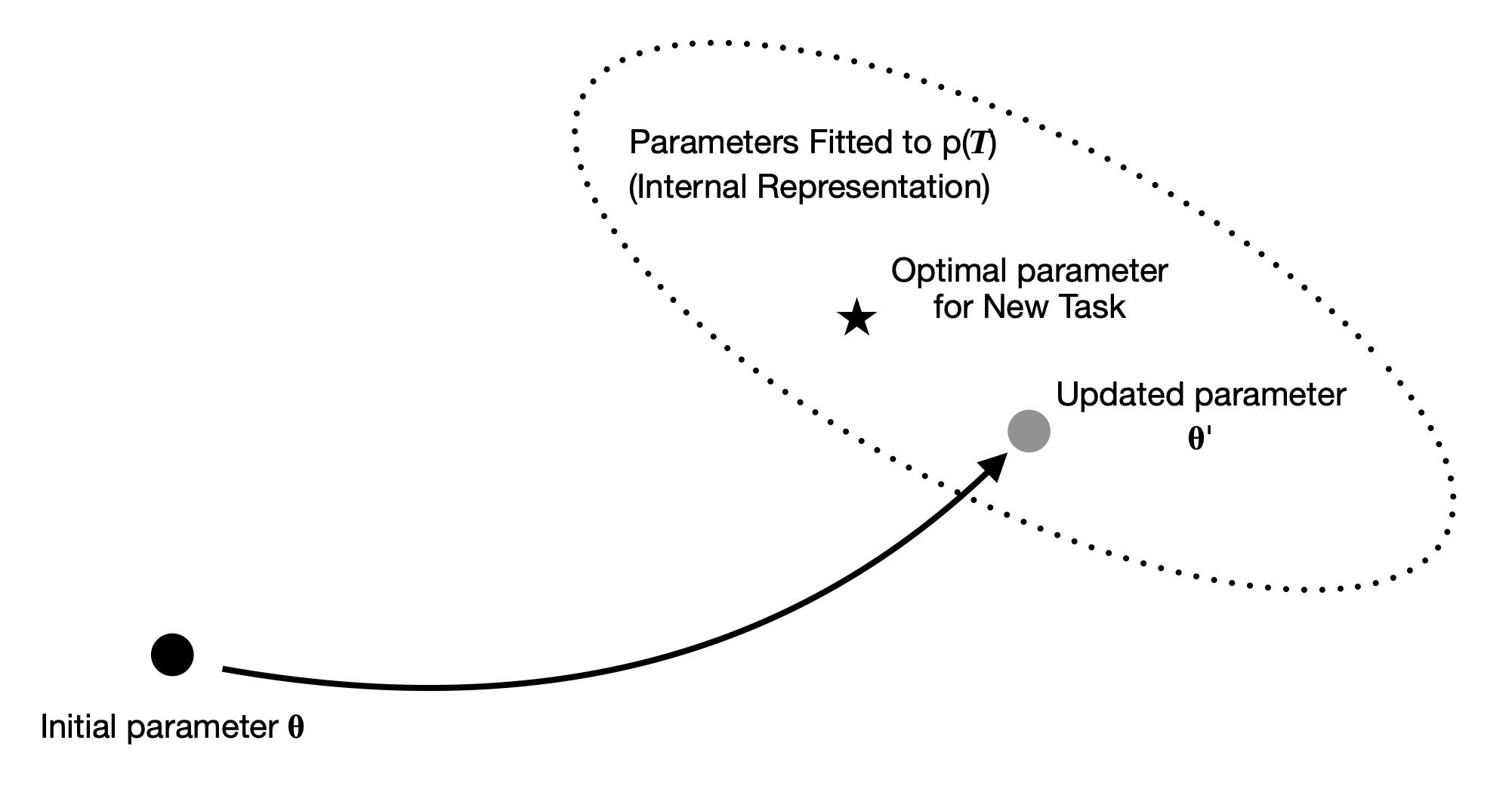
MAML에서 시도하는 접근방법은 위의 이미지와 같이 도식화 할 수 있다. 만약 일반적인 학습 방법대로 Initial Parameter θ\theta에 시작하여 새로운 Task를 학습한다면 상당히 많은 업데이트를 거쳐야 Optimal Parameter ⋆\star에 가까워질 수 있을 것이다. 하지만 MAML은 새로운 Task와 유사한 p(T)p(T)들에 맞춰 미리 Parameter를 업데이트하게 되고, 이렇게 업데이트 된 Parameter θ′\theta'에서부터 시작하게 된다. 따라서 새로운 Task에 대해 보다 적은 학습량 만으로도 충분히 Optimal Parameter ⋆\star에 도달하는 것이 가능하다.

How To Find θ′\theta'

그런데 θ′\theta'로 업데이트 하는 방법을 쉽게 찾을 수 있다면 좋겠지만 이를 구현하는 것은 쉬워보이지는 않는다. 이와 관련하여 논문에는 다음과 같은 표현이 나온다.

  • "We will aim to find model parameters that are sensitive to changes in the task, such that small changes in the parameters will produce large improvements on the loss function of any task drawn from p(T)p(T), when altered in the direction of the gradient of that loss"

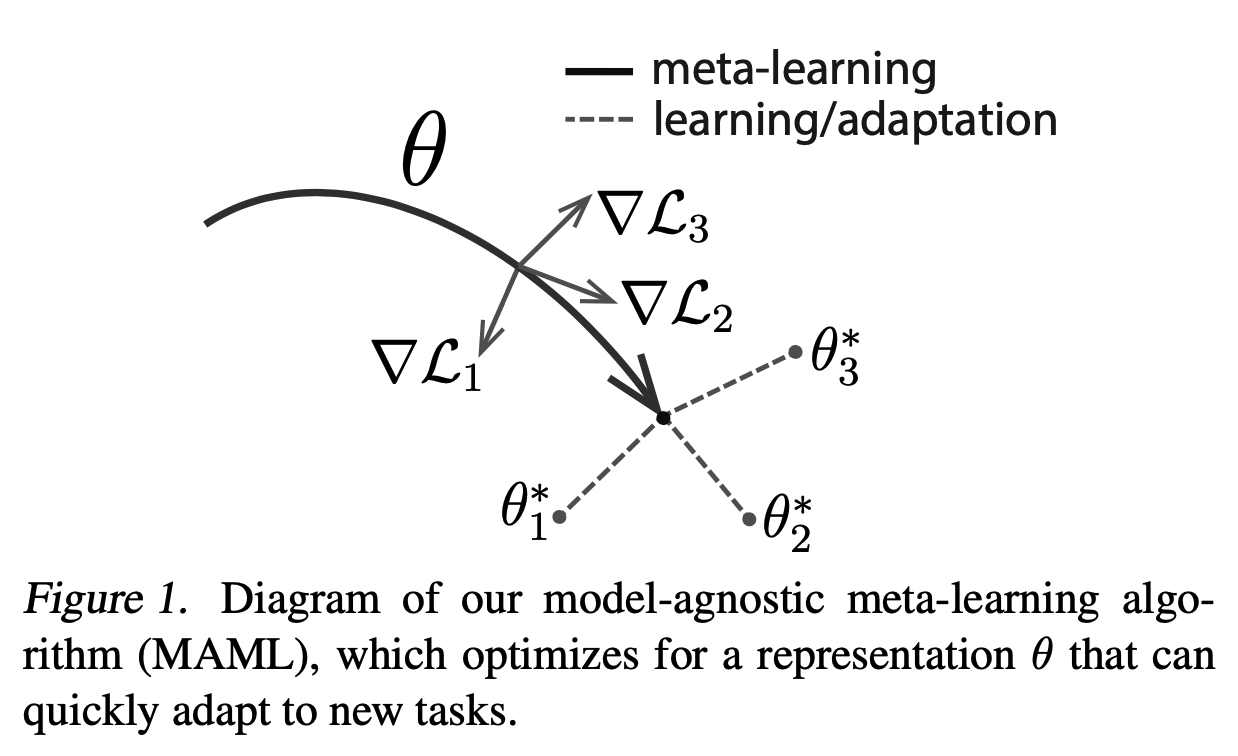
한마디로 각 Task가 가지는 loss function의 Gradient 방향으로 파라미터를 약간 업데이트 할 때, p(T)p(T)의 모든 Task들의 성능이 향상되는 파라미터 θ\theta를 찾겠다는 것이다. 아래 그림을 보게 되면 θ\theta가 업데이트 됨에 따라 점점 더 Task T1,T2,T3T_1, T_2, T_3의 Optimal한 θ1∗,θ2∗,θ3∗\theta_1^*, \theta_2^*, \theta_3^*에 가까워짐을 알 수 있다. 그리고 최종 θ\theta는 세 θ1∗,θ2∗,θ3∗\theta_1^*, \theta_2^*, \theta_3^* 어디에도 약간의 업데이트를 거쳐 도달할 수 있는 상태에 놓여 있다.

Parameter θ\theta로 Parameterized 된 모델을 fθf_\theta라고 하자. 만약 어떤 Task Ti∽p(T)T_i \backsim p(T)에 맞춰 θ\theta를 Gradient Descent에 따라 업데이트 한다면 다음과 같이 표현할 수 있다.

θi′=θ−α∇θLTi(fθ)\theta'_i = \theta - \alpha \nabla_\theta L_{T_i}(f_\theta)

만약 p(T)p(T)에서 샘플링할 수 있는 Task들에 대해 모두 적용한다면 다음과 같이 Meta-Objective를 정의할 수 있다.

min⁡θΣTi∽p(T)LTi(fθi′)=ΣTi∽p(T)LTi(fθ−α∇θLTi(fθ))\min_\theta \Sigma_{T_i \backsim p(T)} L_{T_i}(f_{\theta'_i}) = \Sigma_{T_i \backsim p(T)} L_{T_i}(f_{\theta - \alpha \nabla_\theta L_{T_i}(f_\theta)})

쉽게 말해 각각의 Task TiT_i에 맞춰 업데이트(Adaptation) 된 fθi′f_{\theta'_i}이 가지는 loss를 최소화하는 θ\theta를 찾는 것이 목표라는 것이다. 여기서 한 가지 특이한 점이 있다면 θ\theta에 대해서 업데이트하는데, 그 방향은 개별 Task TiT_i에 맞춰 한 번 업데이트 된 θi′\theta'_i들을 기준으로 결정한다는 것이다. 이것과 관련해서 나는 Test Time에서도 새로운 Task에 따라 θ′\theta'를 Adaptation한 뒤의 loss를 최소화하는 것을 목표로 한다는 것과 동일한 맥락으로 이해했다.

최종적으로 Objective Function에 맞춰 SGD를 적용한 업데이트 식은 다음과 같다.

θ←θ−β∇θΣTi∽p(T)LTi(fθ−α∇θLTi(fθ))\theta \leftarrow \theta - \beta \nabla_\theta \Sigma_{T_i \backsim p(T)} L_{T_i}(f_{\theta - \alpha \nabla_\theta L_{T_i}(f_\theta)})

그리고 이를 적용한 MAML의 기본 알고리즘은 다음과 같다.

Species of MAML

논문에서는 MAML의 가장 큰 장점으로 Model과 Task의 특성에 구애받지 않고 적용이 가능하다는 점을 들고 있다. 이를 확인하기 위해 논문에서는 대표적인 머신러닝 문제인 Supervised Regression and Classification과 Reinforcement Learning에 대한 적응 예를 직접 보여주고 있다. 각각의 경우에 대한 알고리즘은 아래와 같다.

Supervised Regression and Classification with MAML

Reinforcement Learning with MAML