논문 제목 : Scalable Distributed Deep-RL with Importance Weighted Actor-Learner Architectures

• Lasse Espeholt, Hubert Soyer, Remi Munos, Karen Simonyan, Volodymyr Mnih 등
• 2018
• 논문 링크
• PyTorch 구현 - Facebook torchbeast

Summary

• Actor에서 수집한 Trajectory를 Learner에게 곧바로 전달하여 Policy를 업데이트하는 알고리즘 IMPALA를 제시한다.
• Off-Policy의 Policy-Lag 문제를 해소하기 위해 도입한 V-Trace Target은 Truncated Importance Sampling 을 통해 Value를 결정하는 방법이다.
• Sample Efficiency, GPU Utilization의 측면에서 장점을 가진다.

Distributed RL with decoupled architecture

Return의 기대값을 극대화하는 방향으로 Policy를 업데이트하는 강화학습에서는 현재 Policy에 따른 State, Action, Reward Transaction이 많으면 많을수록 빠르고 안정적인 학습이 가능해진다고 할 수 있다. Distributed RL은 복수의 Agent-Environment를 생성하여 Transaction을 동시에 수집하도록 하므로써 강화학습의 학습 속도를 높이는 방법이다.

논문의 저자들은 Distributed RL의 가장 대표적인 알고리즘 중 하나인 A3C(Asynchronous Advantage Actor-Critic)와 자신들이 제시하는 모델 IMPALA를 비교하는데, IMPALA가 학습 속도와 성능 면에서 보다 뛰어나며 하이퍼파라미터/모델 구조의 측면에서 보다 안정적이라고 언급한다.

Distributed RL 알고리즘으로서 IMPALA 모델은 다음 두 가지 주요한 특징을 가지고 있다.

• Communication with Trajectory
• V-Trace Target

우선 IMPALA는 Actor에서 수집한 Trajectory를 Learner에서 그대로 접근하여 학습에 활용하도록 하고 있다. 즉 Learner는 각각의 Actor 들이 수집한 Trajectory를 사용하여 batch를 구성하고, 이를 통해 Learner policy를 업데이트한다. 이때 Trajectory를 그대로 Learner에게 전달한다는 점에서 Actor가 자신이 수집한 Trajectory로부터 계산한 Gradient를 전달하는 A3C와 차이가 있다. 이때 V-Trace는 서로 다른 Actor로부터 수집된 Trajectory를 Learner가 그대로 사용할 수 있도록 해주는 방법론이라고 할 수 있다.

IMPALA Update Rule

IMPALA는 기본적으로 Actor-Critic 구조를 가지고 있어, Policy \(\pi\)와 Value function \(V^{\pi}\)를 가진다. 또한 Trajectory를 수집하는 Actor와, 수집된 Traejectory를 가지고 학습을 진행하는 Learner가 구분된다. 이때 각각의 Actor들은 자신만의 Policy \(\mu\)를 가진다.

간단히 IMPALA의 Learner Policy Update을 살펴보면 다음과 같다.

1. Actor의 Policy를 현재 Learner의 Policy에 맞춰 업데이트한다.
2. N step동안 Trajectory를 수집한다.
3. 수집한 Trajectory와 사용된 Policy를 Learner에 전달한다.
4. Learner는 Traejectory와 Policy를 바탕으로 학습한다.

이때 Actor와 Learner가 Asynchronous하게 동작하므로, 동일한 Learner에서 Policy를 복사하여 Actor가 사용하더라도 시점의 차이로 인해 Actor 간, 그리고 학습이 이뤄지는 Learner 간 Policy는 시점에 따라 서로 다를 수 있다.

Importance Sampling with Actor-Critic

이와 같이 Trajectory를 수집할 때 사용한 Policy(Actor - \(\mu\))와 학습의 대상이 되는 Policy(Learner - \(\pi\))가 서로 다른 경우를 Off-Policy 라고 한다. Actor와 Learner의 Policy가 서로 달라도 되므로 Off-Policy setting에서는 다양한 Policy가 만드는 Trajectory를 모두 학습에 사용할 수 있어 데이터 효율성이 높고, 보다 빠르게 Transaction을 수집할 수 있다는 장점을 가진다. 하지만 두 Policy 간의 차이(Policy-Lag)로 인해 Variance가 크기 때문에 학습이 불안정해지는 문제도 있다.

Importance Sampling

Importance Sampling은 이러한 두 Policy 간의 차이로 인해 발생하는 데이터의 Variance를 줄이는 방법이다. 어떤 한 분포의 기대 값을 구하기 위해 다른 분포에서 샘플링한 샘플들을 중요도(Importance)에 따라 사용하자는 것인데, 강화학습의 Off-Policy 개념에 적용해보면 Behavior Policy를 따라 샘플링한 Trajectory가 업데이트의 대상이 되는 Target Policy에서 나타날 확률에 따라 가중치를 부여하여 학습에 사용할 수 있다. Reinforcement Learning: The Introduction(Sutton)에서는 Behavior Policy \(\mu\)에서 수집한 Trajectory가 Target Policy \(\pi\)에서도 나타날 확률(Importance Sampling Ratio)을 다음과 같이 정의한다.

\[\rho_{t : T - 1} = {\Pi_{k=t}^{T-1} \pi(A_k \vert S_k) p(S_{k+1} \vert S_k, A_k) \over \Pi_{k=t}^{T-1} \mu(A_k \vert S_k) p(S_{k+1} \vert S_k, A_k)} = \Pi_{k=t}^{T-1} {\pi (A_k \vert S_k) \over \mu (A_k \vert S_k)}\]

Update Direction for Actor-Critic

Actor-Critic의 기본이 되는 Policy Graident 식은 다음과 같다.

\[\nabla_\theta J(\theta) = E_\tau [\Sigma_{t=0}^{T-1} \nabla_\theta \log \pi_\theta(a_t \vert s_t) G_t]\]

Actor-Critic은 Return \(G_t\)를 Action Value Function \(Q\)로 대체한 것이라 할 수 있다.

\[\nabla_\theta J(\theta) = E_\tau [\Sigma_{t=0}^{T-1} \nabla_\theta \log \pi_\theta(a_t \vert s_t) Q(s_t, a_t)]\]

식을 보게되면 어떤 한 State \(s_t\)에서의 Policy의 업데이트 방향은 다음과 같이 결정됨을 알 수 있다. \(q_t\)는 \(Q(s_t, a_t)\)를 근사한 값이다.

\[E_{a_t \sim \pi(\cdot \vert s_t)} [\nabla \log \pi(a_t \vert s_t) q_t \vert s_t]\]

On-Policy가 아닌 Off-Policy로서 Behavior Policy \(\mu\)와 Target Policy \(\pi\)가 서로 다르다면 Importance Sampling Ratio를 곱해주어 다음과 같이 업데이트 방향을 결정할 수 있다.

\[E_{a_t \sim \mu(\cdot \vert s_t)} [ {\pi (a_t \vert s_t) \over \mu(a_t \vert s_t)} \nabla \log \pi(a_t \vert s_t) q_t \vert s_t]\]

V-Trace Actor-Critic Algorithm

IMPALA의 Update Loss는 다음 세 가지로 구성된다.

1. Policy Gradient Loss

우선 위의 Off-Policy Policy Gradient 식과 비교해 볼 때 Action Value Function을 \(r_t + \gamma v_{t+1} - V_w(s_t)\)로 대체되었다. 이는 Action Value Function \(Q\)(s,a)에서 Baseline \(V(s)\)를 뺀 값, 즉 Advantage 이다. 이와같이 Action Value Function에 Baseline을 빼어주게 되면 Policy Gradient의 Variance가 줄어든다는 장점을 가진다. 참고로 \(V\)는 Value function, \(v\)는 V-Trace Target이다. \(\rho_t\)는 Truncated Importance Sampling Weight로 뒤에 정리해 두었다.

\[\rho_t \nabla_\theta \log \pi_\theta (a_t \vert s_t) (r_t + \gamma v_{t+1} - V_w(s_t))\]

2. Baseline Loss

Baseline \(V(s)\)를 업데이트 할 때에는 V-Trace Target \(v\)와의 거리를 줄이도록 하고 있다.

\[(v_t - V_w (s_t)) \nabla_w V_w(s_t)\]

3. Entropy Loss

마지막으로 A3C에서 도입하였듯이 충분한 Exploration이 이뤄지도록 하기 위해(혹은 premature convergence를 막기 위해) Entropy Loss를 도입하고 있다.

\[- \nabla_\theta \Sigma_a \pi_\theta (a \vert s_t) \log \pi_\theta (a \vert s_t)\]

V-Trace Target

IMPALA의 저자들이 가장 주요한 컨트리뷰션으로 언급하고 있는 V-Trace는 간단히 다른 Policy에 따라 수집된 Trajectory를 사용하는 만큼 Value를 산정할 때에 Importance Sampling을 해주자는 것으로 이해할 수 있다. 어떤 State \(s_t\)에서의 V-Trace Target \(v\)는 다음과 같이 정의된다.

\[v_{s_t} =^{def} V(s_t) + \Sigma_{k = t}^{t + n - 1} \gamma^{k - t} (\Pi_{i = t}^{k - 1} c_i) \rho_k (r_k + \gamma V(s_{k+1}) - V(s_k) )\]

여기서 \(c_i, \rho_k\)는 Importance Sampling의 Truncation level로서, 다음과 같이 정의된다.

\[\eqalign{ & c_i = \min (\bar c, {\pi (a_i, \vert s_i) \over \mu (a_i, \vert s_i)})\\ & \rho_k = \min (\bar \rho, {\pi (a_k, \vert s_k) \over \mu (a_k, \vert s_k)}) }\]

Importance Sampling을 적용하되, 일정 수준 이하로는 Weight가 떨어지지 않도록 Lower Bound(\(\bar c, \bar \rho\))를 설정하고 있다. 이를 Truncated Importance Sampling Weight라고 한다.

위의 식은 Summation 을 풀어 써보면 다음과 같다.

\[\eqalign{ v_{s_t} =^{def} V(s_t) &+ \gamma^0 \rho_t (r_t + \gamma V(s_{t+1}) - V(s_t) ) \qquad \qquad \because \Pi_{i = t}^{t - 1} c_i =^{def} 1 \\ &+ \gamma^1 c_t \rho_{t+1} (r_{t+1} + \gamma V(s_{t+2}) - V(s_{t+1}) )\\ &+ \gamma^2 c_t c_{t+1} \rho_{t+2} (r_{t+2} + \gamma V(s_{t+3}) - V(s_{t+2}) )\\ &+... }\]

\(n\)-step Target을 구할 때 \(k-1\) step까지는 \(c\)가 적용되고 마지막 \(k\)번째 Step에서는 \(\rho\)가 적용됨을 알 수 있다. 이러한 점에서 \(\rho\)는 \(k\)번째 Step의 Temporal Difference \(r_k + \gamma V(s_{k+1}) - V(s_k)\)에 적용되는 Weight이고, \(c\)는 \(k\)번째 Step에 도달하는 과정에서의 누적되는 Weight라고 할 수 있다. 논문에서는 Temporal Difference Term을 아예 다음과 같이 정의하여 이를 보다 명확하게 하고 있다.

\[\delta_k V = \rho_k (r_k + \gamma V(x_{k+1}) + V(s_k))\]

\(\rho\) and \(c\) have Different Roles

이러한 점에서 Temporal Difference 값에 곧바로 적용되는 \(\rho\)는 Value Function의 수렴 방향(Fixed Point)에 영향을 미친다. Value Function이 달라지므로 Policy의 수렴 방향도 아래와 같이 달라진다고 하는데, 증명은 논문의 Appendix에 정리되어 있다.

\[\pi_{\bar \rho} (a \vert s) =^{def} { \min (\bar \rho \mu (a \vert s), \pi(a \vert s)) \over \Sigma_{b \in A} \min (\bar \rho \mu (b \vert s), \pi(b \vert s)}\]

만약 \(\bar \rho\)의 값이 무한이라면 \(\rho\)의 값은 항상 \({\pi (a, \vert s) \over \mu (a, \vert s)}\) 가 된다. Importance Sampling Weight에 대한 Truncation이 전혀 되지 않는다는 것이고, 따라서 Value Function은 Target Policy \(\pi\)의 그것과 동일해진다. 반대로 \(\bar \rho\)의 값이 0에 가까워질수록 Behavior Policy \(\mu\)의 그것에 보다 가까워게 된다.

반면 \(c\)는 Temporal Difference에 곧장 적용되는 것이 아니므로 Value Function의 업데이트 방향에는 영향을 미치지 않는다. 다만 현재 사용하고 있는 Trajectory가 얼마나 빈번하게 발생하는지에 따라 업데이트 속도를 조절하는 역할을 한다고 볼 수 있다.

Asynchronous Update: vs. Batch A2C

V-Trace Target을 적용한 이유는 Off-Policy의 문제점 중 하나인 Policy-Lag를 해소하는 것에 있다. 이를 통해 얻을 수 있는 이점은 다음 그림에서 확인할 수 있다.

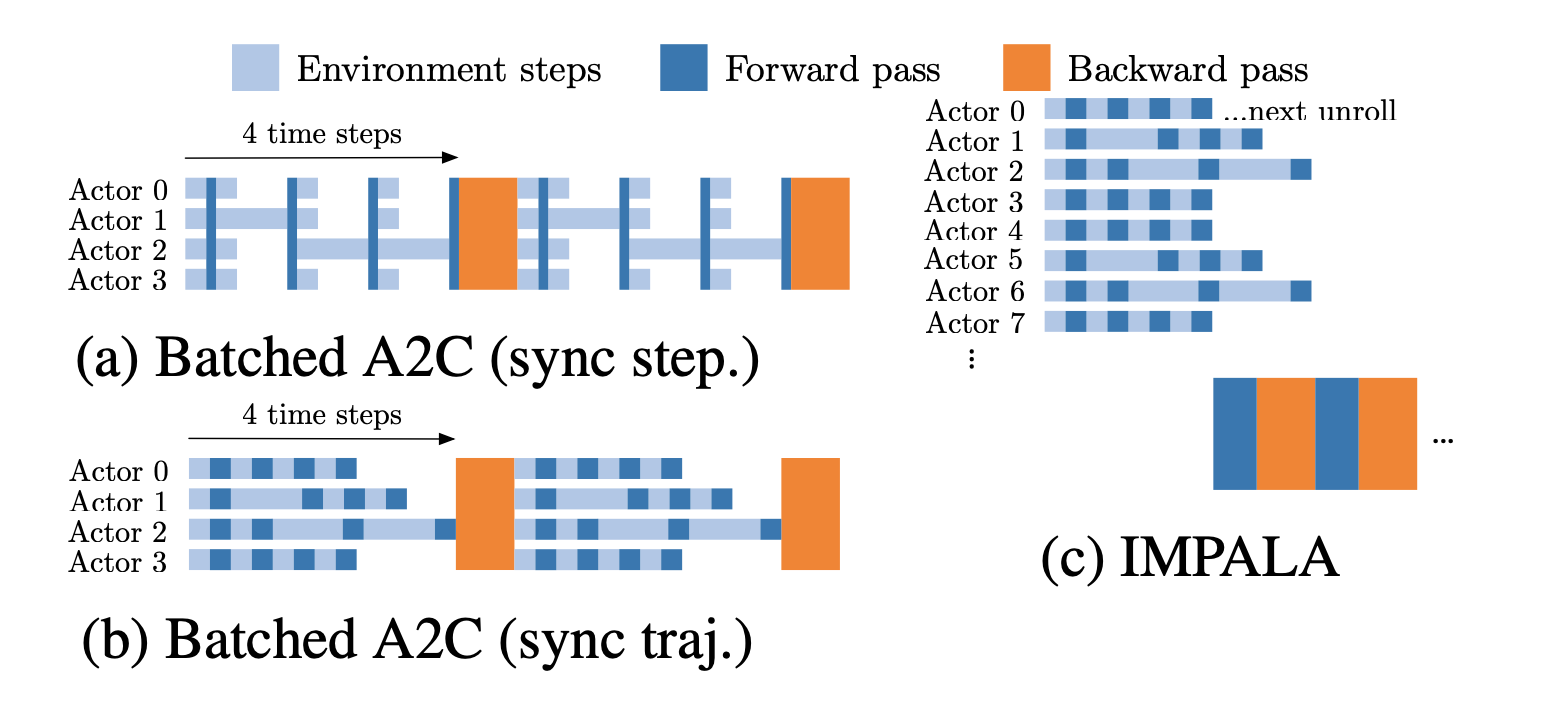
위의 이미지에서 좌측은 Batched A2C를, 우측은 IMPALA의 업데이트 방식을 나타낸다. Batched A2C의 경우 step을 맞추느냐, trajectory를 맞추느냐에 따라 다시 구분되지만, 어떠한 방식으로 하더라도 Trajectory의 길이에 따라 쉬는 Worker가 생기게 된다. 반면 IMPALA는 Worker는 Trajectory를 수집하고, 이렇게 수집된 모든 Worker의 Trajectory에 Learner가 접근하여 업데이트하기 때문에 Worker는 업데이트를 기다릴 필요가 없어진다. 이러한 점에서 GPU Utilization 등에서 이점이 있다고 논문에서는 언급하고 있다.