논문 제목 : Counterfactual Multi-Agent Policy Gradients
- Jakob N. Foerster, Gregory Farquhar 등
- 2017
- 논문 링크
Summary
- Actor-Critic 구조를 사용하는 Multi-Agent RL의 기초가 되는 논문 중 하나로, Agent의 개수만큼 Actor를 만들되 하나의 Centralised Critic만 두는 것이 특징이다.
- Credit Assignment Problem이란 각 Actor의 Gradient를 구할 때 해당 Actor의 기여(contribution)를 정확하게 반영하지 못하는 문제를 말한다.
- COMA에서는 이를 해결하기 위해 counterfactual advantage를 도입하고 있으며, 효율적인 연산을 위해 Critic에서 agent \(a\)가 수행할 수 있는 모든 Action \(u^a\)에 대한 Q value를 한 번에 계산하도록 하고 있다.
Multi-Agent RL
Multi-Agent Reinforcement Learning(MARL)은 하나의 환경에 여러 Agent가 존재하고, 각 Agent의 Action이 개별적으로 환경에 영향을 미칠 수 있는 상황을 상정한다. 이때 Agent란 Environment로부터 Observation을 수집하고, Policy에 의해 결정된 Action을 수행하는 단위를 말한다.
실제로 현실 속 많은 문제들이 Multi Agent의 특성을 가지는데 교통 혼잡이 대표적이다. 한 대의 자동차가 교통 혼잡을 피해 우회하도록 하는 알고리즘은 Single Agent로도 가능하나, 교통 혼잡 자체를 해소하고 싶다면 전체 자동차의 진로를 함께 결정해야 한다. 이러한 관점에서 Multi Agent는 여러 Agent를 동시에 훈련하여 Global Reward가 극대화되는 것을 목표로 하는 강화학습의 한 분야라고 할 수 있다.
Single Agent & Multi Agent
물론 Multi Agent의 특성을 가지는 문제들은 일반적인 Single Agent 알고리즘들로도 해결이 가능하다. Agent의 갯수에 상관없이 모든 Agent가 수집한 Observation을 하나의 Observation으로 보고, 이에 따라 Policy가 모든 Agent의 Action을 결정하도록 하기만 하면 되기 때문이다. 하지만 이 경우 Agent의 갯수가 늘어남에 따라 Action Space 또한 증가하여 차원의 저주에서 자유롭지 못하다. Multi-Agent 알고리즘들은 Single Agent 알고리즘들이 가지는 이러한 한계를 해결하는 데에 집중한다.
Centralised Training of Decentralised Policies
Multi Agent 환경에서는 Observation을 수집하고 Action을 결정하는 단위로서 Agent가 복수로 존재한다. 이때 Action을 결정하는 Policy의 위치에 따라 Centralised Policy와 Decentralised Policies 두 가지로 나누어 볼 수 있다. 단어의 의미에서 직접적으로 알 수 있듯이 Centralised Policy는 중앙에 하나의 Policy가 존재하고, 여기서 결정되는 Action을 각 Agent가 나누어 수행하는 구조를 말한다. 반면 Decentralised Polices는 각각의 Agent가 개별적인 Policy를 가지고 있고 자신만의 Observation을 바탕으로 Action을 결정하는 구조를 말한다.
Centralised Policy가 보다 단순하지만 문제 상황에 따라 Decentralized Execution을 수행해야 하는 경우에는 사용하지 못한다는 단점이 있다(실제 환경에서는 Agent 간의 Connection이 완전하지 못한 경우가 많은데 이러한 상황에서는 Centralized Policy를 사용하는 것은 다소 위험하다). 이러한 점 때문에 Decentralised Policies를 효율적으로 학습시키는 방법에 대한 연구가 활발히 이뤄지고 있으며, 논문에서는 보다 효율적인 학습이 가능하다는 장점을 가지는 Centralised Training of Decentralised Policies가 MARL 연구에 있어 주된 패러다임이라고 언급하고 있다.
Centralised Training of Decentralised Policies는 연구실과 같은 제한된 환경에서 Centralised Training에 따라 모델을 학습하고, 실제 환경에 Deploy 할 때에는 Decentralised Execution이 가능하도록 하는 방법론을 말한다. 그런데 이와 같이 Decentralised Policies를 Centralised Training에 따라 일괄적으로 학습하게 되면 Global Reward가 주어졌을 때 어떤 Policy가 얼마나 잘해서 이러한 Reward를 얻게 되었는지 정확히 알 수 없다는 문제가 있다. 이를 Multi Agent Credit Assignment 문제라고 부르며 논문에서 제시하는 모델 COMA는 이를 counterfactual baseline으로 해결하려는 접근 방법이라고 할 수 있다.
Multi Agent MDP Notation
Multi Agent에서는 Agent가 복수가 되면서 Global과 Local(individual)을 나누게 된다. 이와 관련하여 기본적인 MDP 요소들의 표기법은 다음과 같다.
| notation | desc |
|---|---|
| \(a \in A\) | Individual Agent |
| \(s \in S\) | Global State |
| \(\boldsymbol{u} \in \boldsymbol{U} = U^n\) | Joint Action |
| \(u^a \in U\) | Agent \(a\)’s Action |
| \(P(s' \lvert s, \boldsymbol{u}): S \times \boldsymbol{U} \times S \rightarrow [0, 1]\) | State Transition |
| \(r(s, \boldsymbol{u}):S \times \boldsymbol{U} \rightarrow R\) | Shared Reward Function |
이에 덧붙여 각각의 Agent가 서로 다른 것을 관찰할 수 있다는 가정(partially observable)을 위해 다음과 같은 표기법을 추가한다.
| notation | desc |
|---|---|
| \(O(s,a): S \times X \rightarrow Z\) | Observation Function |
| \(\tau^a \in T = (Z \times U)^*\) | Action-Observation History |
| \(\pi^a (u^a \lvert \tau^a): T \times U \rightarrow [0, 1]\) | Decentralisation Policies |
볼드체로 되어 있는 것은 joint를 뜻하며, 여기서는 나오지 않았지만 \(-a\)는 Agent \(a\)를 제외한 나머지 Agent에 대한 것을 의미한다.
위의 표기법에 따라 Multi-Agent Task에서 State-Value Function, Action-Value Function, Advantage function을 다음과 같이 정의할 수 있다.
\[\eqalign{ &V_\pi(s_t) = E_{s_{t+1}:\infty, \boldsymbol{u_t:\infty}}[R_t \lvert s_t]\\ &Q_\pi(s_t, \boldsymbol{u_t}) = E_{s_{t+1}:\infty, \boldsymbol{u_t:\infty}}[R_t \lvert s_t, \boldsymbol{u_t}]\\ &A_\pi(s_t, \boldsymbol{u_t}) = Q_\pi(s_t, \boldsymbol{u_t}) - V_\pi(s_t) }\]Multi Agent with Actor Critic
논문에서 제시하고 있는 COunterfactual Multi-Agent Policy Gradients(COMA)는 Actor-Critic 알고리즘 구조를 가지고 있으며, 구체적으로는 Critic은 중앙에 하나만 존재(Centralised)하고 Actor는 복수로 존재(Decentralized)하는 형태를 가진다.
Single Agent Actor Critic
Actor Crirtic은 Policy Gradient 알고리즘 중 하나로 Expected Discounted Total Reward \(J = E_\pi[R_0]\)을 극대화하기 위해 Policy Parameter \(\theta_\pi\)의 Gradient를 구하는 것에서 출발한다. 대표적인 Policy Gradient 알고리즘인 REINFORCE의 Gradient는 다음과 같이 구해진다.
\[g = E_{s_{0:\infty, u_{0:\infty}}}[\Sigma_{t=1}^{T} R_t \nabla_{\theta_\pi} \log \pi(u_t \lvert s_t)]\]이러한 REINFORCE 알고리즘의 gradient 값의 variance가 매우 커 안정적인 학습이 어렵다는 문제점을 가지고 있다는 것은 잘 알려져 있다. Actor-Critic은 이러한 전통적인 Policy Gradient의 문제를 Baseline \(b\)를 도입하여 해결하려는 방법론이라 할 수 있다. 보다 구체적으로 Action을 선택하는 Actor를 안정적으로 학습시키기 위해(Gradient의 Variance를 줄이기 위해) 위 수식에서 \(R_t\)를 \(Q(s_t, u_t) - b(s_t)\)로 바꾸게 되며, 이때 Critic은 Value Function을 추정하는 역할을 하게 된다. 참고로 \(b(s_t) = V(s_t)\)로 하는 것이 일반적이며 이 경우 \(R_t\)는 Advantage Function \(A_t({s,a})\)로 대체된다.
Independent Actor-Critic
Multi Agent에 Actor-Critic을 적용하는 가장 단순한 방법은 Actor-Critic 쌍을 필요한 Agent의 갯수만큼 만드는 것이다. 이러한 방법을 Independent Actor-Critic(IAC)라고 한다.
Counterfactual Multi-Agent Policy Gradients
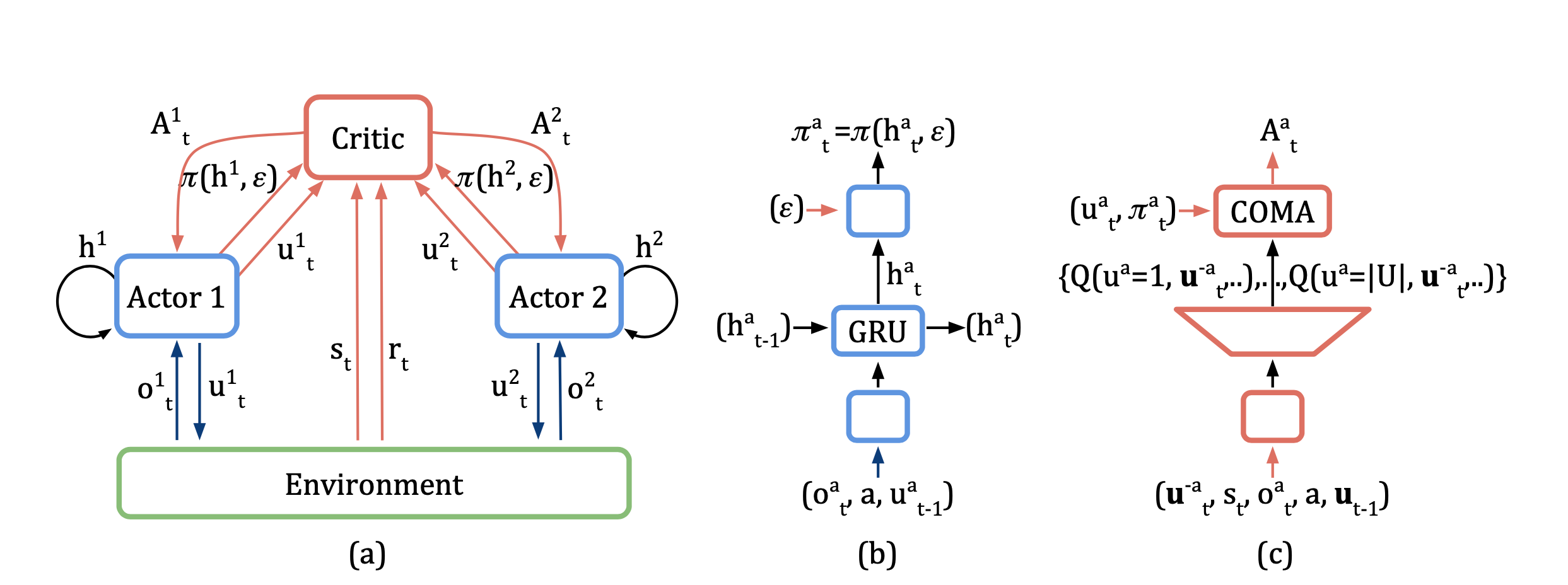
논문에서 제시하는 COMA 알고리즘은 IAC가 가지는 단점들을 극복하는 것을 목표로 한다. 이를 위해 COMA에서 도입하고 있는 방법론들은 다음과 같은 것들이 있다.
1. Centralisation of the critic
IAC에서는 필요한 Agent 수 만큼 Actor-Critic 쌍이 있으므로 actor와 critic이 \(\pi(u^a \lvert \tau^a)\), \(V(\tau^a)\) 또는 \(Q(\tau^a, u^a)\)이 모두 각 Agent의 action-observation history \(\tau^a\)에 따라 결정된다. 그러나 Actor-Critic에서 Critic은 보조적인 수단으로서 학습 시에만 사용된다는 점을 감안해 볼 때 Critic은 중앙헤 하나만 두고 모든 Actor들이 공유하도록 만드는 것도 가능하다. 이 경우 Critic은 Observation이 아닌 True Global State \(s\), 또는 Joint Action-Observation history \(\boldsymbol{\tau}\)에 따라 학습하게 된다.
Centralised Critic을 사용할 때 Actor의 Gradient는 TD-Error로 쉽게 나타내어진다.
\[g = \nabla_{\theta^\pi} \log \pi (u \lvert \tau_t^a) ( r + \gamma V(s_{t+1}) - V(s_t))\]그런데 여기서 문제가 있다면 Credit Assignment Problem, 즉 Value를 평가하는데 있어 각 Agent가 얼마나 기여했는지 평가할 수 있는 방법이 없다는 점이다. 이는 Value Function이 Global State에 따라 결정되므로 Gradient는 각 Actor들의 특성을 개별적으로 반영하지 못하는 데서 나타나는 한계라고 할 수 있다.
2. Use of a counterfactual baseline
COMA의 가장 핵심적인 부분인 Counterfactual Baseline은 이러한 문제, 즉 각각의 agent가 얼마나 잘했는지, 못했는지에 따라 Gradient를 계산하기 위한 방법으로 제시되었다. Counterfacual Baseline에서는 다음과 같이 정의된 Shaped Reward(Difference Reward)를 사용하므로서 각 Agent가 얼마나 잘하고 있는지 평가한다.
\[D^a = r(s, \boldsymbol{u}) - r(s, (\boldsymbol{u}^{-a}, c^a))\]여기서 \(\boldsymbol{u}\)는 Joint Action, 즉 Agent들이 각자 정한 Action을 하나로 묶은 것이라고 할 수 있고, \(\boldsymbol{u}^{-a}\)는 Agent \(a\)가 정한 Action은 빼고 나머지 Agent의 Action들의 집합이라고 할 수 있다. 그리고 \(c^a\)가 Agent \(a\)의 Default Action이라는 점을 생각해보면 \(r(s, \boldsymbol{u})\)는 Agent \(a\)가 고른 Action을 그대로 사용했을 때의 Reward를, \(r(s, (\boldsymbol{u}^{-a}, c^a))\)는 Agent \(a\)의 Action을 그것의 Default Action으로 바꾸었을 때의 Reward를 각각 의미한다. 이들 간의 차이로 구해지는 \(D^a\)은 그 크기가 크면 클수록 Agent \(a\)가 좋은 선택을 한 것으로 추정할 수 있으므로 Credit Assignment Problem를 해결하는 방법이 된다.
하지만 이를 곧바로 적용하는 것은 또 다른 두 가지 문제를 낳게 되는데, 첫째로는 \(r(s, (\boldsymbol{u}^{-a}, c^a))\)를 구하기 위해 추가적인 Simulator가 필요하다는 것이고, 두번째로는 Default Action을 결정하는 방법에 관한 것이다.
두 가지 문제를 한 번에 해결하기 위해 COMA에서는 Centralised Critic를 가지고 Difference Reward를 계산하는 방법을 도입했다. 구체적으로 다음과 같이 Agent \(a\)에 대한 Advantage Function를 위의 Difference Reward 형태로 변환하고, 이를 구하기 위해 Centralised Critic \(Q(s, \boldsymbol{u})\)를 적극적으로 활용하는 것이다.
\[\eqalign{ A^a(s, \boldsymbol{u}) &= Q(s, \boldsymbol{u}) - V(s) \\ &= Q(s, \boldsymbol{u}) - \Sigma_{u'^a} \pi^a ({u'}^a \lvert \tau^a) Q(s, ( \boldsymbol{u}^{-a}, {u'}^a)) \\ }\]이를 counterfactual advantage라고 부른다.
3. Use of a critic representation that allows efficient evaluation of baseline

그런데 Neural Network로 Critic을 구성하는 경우에 위 방법을 사용하면 Action의 갯수만큼 매 Agent마다 Critic을 계산해주어야 하므로 연산 횟수가 크게 늘어난다는 문제점이 발생한다. 이를 해결하기 위해 COMA에서는 다소 특수한 형태의 Critic을 사용하게 된다. 즉 입력으로 다른 agent의 Action \(\boldsymbol{u^{-a}}\) 등이 들어오면 출력으로 각 Agent \(a\)의 Action에 대한 Q value가 한 번에 나오도록 하여 counterfactual advantage를 한 번에 구할 수 있도록 한 것이다. COMA의 Critic 구조를 보여주는 왼쪽 그림에서 가운데 Neural Network를 양변 사다리꼴로 표현하고 여러 개의 Q Value를 출력하도록 하는 이유가 여기에 있다.