논문 제목 : Better Exploration with Optimistic Actor-Critic

• Kamil Ciosek, Quan Vuong 등
• 2019
• 논문 링크

Summary

• 2019 NIPS에서 발표된 model free reinforcement 의 새로운 SOTA 모델이다.
• SAC, TD3과 같은 기존 SOTA 모델은 어느 정도 학습이 이뤄지면 특정 영역에 대해 반복 탐색하게 되는 경우가 많다.
• OAC에서는 exploration policy를 별도로 두어 이러한 문제를 해결하려고 한다. 이 때 아직 탐색하지 못한 영역을 찾기 위해 q function의 upper bound 를 도입하고 이를 계산하는 방법을 제시한다. 그리고 target policy와 exploration policy 간의 차이를 조정하기 위해 KLD 제약 조건을 둔다.

Inefficiency of existing algorithms

논문은 SAC, TD3를 비롯한 지금까지의 강화학습 알고리즘들에서 사용하고 있는 탐색 방법이 비효율적이라고 주장하며, 구체적인 이유로 “pessimistic underexploration”, “directional uniformedness” 두 가지를 제시한다.

pessimistic underexploration

Actor-Critic과 같이 q value를 이용한 강화학습 알고리즘의 오랜 문제 중 하나는 q value가 overestimate 되기 쉽다는 것이다. 이러한 문제를 해결하기 위해 SAC와 TD3에서는 두 개의 critic을 만들고 두 네트워크의 출력값 중 보다 작은 것을 사용하는데, 이를 lower bound approximation 이라고 한다. 하지만 q value의 값이 여전히 부정확한 상황이라면 lower bound를 사용하는 방법 또한 여전히 위험(very harmful)하다.

논문의 figure 1a에서는 실제 q value와 lower bound q value 간의 값을 비교하며 그 위험성을 보여주고 있다. 여기서 말하는 위험성이란 q value가 높아질 가능성이 있는 영역이 있음에도 불구하고 lower bound q value가 최대화되는 지점에서 멈추고 그 주변만 탐색하게 된다는 것이다. 현재 continuous action space 문제를 해결하기 위해 강화학습 알고리즘에서 자주 사용되는 OU noise를 이용한 exploration 방법과 함께 보면 이러한 문제는 더욱 확실해진다. 즉, 어느 정도 탐색이 끝나 lower bound q value가 maximum이 되는 값에 도달하면 이를 평균으로 하는 좁은 영역만 반복적으로 탐색하게 된다는 것이다. 논문에서는 이러한 문제를 pessimistic underexploration이라고 한다.

directional uniformedness

gaussian policy를 이용하여 탐색을 하는 경우 평균을 중심으로 정방향과 역방향의 action들이 모두 둥일한 확률분포를 가지고 있다. 하지만 gradient algorithm에 따라 점진적으로 발전하는 policy network의 특성상 과거에 지나온 영역과 그렇지 않은 영역을 동일한 수준으로 exploration하는 것은 비효율적이다. 논문에서는 이를 두고 “Exploration in both directions is wasteful”이라고 언급한다.

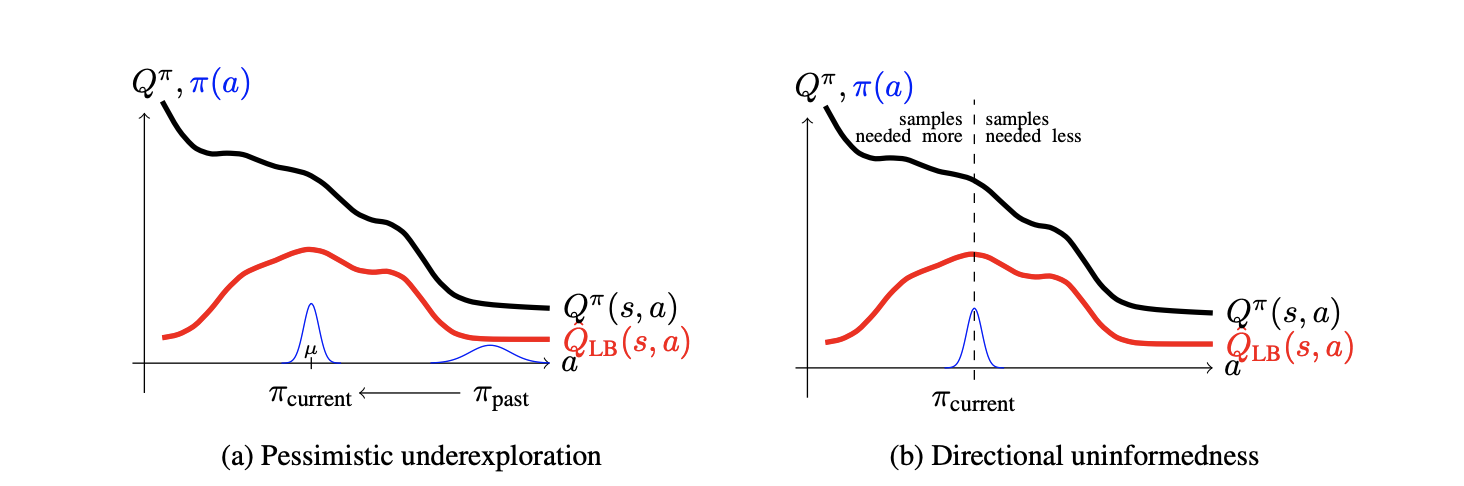
exploration과 관련된 위의 두 가지 문제는 논문에 제시되어 있는 위의 그림을 참고하면 보다 쉽게 이해할 수 있다. 기본적으로 위의 그림은 어떤 고정된 state \(s\)에서 action \(a\)에 따른 Q function 값의 변화를 보여주고 있다.

우선 왼쪽 그림을 보면, 과거의 policy \(\pi_{past}\)에서 학습을 통해 \(\pi_{current}\)로 나아가는 모습을 표현하고 있다. 기존의 알고리즘은 모두 Lower bound를 기준으로 했으므로, lower bound q function \(Q_{LB}(s,a)\)가 극대화되는 지점을 평균으로 하는 위치에 머무르게 된다. 그런데 학습 경로 상에 \(\pi_{past}\)부터 \(\pi_{current}\)에 이르는 영역 사이의 action에 대해서는 충분히 학습했지만 그보다 왼쪽에 위치한 action들은 선택해 본 경험이 없다. 이러한 문제를 논문에서는 pessimistic underexploration 문제라고 하는 것이다.

오른쪽 그림은 Directional uniformedness를 표현하고 있는데, 가우시안 분포의 특성상 거쳐온 쪽(그림상에서 오른쪽)과 그렇지 않은 쪽(왼쪽)을 동일한 확률로 action을 선택하게 되는데, 앞서 설명한 이유 때문에 이것 또한 비효율적이라는 것이다.

그리고 기존의 알고리즘에 따르면 학습이 어느 정도 이뤄져 lower bound 근처에 도달하게 되면 큰 변화없이 비슷한 지역을 반복적으로 학습한다는 문제도 있어 낭비적이라고 한다.

Exploration policy

위에서 제시한 기존 강화학습 알고리즘들의 문제들은 exploration과 관련된 것으로, 이를 해결하기 위해 OAC에서는 exploration policy를 별도로 두고 있다.

exploration policy는 upper bound q value와 KL Divergence를 이용한다. 간단히 설명하자면 upper bound q value를 이용해 지금까지 탐색하지 못한 영역에 접근할 수 있도록 하되, KL divergence로 제약을 두어 exploration policy에 따른 탐색 영역이 target policy의 결과와 크게 달라지는 것을 방지한다.

exploration policy는 target policy와 마찬가지로 가우시안 분포이다. 따라서 평균과 표준편차만 구하면 된다. 수식으로 exploration policy의 평균 \(\mu_e\)와 표준편차 \(\sigma_E\)는 다음과 같이 구해진다.

\[\mu_e, \Sigma_E = \text{argmax}_{\mu, \Sigma: KL(N(\mu,\Sigma), N(\mu_T, \Sigma_T)) \le \delta} \ E_{a-N(\mu,\Sigma)}[\bar Q_{UB}](s,a)\]

Upper bound의 기대값을 최대로 하되, target policy와 KLD를 통해 일정 수준 이상으로 멀어지지 않도록 제약을 두고 있음을 알 수 있다.

upper bound \(\bar Q_{UB}\)

논문에서는 uppder confident bound에 근사하기 위해 세 단계를 거친다고 한다. 첫 번째는 true Q의 평균과 표준편차를 구하는 것이고, 두 번째는 Q의 평균과 표준편차를 이용해 expected upper bound를 찾는 것이다. 세 번째는 다시 이 expected value를 linear approximation하여 보다 다루기 쉬운 알고리즘을 얻는 과정이다.

1. ture Q value

첫 번째는 true Q의 평균과 표준편차를 구하는 문제이다. 두 가지를 정확하게 구하는 것은 쉽지 않는데, 그 이유를 epistemic uncertainty, 즉 정보가 부족하여 불확실한 상황이라고 표현하고 이러한 문제를 해결하기 위해 가우시안 분포로 모델링하고 있다.

true Q의 평균과 표준편차는 부트스트랩을 이용해 다음과 같이 구했다고 한다.

\[\mu_Q(s,a) = {1 \over 2}(\hat Q_{LB}^1(s,a) + \hat Q_{LB}^2(s,a))\] \[\sigma_Q(s,a) = \root \of {\Sigma_{i \in \{ 1,2 \} } {1 \over 2} ( Q_{LB}^i(s,a) - \mu_Q(s,a) )^2 } \\ = {1 \over 2} | \hat Q_{LB}^1(s,a) - \hat Q_{LB}^2(s,a) |\]

2. expected upper bound

위에서 구한 true Q value를 이용해 expected upper bound는 다음과 같은 수식으로 표현될 수 있다고 한다.

\[\hat Q_{UB}(s,a) = \mu_Q(s,a) + \beta_{UB}\sigma_Q(s,a)\]

3. linear approximation of upper bound

위의 식을 보다 쉽게 다루기 위해 다음과 같은 linear function으로 변환해준다.

\[\bar Q_{UB}(s,a) = a^T[\nabla_a \hat Q_{UB}(s,a)]_{a=\mu_T} + const\]

테일러 정리에 따르면 위 식은 어떤 고정된 state \(s\)에서 현재 policy의 평균 \(\mu_T\)가까이의 작은 영역에서 선형적으로 \(\hat Q_{UB}(s,a)\)에 맞춘 것이 된다. 위의 식에서 Gradient가 되는 \([\nabla_a \hat Q_{UB}(s,a)]_{a=\mu_T}\)는 lower bound의 gradient와도 계산적으로 유사하기 때문에 쉽게 얻어질 수 있다는 장점도 있다.

KL Divergence constraint

q function의 upper bound만 극대화하는 방향으로 탐색이 이뤄지면 실제 target policy와 exploration policy 간의 차이가 매우 커질 수도 있다. 이 경우 update의 안정성에 문제가 생길 수 있어, target policy와 exploration policy 간의 차이를 일정 수준 이내로 조정할 필요가 있다. 이러한 문제를 해결하기 위해 OAC에서는 두 분포 간의 KLD를 일정 수준 이내로 제약 조건을 도입하고 있다.

return to exploration policy

위에서 exploration policy를 아래와 같이 제시했었다.

\[\mu_e, \Sigma_E = \text{argmax}_{\mu, \Sigma: KL(N(\mu,\Sigma), N(\mu_T, \Sigma_T)) \le \delta} \ E_{a-N(\mu,\Sigma)}[\bar Q_{UB}](s,a)\]

결과적으로 보면 위에서 구한 upper bound \(\bar Q_{UB}(s,a)\)를 극대화하는 동시에 KLD로 제약을 두는 것이 된다. 여기서 첫 번째, 즉 upper bound를 극대화하는 것은 정보가 많을 것으로 추측되는 action을 선택할 가능성을 높이는 것으로 해석(principle of optimism in the face of uncertainty)될 수 있다.

두 번째 target policy \(\pi_T\) KLD를 와의 차이를 일정 수준 이하로 제한하는 것은 안정적인 업데이트를 위한 것이라고 한다. 이는 두 가지로 다시 해석될 수 있는데, 실제 action과 너무 다른 action을 취하여 해선 안되는 행동들(catastrophic)을 선택하는 것을 방지할 수 있다는 것이 한 가지 이유이고, \(\bar Q_{UB}\) 역시도 근사값이므로 정확도에 있어 문제가 생길 수 있는 만큼 그나마 정확할 것으로 예상되는 target policy 근처의 action만 선택하도록 하는 것이 다른 이유가 된다.

exploration policy algorithm

두 개의 가우시안 분포와 선형구조를 가진 \(\bar Q_UB\)로 이뤄져 있으므로 최종적으로 exploration policy 알고리즘은 다음과 같이 closed form 으로 표현할 수 있다.

\[\mu_E = \mu_T + { \root \of {2 \sigma} \over {|| [\nabla_a \hat Q_{UB}(s,a)]_{a=\mu_T} ||_{\Sigma}}} \Sigma_T[\nabla_a \hat Q_{UB}(s,a)]_{a=\mu_T}\] \[\text{and} \ \Sigma_E = \Sigma_T\]

이때 exploration policy의 공분산은 target policy의 그것과 같다는 것을 증명했다고 한다.

effect of exploration policy

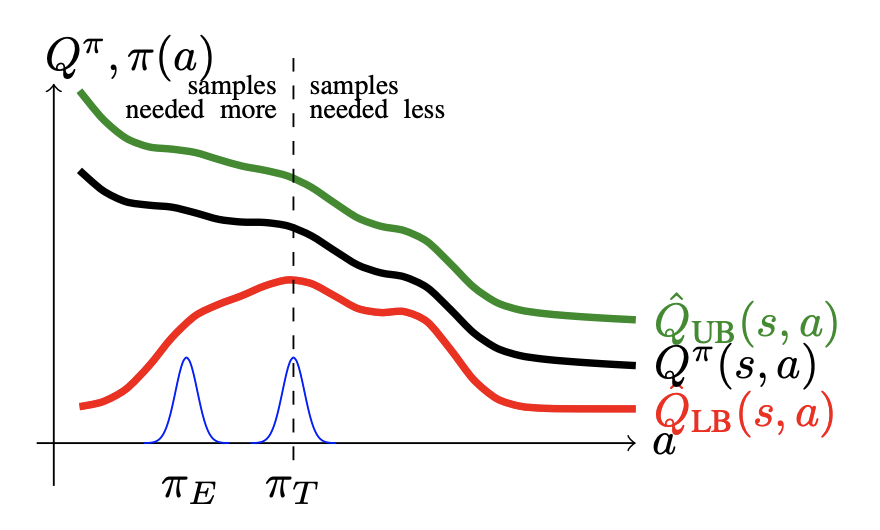
기존의 방법들이 \(\pi_T\)에서 더 이상 내려가지 못하고 머물렀다면, exploration policy \(\pi_E\)를 도입하여 OAC는 기존에 탐색하지 못한 영역까지 탐색할 수 있게 되었다고 한다. 그리고 반복적으로 어떤 영역을 탐색하는 것이 아니므로 효율적(optimistic)하다고 말한다.