논문 제목 : World Models
- DavidHa, JurgenSchmidhuber
- 2018
- 논문 링크
Summary
- 강화학습의 많은 문제들은 현재 State에 대한 정보 뿐만 아니라 미래에 대한 예측 정보를 함께 사용할 때 보다 높은 성능을 보일 수 있다.
- World Model의 구성요소인 M Model에서는 MDN-RNN 구조를 통해 예측 정보를 만들어내고, 이를 바탕으로 C Model은 보다 나은 Action을 결정한다.
- V Model, M Model과 비교해 볼 때 Decision Making을 하는 C Model은 상대적으로 크기가 매우 작으며 CMA-ES라는 Evolutionary Strategy를 통해 업데이트한다.
Introduction
144Km/h의 야구공이 투수의 손을 떠나 포수의 미트 속으로 들어가는 데에 걸리는 시간은 약 0.4초 정도이다. 정확한 의사결정을 내리기에는 너무 짧아 보이지만 타석에 들어선 타자는 스윙을 할 것인지, 말 것인지, 한다면 어떻게 할 것인지 결정하고 실행에 옮겨야 한다. 이것이 가능한 이유에 대해 심리학자들은 타자들이 무의식 중에 예측을 하기 때문이라고 설명한다. 야구공이 투수의 손을 빠져나와 자신에게로 날아오기 시작할 때의 시각 정보를 처리하며 타자들의 뇌는 반사적으로 야구 공의 예상 궤적을 예측하고 이에 따라 스윙의 여부를 결정한다는 것이다.
이와 같이 인간의 뇌는 움직이고 있는 물체가 앞으로 어떻게 운동할 것이고, 그 결과 자신이 얻을 수 있는 감각은 어떠할 것인지 예측하고 그에 맞춰 행동하는 능력을 가지고 있다고 한다. 또한 이 과정에서 무수히 많은 데이터를 추상화하여 처리하고 끊임없이 학습한다고 한다. 본 논문에서 제시하고 있는 World Model은 이러한 인간의 인지적 작용을 모사하려는 시도라고 할 수 있다.
Model Architecture
이와 같은 뇌의 작용을 모사하기 위해 World Model에서는 전체 Agent를 입력 state로 부터 특징을 추출하고 그에 맞춰 다음 state를 예측하는 부분과 이러한 예측에 따라 최적의 행동을 결정하는 부분으로 나누고 있다. 이때 특징을 추출하고 예측하는 부분을 World Model이라고 하고, 행동을 결정하는 부분을 Controller Model이라고 한다.
World Model 부분의 성능이 탁월하여 환경으로부터 받은 State에서 의사결정에 필요한 정보만을 추출하고 미래에 어떠한 정보가 들어올지 정확히 혜측할 수 있다면 Policy는 보다 풍부한 정보를 바탕으로 Action을 결정할 것으로 기대할 수 있다. 이와 관련하여 논문에서는 다음과 같이 표헌하고 있다.
- “By training the agent through the lens of its world model, we show that it can learn a highly compact policy to perform its task”
Credit Assignment Problem 등의 이유로 다른 분야의 Deep Learning 알고리즘과 비교해 Model-Free 강화학습 알고리즘들의 Policy Network 크기는 매우 작은 편이다. 이러한 제약조건이 존재하는 상황에서 World Model은 작은 Policy Network 크기를 유지하면서도 환경으로부터 많은 정보들을 처리할 수 있어 다른 알고리즘들에 비해 탁월하다고 한다.
세부적으로 보면 Model은 아래 그림과 같이 세 가지 Model, V Model, M model, C Model로 구성되어 있다.
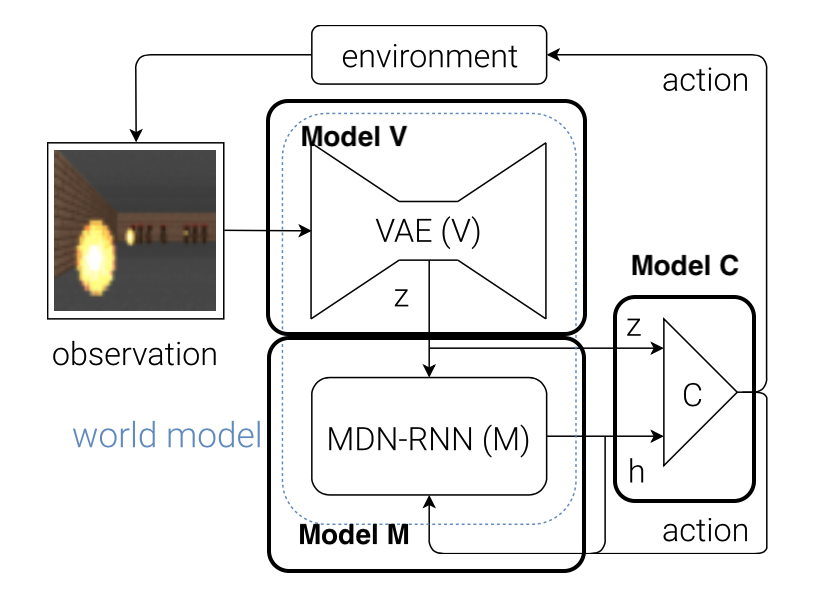
V Model
V Model은 State 정보를 가장 먼저 받아들이는 부분으로 State에서 중요한 정보를 추출하는 역할을 수행한다. 즉 Observation을 Small Representation을 변화시키는 것을 목표로 한다. 이때 사용하는 것이 VAE(Variational Auto Encoder)로, VAE의 Latent \(z\)를 State의 Small Representation으로 사용한다.
M Model
V Model이 각 시점 \(t\)에 들어온 State 정보 \(s_t\)에서 특징을 추출하는 역할을 한다면 이후에 오는 M Model은 미래 State를 예측하는 역할을 한다. 시간 순으로 들어오는 State 정보들을 입력으로 받기 때문에 RNN으로 처리하고 있다. 또한 많은 환경들이 Stochastic 하므로 이에 대한 대처 능력을 높이기 위해 Mixture Density Network(MDN)를 사용한다.
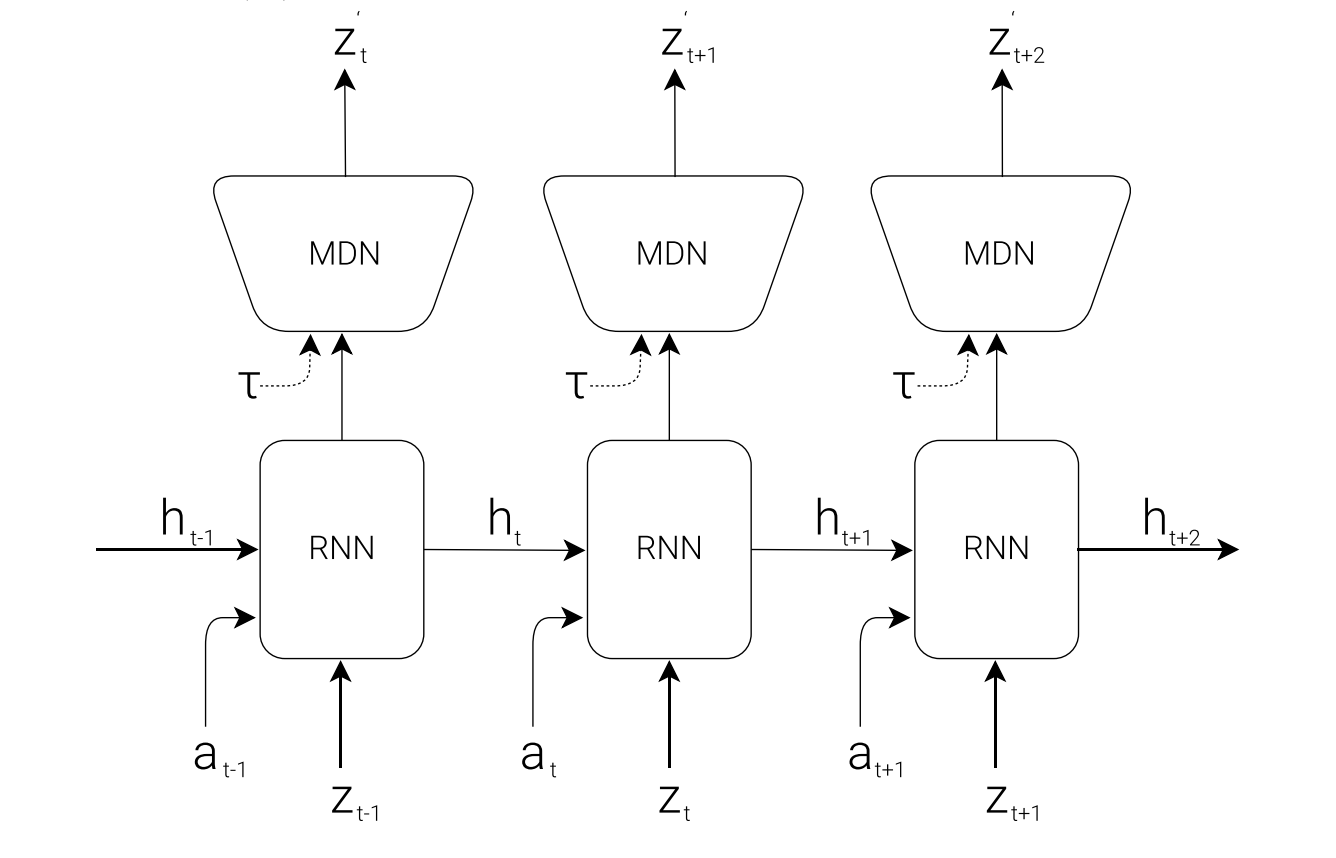
MDN은 논문의 각주에 나와있듯 Bishop이 논문 Mixture Density Networks에서 제시하는 방법으로, 하나의 입력 \(x\)에 대해 다양한 결과가 존재할 수 있음을 가정하고 그에 맞춰 여러 개의 확률 분포를 가정하는 확률 모델이라고 할 수 있다. 정규 분포를 가정한 MDN의 수식은 다음과 같다.
\[p(y \lvert x) = \Sigma_{i=1}^n (c=i \lvert x) N(y; \mu_i, \sigma_i)\]MDN을 적용하는 이유는 투수가 변화구를 던지는 상황을 생각해보면 쉽게 이해가 된다. 투수가 포심을 던질지 체인지업을 던질지 모르는 상황에서 (그립을 보면 알 수 있겠지만 현실적으로는 불가능하니까) 공이 손을 빠져나오는 장면 만으로는 궤적을 알기 어렵기 때문에 타자는 다양한 구종을 생각해야 한다. 이와 같이 Stochastic한 상황에서는 다양한 궤적을 고려하는 것이 보다 효과적일 것이다. 이러한 점에서 MDN은 포심일 때의 정규 분포, 체인지업일 때의 정규 분포를 모두 고려하도록 하는 장치로 이해할 수 있다.
M Model는 다음과 같은 수식으로 정리할 수 있다.
\[P(z_{t+1} \lvert a_t,z_t,h_t)\]위의 그림에서도 확인할 수 있겠지만 현재 시점의 state에 대한 represenation인 \(z_t\)와 함께 action \(a_t\), RNN의 이전 시점 Hidden state인 \(h_t\)를 입력으로 받아 \(h_{t+1}\)를 출력하여 MDN으로 전달하고, 이를 바탕으로 MDN은 \(z_{t+1}\)을 뽑아내도록 되어 있다. 참고로 그림 상의 \(\tau\)는 MDN에서 샘플링을 할 때 불확실성의 정도를 조절하는 Temperature parameter라고 한다.
C Model
마지막 C Model은 Contorller, 즉 Action을 결정하는 Policy라고 할 수 있다. 일반적인 강화학습의 Policy라면 현재 시점에서 얻은 State 정보, 즉 \(s_t\)만을 사용하여 Action \(a_t\)를 결정하게 될 테지만(\(\pi(a_t \lvert s_t)\)) World Model의 Policy는 현재 State를 반영하는 \(z_t\) 뿐만 아니라 이전 시점의 State와 Action 정보를 사용하여 얻은 예측 \(h_t\) 또한 함께 사용하여 현재의 Action \(a_t\)를 결정하게 된다. 아래 수식과 같이 C Model은 하나의 레이어로 구성되는 Fully Connected Network이며, \(z_t\)와 \(h_t\)를 Concat하여 입력으로 전달한다.
\[a_t = W_c [z_t, h_t] + b_c\]논문에서는 C Model을 최대한 작게 만드는 방향으로 실험을 진행했다고 한다. 그리고 C Model의 학습과 관련하여 특이한 점이 있다면 C Model을 업데이트 할 때 Covariance-Matrix Adaptation Evolution Strategy(CMA-ES)라 불리는 진화 전략(Evolution Strategy) 알고리즘을 사용한다는 점이다. 이는 V Model과 M Model과 비교해 파라미터의 갯수가 상대적으로 작다는 점을 고려한 것이라고 한다.
Full Process
세 개로 나눠져 있고 이전 시점이 현재 시점에 계속해서 영향을 주기 때문에 전체적인 프로세스가 복잡한 편이므로 다음과 같이 그림으로 표현하면 보다 쉽게 이해할 수 있다.
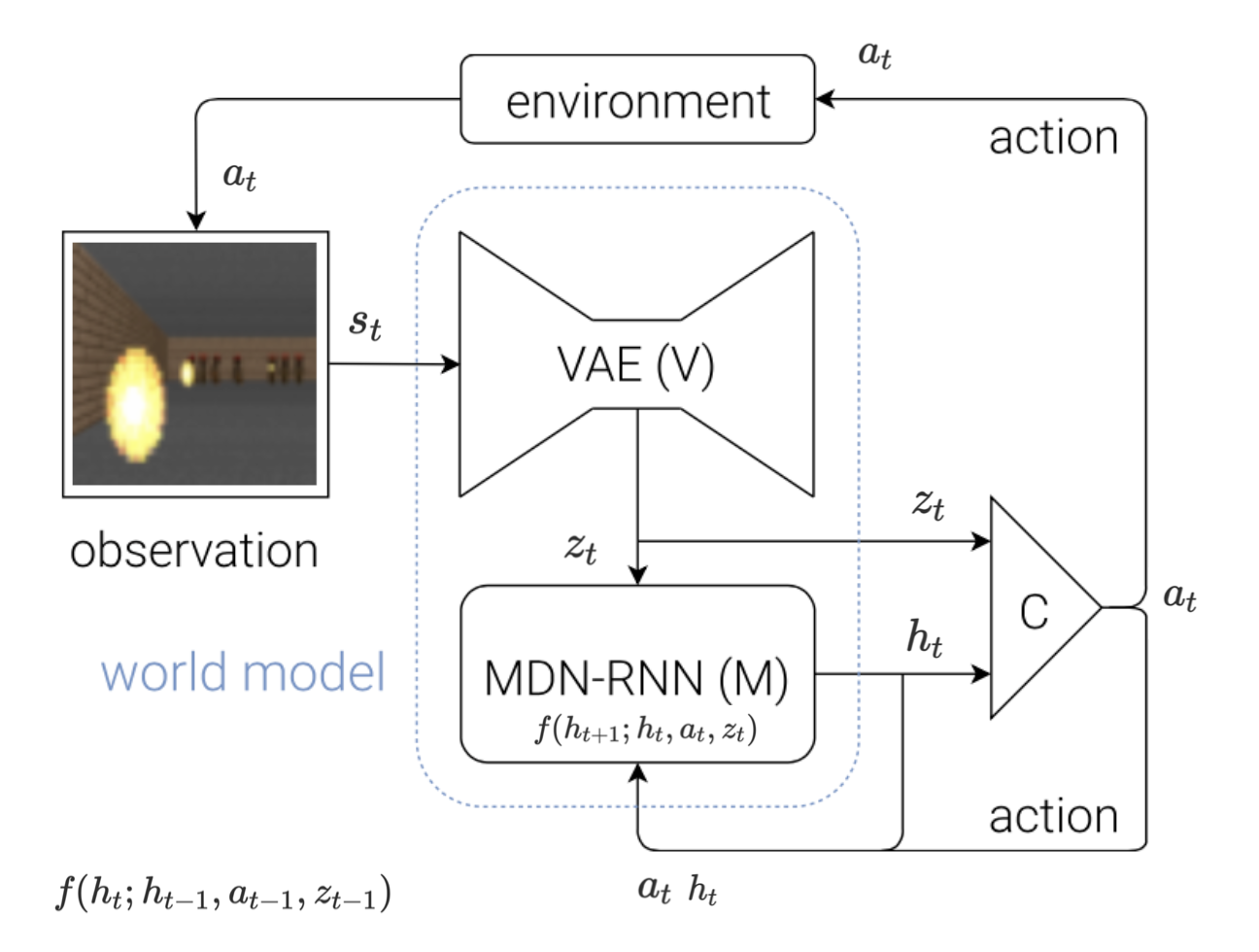
- 환경으로부터 State \(s_t\)를 입력으로 받는다.
- V Model에 \(s_t\)를 입력으로 전달하고, 출력으로 \(z_t\)를 받는다.
- \(z_t\)를 C Model에 전달한다.
- C Model은 \(z_t\)와 이전 시점에 만들어진 \(h_t\)를 사용하여 Action \(a_t\)를 결정한다.
- 환경은 \(a_t\)를 받아 \(s_{t+1}\)로 넘어간다.
- M Model은 V Model의 \(z_t\), C Model의 \(a_t\), 그리고 자기 자신의 \(h_t\)를 통해 다음 time step에 사용할 \(h_{t+1}\)을 만들어둔다.
How to Train: Car Racing Experiment
논문에서 실험 환경으로 사용된 것은 CarRacing-v0으로 Action은 방향(Left, Right), Accelerator, Brake 세 가지로 구성되고, Reward는 정해진 시간 동한 통과한 타일의 갯수로 측정되는 환경이다. 이러한 환경에서 다음과 같은 순서에 따라 World Model에 대한 학습을 진행했다고 한다.
- Random Policy를 사용하여 10,000번의 Rollout 동안 얻은 데이터를 수집한다.
- 1에서 수집한 데이터를 바탕으로 \(z \in R^{32}\)을 가지는 Model V를 학습시킨다.
- \(P(z_{t+1} \lvert a_t, z_t, h_t)\)에 따라 Model M을 학습시킨다.
- Model C를 \(a_t = W_c [z_t, h_t] + b_c\)로 정의한다.
- CMA-ES 방법에 따라 \(W_c\)와 \(b_c\)를 기대 누적 Reward가 극대화되도록 학습시킨다.
여기서 Rollout이란 Episode와 유사한 개념으로 다음과 같이 정의된다.

그리고 3번에서 M Model을 학습시킬 때에는 1,2번에서 수집한 데이터들을 사용한다. 즉 Random Action들과 당시의 State에 대한 Latent vector를 가지고 학습을 진행하게 된다. 그리고 식에서도 확인할 수 있지만 Model V와 Model M은 Reward에 대해서는 어떠한 정보도 얻지 못하고, 오로지 C Model 만이 Reward에 대해 학습한다.
Experiment Result
실험 결과와 관련하여 재미있는 점 중 하나는 M Model을 사용하지 않은 경우, 즉 예측에 관한 정보를 Model C가 얻지 못한 경우에 대해서도 실험을 진행했다는 점이다. 그 결과는 아래와 같다.

V Model만을 사용한 경우에도 성능이 A3C와 유사하게 나오는 것을 확인할 수 있다. 다만 Variance가 상당히 큰 것을 알 수 있는데, 이는 VAE에서 \(z_t\)를 추출하는 과정에서 정보 손실이 발생했기 때문으로 추측된다. 참고로 V Model with Hidden Layer는 C Model에 하나의 Hidden layer를 더 추가한 경우라고 한다.
Dream World
논문에는 한 가지 재미있는 표현이 등장하는데 실제 State로 부터 정보를 받아오지 않고 M Model의 예측값 \(z_{t+1}\)을 다음 State로 간주하는 방식으로도 실험하는 것이 가능한데, 이를 Dream이라고 표현한다. M Model의 학습이 잘 이뤄져 있다면 예측값 \(z_{t+1}\)을 VAE의 Decoder에 넣었을 때 실제 환경과 유사한 결과를 얻을 수 있다고 한다. 그리고 이때 Temperature Parameter \(\tau\)를 통해 M Model의 예측이 가지는 불확실성의 정도를 조절하는 것이 가능하다. 이와 같은 특성이 Model Based Algorithm으로서 World Model의 특징을 가장 잘 보여주는 것이라 할 수 있다.
Iterative Training Procedure
위에서 제시한 학습 방법은 V Model과 M Model을 Random Policy로 경험한 환경에 대해서만 학습이 이뤄지도록 하고 있다. 이러한 방법은 환경이 비교적 단순하고 일관된 경우에는 가능하나, 현실을 비롯하여 보다 복잡하고 확률적인 환경에서는 정보를 제대로 추출해내지 못할 가능성이 높다. 이를 극복하기 위해서는 C Model을 업데이트한 후에 얻은 정보를 사용하여 지속적으로 모델을 개선하는 것이 필요하다. 그 과정에서 업데이트 과정에 약간의 차이가 생기게 되는데 그 내용은 다음과 같다.
- M Model, C Model을 Random Parameter로 초기화한다.
- \(N\)번의 Rollout을 수행하고 그 과정에서 사용한 Action \(a_t\)와 Observation \(x_t\)를 모두 수집한다.
- \(P(x_{t+1}, r_{t+1}, a_{t+1}, d_{t+1} \lvert x_t, a_t, h_t)\)에 따라 M Model에 대해 학습을 진행한다. 그리고 M Model에 따라 C Model에 대해서도 기대 누적 rewrad를 극대화하는 방향으로 학습을 진행한다.
- 2번으로 돌아가서 다시 시작한다.
3번 식에서 나오듯이 Iterative Training Procedure에서는 M Model을 학습할 때
\[P(z_{t+1} \lvert a_t, z_t, h_t)\]가 아니라
\[P(x_{t+1}, r_{t+1}, a_{t+1}, d_{t+1} \lvert x_t, a_t, h_t)\]에 따라, 즉 입력 \(x_t\)뿐만 아니라 Action, Reward, Done과 같은 정보들도 예측하도록 하고 있다. 이와 관련하여 논문에서는 Walking Robot과 같이 복잡하고 정밀한 제어가 필요한 Task를 목적으로 한다면 C Model이 어떻게 행동할지 또한 M Model이 예측하도록 하여 C Model이 보다 복잡한 환경에 잘 적응할 수 있도록 도울 수 있다고 한다.
Loss of M Model
논문에서는 M Model의 Loss를 기준으로 Agent가 많이 경험하지 못한 상황을 판단할 수 있다고 한다. 즉 M Model이 예측한 \(z_{t+1}\)이 실제 \(z_{t+1}\)과 많이 다르다면 지금까지 많이 본 적이 없어서 예측을 잘 못한다는 것으로 보고, 이에 관한 데이터를 수집하고 다음 학습에 사용하겠다는 것이다.