논문 제목 : A Distributional Perspective on Reinforcement Learning

• Bellemare 등
• 2017
• 논문 링크

Summary

• 실제 환경에서는 동일한 state에서 동일한 action을 한다고 하더라도 reward 또는 기대 return 이 다른 경우가 많다. 이러한 상황에 보다 잘 대처하기 위해 distributional RL을 제안한다.
• distributional RL에서는 Q value를 scalar 값으로 구하는 것이 아니라 분포의 형태로 먼저 구한 뒤 그것의 기대값(평균)을 Q value로 사용한다.
• update 식에서 분포 간의 거리를 이용하여 Loss를 계산하게 되는데, wasserstein distance가 더욱 적합한다는 것을 보이고 있지만 , 적용하지 못하고 KLD를 사용하고 있다.

Intro to Distributional Perspective RL

기본적으로 강화학습에서 \(Q(s,a)\)는 expected bellman equation이라는 표현처럼 그 자체로 기대값의 개념을 포함하고 있지만 단일의 scalar 값으로 구해진다. 반면 distributional RL은 기대값을 곧바로 특정한 값으로 구하여 결정하지 않는다. 대신 \(Q(s,a)\)를 추정하기 위한 value distribution을 먼저 구하고 이 distribution의 기대값을 \(Q(s,a)\)로 사용한다. 이를 위해 논문에서는 distributional bellman equation을 정의하고 있다.

논문에서는 value distribution을 우선 설정하고 이에 대한 기대값을 얻는 방식으로 Q value를 구하는 것이 알고리즘적 관점에서 더 좋다고 주장하고 있다. distributional RL은 학습 과정에서 multimodality를 보존하기 때문에 보다 안정적인 학습이 가능해지고, 하나의 값이 아닌 분포로 표현하기 때문에 policy가 안정적이지 않아 생기는 문제를 완화시켜준다는 점 등을 그 이유로 제시하고 있다.

Approximate Distributional Learning

논문에서는 아래의 그림과 같이 C51 알고리즘을 다음 네 단계로 설명하고 있다.

Value distribution for state-action pair

위의 그림은 action의 value distribution을 표현한 것으로 이산확률분포의 형태를 띄고 있는 것을 확인할 수 있다. 각각의 분포는 어떤 action의 value distribution인데, 이를 위해서 세 가지 하이퍼파라미터를 설정해줘야 한다. 우선 \(V_{MIN}\)과 \(V_{MAX}\)는 표현하고자 하는 값의 범위를 설정한다. \(N \in \rm I\!N\)은 category의 개수를 의미하는데, 알고리즘에서는 이를 support라고 표현한다. support 그 자체의 값은 전체 return을 의미하고, 각 support의 값은 해당 support의 값이 주어질 확률을 뜻한다. 이때 확률값은 소프트맥스를 통해 총합이 1이 되도록 맞춘다.

구체적으로 support의 값과 확률은 다음과 같이 \(z_i,\ p_i(s,a)\)로 표현된다.

\[Z_\theta (s, a) = z_i \quad \quad w.p. \ p_i(s,a) = { {e^{\theta_i (s,a)}} \over {\Sigma_j e^{\theta_j (s,a)}}}\]

그리고 support 값과 확률을 곱해 모두 더하면 해당 action의 기대값, 즉 \(Q\) value가 된다.

\[Q(s,a) = \Sigma_i z_i p_i (s,a)\]

Updating Policy

distributional RL에서도 기본적인 강화학습 알고리즘과 마찬가지로 target value와 current value 간의 차이를 이용하여 학습하게 된다. policy를 업데이트하기 전에 현재 policy가 얼마나 좋은지 평가하는 과정이 필요한데, 이를 위해 논문에서는 다음과 같이 알고리즘적인 논의를 진행한다.

1. target distribution

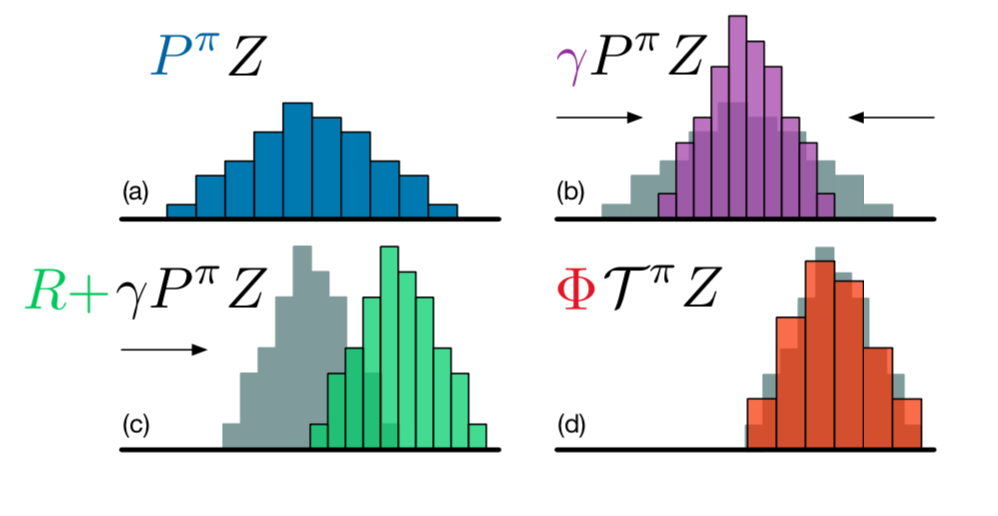
위의 그림에서 (a)에 해당하는 파란색 그림은 어떤 state-action pair \((s,a)\)의 분포에 해당하는 네트워크의 출력값을 그대로 받아온 것으로, 이를 \(P^\pi Z\)라고 한다. 논문에서는 아래와 같은 notation을 이용하여 distributional RL에서 현재의 분포와 다음의 분포를 구하는 과정을 보여주고 있다.

\[\begin{multline} \shoveleft V^\pi \text{ : value function given policy} \ \pi \\ \shoveleft Z^\pi \text{ : value distribution given policy} \ \pi \\ \shoveleft \tau^\pi \text{ : policy evaluation operator} \\ \shoveleft R \in Z \text{ : reward function as a random vector}\\ \shoveleft P^\pi \ : \ Z \rightarrow Z \text{ : transition operator}\\ \end{multline}\]

여기서 bellman operator는 bellman equation을 vector 간의 연산으로 표현한 것으로 자세한 설명은 글 마지막 additional study에 추가해 두었다.

현재 state-action pair와 다음 state-action pair 간에는 아래와 같은 등식이 성립한다고 정의할 수 있다. 즉, policy \(\pi\)를 따를 때 다음 step에 어떤 distribution에서 다른 distribution으로 바뀌는 것을 \(P^\pi\) operator를 이용해 표현하고 있는 것이다.

\[P^\pi Z(s,a) := Z(S', A') \\ S' - P(\cdot | s, a), \ A' - \pi(\cdot | S')\]

이에 따라 distributional bellman operator \(\tau^\pi \ : \ Z \rightarrow Z\) 또한 아래와 같이 정의할 수 있다.

\[\tau^\pi Z(s, a) := R(s,a) + \gamma P^\pi Z(s,a)\]

즉 위의 첫 번째 그림(파란색 플롯)은 policy \(\pi\)를 따를 때 next state의 value distribution을 의미한다. 두 번째는 그것에 감가율 \(\gamma\)가 곱해진 것으로 항상 \(0 \leqq \gamma \leqq 1\)이 성립하기 때문에 감가율을 곱한 (b)에서는 그 폭이 줄어들게 된다. 그리고 이어 reward value \(R\)을 더해주게 되는데, 그 결과 분포는 수평이동하게 된다(c).

2. projection

하지만 이 경우 \(P^\pi Z\)와 \(\tau^\pi Z\)의 차이를 곧바로 확인하는 것이 어려운데, 왜냐하면 감가율을 곱하고 reward를 더하는 과정에서 support의 크기가 달라지기 때문이다. 따라서 새롭게 만들어진 분포를 projection하여 기존의 support와 맞춰줄 필요가 있다. 논문에서는 다음과 같은 공식을 통해 projection을 진행했다고 한다.

\[(\Phi \hat \tau Z_\theta(s,a))_i = \sum_{j=0}^{N-1} [ 1 - (\ \lvert [\tau_{z_j}]_{Vmin}^{Vmax} -z_i \rvert * {1 \over \Delta z} \ )]_0^1 \ p_j(s', \pi(x'))\]

위 식에서 \(Vmin\)과 \(Vmax\)는 [Vman, Vmax]로 범위를 제한한다는 의미이다. 이를 통해 새로운 분포를 기존의 support에 맞춰 옮길 수 있게 된다.

3. loss function

\[D_{KL}(\Phi \hat \tau Z_\theta(s,a) \| Z_\theta (s,a))\]

target value \(\Phi \hat \tau Z_\theta(s,a)\)와 current value \(Z_\theta (s,a)\)의 차이는 분포 간의 차이이기 때문에 MSE는 사용하지 않고, Cross Entropy를 사용한다. Cross Entropy를 사용하는 것은 두 분포 간의 KL Divergence를 줄이는 것과 동일한데, KL Divergence의 경우 분포에 있어 contraction이 보장되지 않기 때문에 수렴이 되지 않을 가능성이 있다. 반면 Wasserstein distance를 이용하면 contraction이 보장되기 때문에 더 좋다고 한다. 하지만 논문에서는 sample transaction만 사용한다는 점에서 wasserstein loss를 구하는 것이 어려워 적용하지 못하고, 그 가능성만 언급하고 있다.

Algorithm

구체적인 알고리즘은 아래와 같다.

C51이라는 이름은 알고리즘에서 하이퍼파라미터인 support의 개수를 51로 하였을 때 SOTA를 기록했기 때문에 붙여진 이름이라고 한다.

additional study

Meaning of Bellman equation/operator

expected bellman equation과 bellman optimality equation은 다음과 같다.

\[Q^\pi(s,a) = E(R(s,a)) + \gamma E_{P, \pi}Q^\pi(s',a')\] \[Q^*(s,a) = E(R(s,a)) + \gamma E_{P} \max_{a' \in A} Q^*(s',a')\]

expected bellman equation은 unique fixed point \(Q^*\)를 갖는데, 이것이 바로 bellman optimality equation이다. 그리고 \(E_{a-\pi^*} [Q^*(s,a)] = \max_a Q^*(s,a)\)이 성립할 때 \(\pi^* \in \Pi\)는 optimal policy가 된다.

bellman operator는 쉽게 말해 bellman equation을 벡터 간의 곱 형태로 표현한 것이라고 할 수 있다. 구체적인 내용은 다음 링크에 정리해두었다. 논문에서는 \(\rm I\!R^{s x a}\) 백터 간 연산의 형태로 bellman operator \(\tau^\pi\)와 bellman optimality operator \(\tau\)를 다음과 같이 정의하고 있다.

\[\tau^{\pi}Q(s,a) = E[R(s,a)] + \gamma E_{P, \pi}[Q(s',a')] \\ \tau Q(s,a) = E[R(s,a)] + \gamma E_{P} \max_{a' \in A}[Q(s',a')]\]

Distributional Bellman Operator

위에서 언급한대로 distributional RL에서는 \(Q\) value를 분포의 기대값으로 구한다. 따라서 각 \((s,a)\)를 평가하기 위해 \((s,a)\)를 각각의 가치에 맞게 분포로 매핑해줘야 한다. 이때 사용되는 것이 \(Z^\pi\)이며, 이를 value distribution이라고 한다.