Enfow's Blog

🦄 About
📚 Posts

논문 제목 : Smooth Adversarial Training

  • Cihang Xie, Mingxing Tan, Boqing Gong, Alan Yuille, Quoc V. Le
  • 2020
  • 논문 링크

Summary

  • Smooth Activation Function이란 Gradient가 연속함수인 경우를 의미한다.
  • Adversarial Training에서 ReLU가 아닌 Smooth한 특성을 가지는 Activation Function을 쓰면 Accuracy를 낮추지 않고도 Adversarial Robustness를 높일 수 있다. 이는 Gradient의 질이 보다 좋기 때문이다.
  • 논문의 실험은 Adversarial Training이라는 특수한 상황에서 진행되었다. 하지만 기본적으로 사용하는 ReLU가 아닌 다른 Activation Function을 사용하면 성능(Accuracy)이 높아질 수 있다는 점을 보이고 있으므로 GELU, CELU와 같은 다른 Activation Function을 사용해보는 것도 고려해 볼 필요가 있다.

Adversarial Training

Adversarial (Machine) Training에 대해 위키에서는 다음과 같이 정의한다.

  • Adversarial machine learning is a machine learning technique that attempts to fool models by supplying deceptive input.

즉 Adversarial Training이란 속임수를 써서 머신러닝 모델을 속일 수 있는지 알아보는 것이라 할 수 있다. 이때 머신러닝 모델을 속이려 하는 것을 Adversarial Attack이라고 하는데, 특히 딥러닝은 이러한 Adversarial Training에 취약하다고 알려져 있다. 이와 관련하여 대표적인 실험으로 Ian Goodfellow 등의 논문 Explaining and Harnessing Adversarial Examples에서 진행한 실험이 있다.

오리지널 판다 이미지를 넣었을 때에 딥러닝 모델은 57.7%의 확률로 판다 이미지로 분류하였으나, 특정한 방식으로 만든 노이즈를 판다 이미지와 합하여 입력으로 전달하니 99.3%의 확률로 긴팔 원숭이로 분류했다는 것을 의미한다. 이러한 문제를 줄이기 위한 방법, 즉 Adversarial Attack으로부터 보다 robust한 모델을 만들기 위한 노력들이 있어왔으나, 논문에서는 지금까지 제시되어온 방법들은 Adversarial Robustness를 위해 Accuracy를 희생했다고 평가한다.

ReLU Weakens Adversarial Training

이와같이 Adversarial Robustness와 Accuracy가 상충관계에 있는 이유에 대해 논문에서는 ReLU를 꼽고 있다. 보다 구체적으로 ReLU는 Non-Smooth한 특성을 가져 Gradient의 질이 상대적으로 좋지 않고, 이로 인해 이러한 문제가 발생한다는 것이다. 논문의 제목처럼 이러한 문제를 해결하기 위해서는 Non-Smooth가 아닌 Smooth한 특성을 가지는 Activation Function을 써야 한다는 것이 논문의 요지라고 할 수 있다.

In this paper, we show that, with SAT(Smooth Adversarial Training), adversarial robustness can be improved for free

이를 보이기 위해 논문에서는 다양한 Adversarial Training을 진행하고 있다.

Adversarial Training Setting

기본적인 Adversarial Training 수식은 다음과 같다.

\[\arg_\theta \min E_{(x, y) \backsim D} [\max_{\epsilon \in S} L(\theta, x + \epsilon, y)]\]

여기서 \(D\)는 원 데이터셋, \(L\)은 loss, \(\epsilon\)은 adversarial perturbation, 즉 원 데이터에 더해주는 noise라고 생각할 수 있다. 즉 수식은 여러 noise 중 loss가 가장 큰 경우를 골라 이것을 사용하여 네트워크를 업데이트하겠다는 것을 의미한다. 이때 논문에서는 Expectation 내부의 \(\max\) 부분을 Inner Maximization Step이라고 하며 Adversarial Example을 만드는 것으로, 외부의 \(\min\) 부분을 Outer Minimization Step이라고 하고 네트워크 파라미터를 업데이트하는 것으로 구분한다.

Smoothness Setting

논문에서는 ReLU를 사용할 때의 Gradient가 좋지 못한 이유로 0에서 Gradient가 급작스럽게 변화한다는 점을 든다.

\[\text{ReLU: } f(x) = \max(0, x)\]

그리고 이것이 문제임을 보이기 위해 ReLU와 매우 유사한 형태를 가지지만 0에서 부드럽게 변화하는 새로운 Activation Function을 아래와 같이 제시한다. 참고로 \(\alpha\)가 커지면 커질수록 ReLU에 가까워진다.

\[\text{Parametric Softplus: } f(\alpha, x) = {1 \over \alpha} \log (1 + \exp (\alpha x))\]

실제로 그래프를 그려보면 다음과 같다. 빨간 선은 \(\alpha = 1\), 보라 선은 \(\alpha = 5\), 검은 선은 \(\alpha = 10\)인 경우를 의미하며 녹색 선이 ReLU이다.

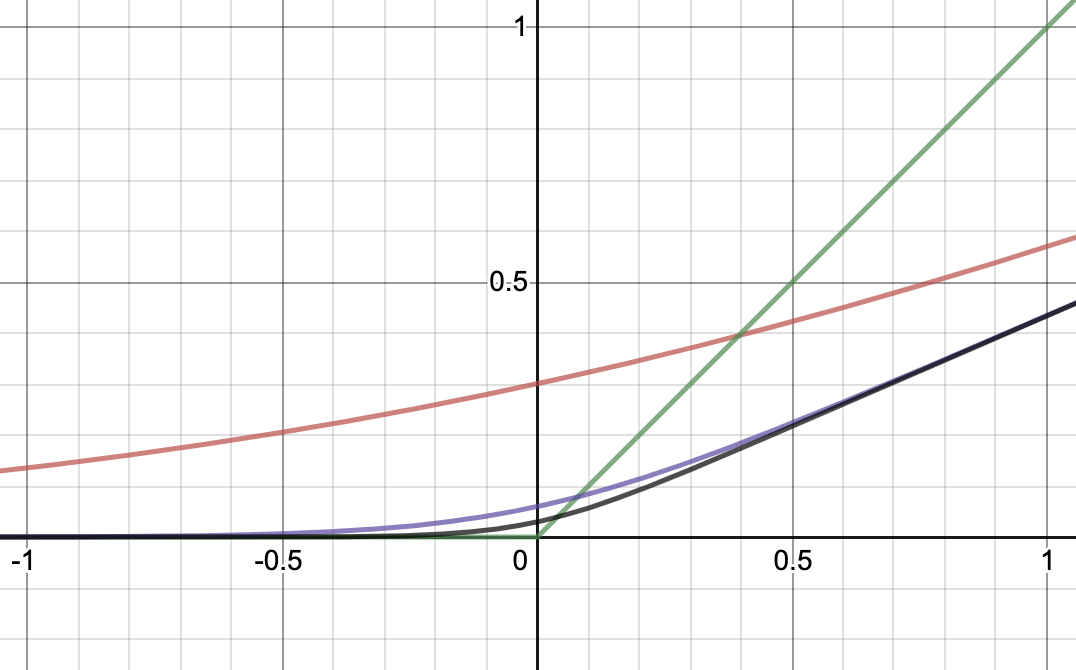
이것의 Gradient를 구해보면 다음과 같이 연속적이라는 것을 알 수 있다. 이러한 점에서 Smooth하다고 하는 것이다.

\[{d \over dx} f(\alpha, x) = {1 \over (1 + \exp (- \alpha x))}\]

Experiment 1: How Gradient Quality Affects Adversarial Training

논문에서는 Inner Maximization Step, Outer Minimization Step 각각에 대해 ReLU를 사용하는 경우와 Parametric Softplus를 사용하는 경우로 하여 총 4가지 실험을 진행했다고 한다. Parametric Softplus를 사용하는 경우에도 실험의 목적이 Activation Function이 Smooth 할 때 Gradient의 질이 좋아지는지 확인하기 위한 것인 만큼 Forward Pass에서는 그대로 ReLU를 쓰고 Backward Pass에서만 Activation Function을 바꾸어 사용했다고 한다.

결과적으로 모든 경우에서 Parametric Softplus를 적용하여 Gradient를 계산했을 때 ReLU만을 사용했을 때보다 Adversarial Robustness가 높았고, Inner Maximization Step에만 적용한 경우를 제외하면 Accuracy 또한 함께 높아진다. 즉 Smooth한 Activation Function을 사용하면 Adversarial Robustness와 Accuracy 간의 trade-off 없이 두 가지를 모두 높일 수 있다는 것이다.

Experiment 2: Adversarial Training with Smooth Activation Functions

첫 번째 실험에서는 smooth하지 않은 ReLU의 특성상 Gradient의 질이 낮은 것이 문제라는 것을 보였다면 두 번째 실험에서는 ReLU를 대신할 만한 Smoothness를 갖춘 Activation Function들을 비교하고 있다. 실험에 사용된 Activation Function은 다음과 같다.

제목 내용
Softplus \(f(x) = \log(1 + \exp(x))\)
Parametric Softplus \(f(x, \alpha) = {1 \over \alpha}\log(1 + \exp(\alpha x))\)
Swish \(f(x) = x \cdot \text{sigmoid}(x)\)
GELU \(f(x) = x \cdot \Phi(x)\)
ELU \(f(x, \alpha) = \eqalign{ &\text{if} (x \geqq 0), \ x \\ &\text{otherwise, } \alpha(\exp(x) - 1) }\)
SmoothReLU \(f(x, \alpha) = \eqalign{ &\text{if} (x \geqq 0), \ x - {1 \over \alpha} \log(\alpha x + 1) \\ &\text{otherwise, } 0 }\)
\[*\Phi(x) \text{ is the cumulative distribution function of the standard normal distribution}\]

여기서 Softplus, Swish, GELU, ELU는 \(x \le 0\)에서 ReLU와 달리 양수를 반환하기 때문에 항상 0을 반환하는 ReLU와는 특성이 다르다고 할 수 있다. 이것이 학습에 미치는 영향을 배제하기 위해 ReLU와 같이 \(x < 0\)에서 항상 0을 반환하면서도 Smooth한 특성을 가지는 SmoothReLU를 추가했다고 한다.

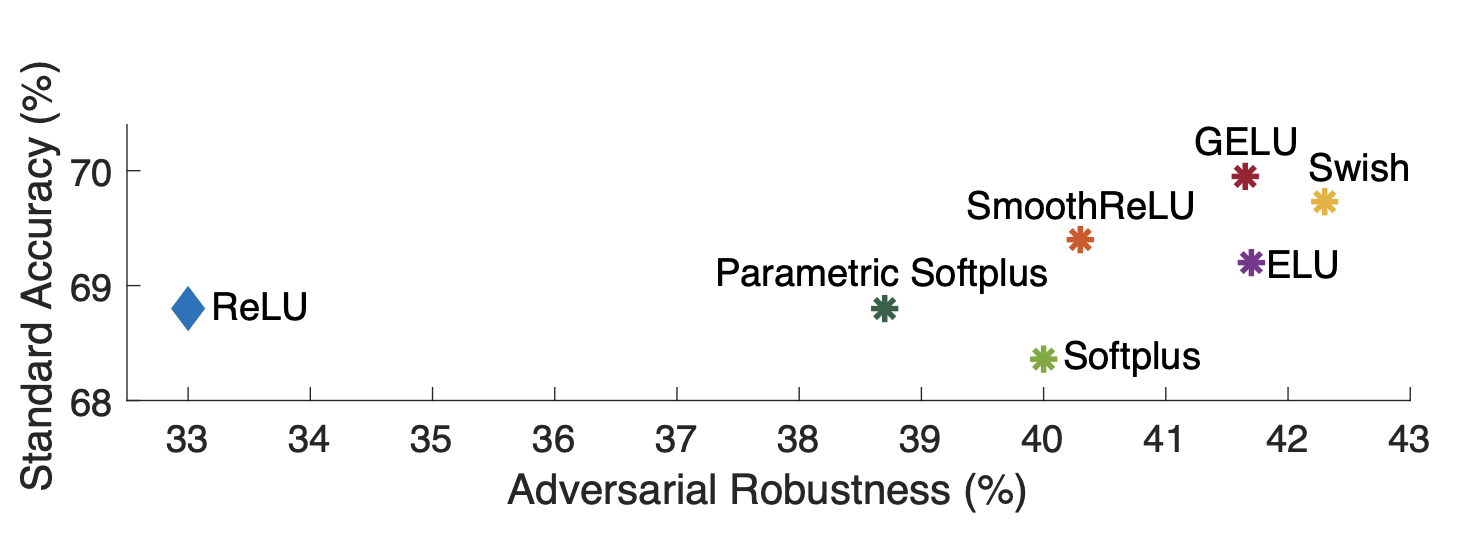
결과는 위와 같이 비교의 기준이 되는 ReLU와 비교해 Adversarial Robustness는 모두 높았으며, Softplus를 제외하면 Accuracy도 모두 높은 것을 알 수 있다.