논문 제목 : Matching Networks for One Shot Learning

• Oriol Vinyals, Charles Blundell, Timothy Lillicrap, Koray Kavukcuoglu, Daan Wierstra
• 2016
• Paper Link

Summary

• 데이터가 적은 상황에서도 충분히 좋은 성능을 낼 수 있도록 Matching Net Model과 Episode Training을 제안한다.
• Matching Net은 LSTM을 통해 Support Set 전체 데이터의 정보를 반영하도록 하고, Attention Mechanism을 적용해 Non-Parametric한 특성을 가지도록 하고 있다. 이를 통해 적은 데이터로도 Fine Tuning 없이 유사한 Task대해 어느 정도 성능이 확보된다.
• Episode Training 이란 Batch Set과 Support Set으로 학습 데이터셋을 나누어 구성하고, 각각을 Episode 단위로 하여 학습을 진행하는 Meta Learning의 학습 방법을 말한다.

Issue of Deep learning

딥러닝의 가장 큰 문제 중 하나는 모델을 학습하는 데에 매우 많은 데이터가 필요하다는 것이다. 이러한 문제의 원인과 관련하여 논문에서는 딥러닝 모델이 가지는 Parametric한 특성으로 인해 대상을 느리게 학습하기 때문이라고 지적한다. 실제로 딥러닝 이외에 머신러닝의 다른 Non-Parametric 방법론들에서는 딥러닝에 있어 중요한 문제이자 한계로 지적받는 Catastrophic Forgetting 없이도 빠르게 학습이 이뤄진다. 이러한 점에서 논문에서는 Non-Parametric 특성을 가지는 모델을 사용하여 새로운 것을 빠르게 학습하면서도 다른 일반적인 example들에 대해서도 어느 정도의 성능을 유지할 수 있는 모델 Matching Nets와 그에 맞는 학습 방법론 Episode Training을 제안하고 있다.

Matching Net

Matching Net은 Task 자체를 학습하는 Meta-Laerning 모델이다. 일반적인 분류문제에서 모델은 (개, 고양이, 거북이, 닭, 코끼리, 양, 돼지, 말)로 이뤄진 데이터셋을 분류하는 하나의 Task를 학습하게 된다. 이 경우 Test에서 Training Set에 포함되어 있는 동물들에 대해서는 정확하게 분류할 가능성이 높지만 그렇지 않은 아르마딜로나 티라노사우루스는 오분류할 가능성이 매우 높다. 이러한 문제를 (개, 고양이), (거북이, 닭), (코끼리, 양), (돼지, 말) 등으로 나누어 여러 개의 분류 문제를 만들고, 특정 데이터를 분류하는 것이 아닌 ‘분류’ 그 자체를 모델이 학습하도록 하는 것도 가능하다. 이와 같이 하나의 Task가 아닌 여러 개의 Task를 Meta적으로 학습한다고 하여 이와 같은 방법에 대한 연구 분야를 Meta-Learning이라고 한다.

논문의 제목에도 나오는 One-Shot Learning, 혹은 Few-Shot Learing이란 각 Task를 학습하는데에 사용되는 Training Set(Support Set)의 개수를 의미한다. 위의 예시대로라면 개, 고양이, 거북이, 닭, 코끼리, 양, 돼지, 말 각각 1장씩으로 Training Set을 구성한다면 One-Shot Learning, 하나보다는 많지만 적은 숫자로 구성하게 되면 Few-Shot Learning이라고 부르는 식이다. 참고로 위키에서는 다음과 같이 One-Shot Learning을 정의하고 있다.

• One-shot learning aims to learn information about object categories from one, or only a few, training samples/images.

Set-to-Set Framework

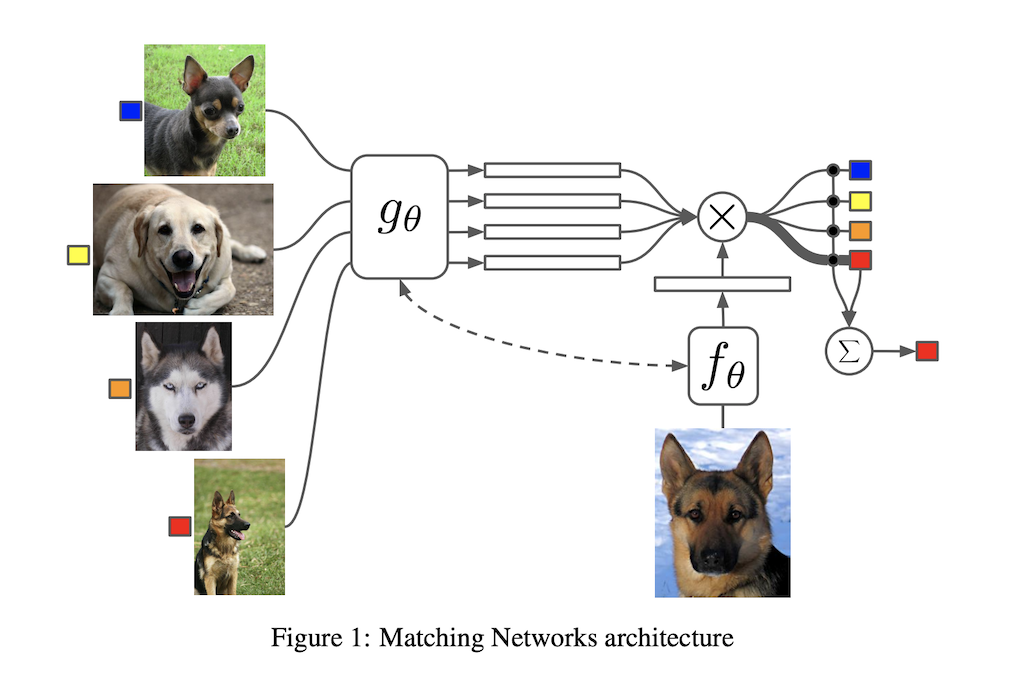
Matching Net의 가장 큰 특징은 모델을 \(P(B \lvert A)\)로 표현할 때 Seq2Seq에서는 \(A, B\)가 Sequence였다면 여기서는 Set으로 본다는 것이다. 이를 논문에서는 set-to-set framework라고 하며 Matching Net은 이를 적용하여 모델이 본 적 없는 Test Data를 분류하는 모델이라고 할 수 있다.

따라서 Matching Net의 입력은 데이터 집합이 된다. Meta Learning에서는 이와같이 학습에 사용되는 Task 단위의 데이터셋을 Support Set이라고 하는데, \(i\)개의 이미지를 분류하는 Task가 \(k\)개 있는 Support Set은 다음과 같이 정의할 수 있다.

\[\text{Support Set } S = \{ (x_i, y_i) \}_{i=1}^k\]

그리고 이러한 Support Set을 사용하여 어떤 test example \(\hat x\)를 그에 맞는 \(\hat y\) 분류하는 Classifier \(C_S(\hat x)\)를 만들고자 한다면 다음과 같이 모델을 표현할 수 있다.

\[P(\hat y \lvert \hat x, S)\]

모델을 조금 더 구체적으로 표현하면 다음과 같다. 여기서 \(a(\cdot)\)은 Attention Mechanism을 의미한다. 즉 \(\hat x\)와 \(x_i\)가 유사하면 유사할수록 그 값이 커지게 된다.

\[\hat y = \Sigma_{i=1}^k a(\hat x, x_i) y_i\]

이때 \(a\)가 \(X \times X\) 상의 Kernel이고 Support Set \(\{ x_i \}\) 중에서 유사도가 \(b\)번째 이내에 들지 못하는 \(x_k\)에 대해서 \(a(\hat x, x_k) = 0\)가 성립한다면 모델이 Kernel Density Estimation(KDE)으로서 Non-Parametric한 특성을 가진다고 할 수 있다.

Non-Parametric Density Estimation

Non-Parametric Density Estimation이란 Data에 대해 어떠한 가정도 하지 않은 채 주어진 Data 그 자체만으로 어떤 확률분포를 추정하는 것이다. Parametric Density Estimation과 대조되는 개념으로 이해하면 되는데, Parametric Density Estimation의 가장 쉬운 예시는 주어진 Data의 분포가 가우시안 분포를 따른다고 가정하고, Data의 평균과 표준편차를 Parameter로 하는 정규 분포로 추정하는 것이다. 여기서 Data가 정규분포를 따른다고 가정하는 것이 Parametric Density Estimation의 가장 큰 특징이다. Non-Parametric Density Estimation에서는 당연히 이러한 가정이 없다.

Non-Parametric한 Machine Learning 방법론 중 가장 대표적인 것으로 KNN(k-Nearlist Neighbor)이 있다. KNN을 떠올리며 위의 식과 그 가정, \(b\) 번째 이후는 \(a(\cdot)\)의 값을 0으로 하겠다는 것을 생각해보면 위의 식이 결국에는 KNN과 의미적으로 동일하다는 것을 알 수 있다. 다시말해 유사도 공간 상에서 \(\hat x\)와 \(k - b\) 번째로 가까운 \(x_i\)에 대해서만 고려하여 \(\hat y\)를 결정하겠다는 것을 의미하며, 이러한 점에서 위 식을 Non-Parametric한 특성을 가진다고 하는 것이다.

Attention Kernel

Attention Mechanism을 구현하는 방식은 가장 쉽게 그리고 많이 사용되는 Dot Product 외에도 다양하게 존재한다. 논문에서 보여주는 예시는 Cosine Similarity \(c(\cdot)\)에 Softmax를 적용하는 방법이다(Matching Net에서 사용하는 방법은 아니다).

\[a(\hat x, x_i) = {e^{c(f(\hat x), g(x_i))} \over \Sigma_{j=1}^k e^{c(f(\hat x), g(x_i))}}\]

여기서 \(f, g\)는 Neural Net으로 구현되는 Embedding Function으로서, 각각 \(\hat x\)와 \(x_i\)를 임베딩하는 역할을 수행한다. 참고로 두 Neural Net으로는 VGG나 Inception을 사용한다고 한다.

Full Context Embeddings

그런데 \(f, g\)에 대해 논문에서는 단순히 \(\hat x\)와 \(x_i\)를 하나씩 받는 것은 근시안적(myopic)이라고 지적한다. 왜냐하면 모델이 \(P(\cdot \lvert \hat x, S)\)에서 확인할 수 있듯이 Support Set \(S\) 전체에 Conditioned 되어 있어 Support Set을 구성하는 모든 \(x_i\)를 개별적으로 받는다고 할지라도 전체 \(S\)에 대한 정보는 얻기 힘들기 때문이다. 그리고 Support Set \(S\)에 따라 \(f(\hat x)\) 또한 다르게 임베딩 되어야 할 필요가 있다.

따라서 논문에서는 다음과 같이 LSTM을 이용하여 \(f\)를 정의한다.

\[f(\hat x, S) = \text{attLSTM} (f'(\hat x), g(S), K)\]

이때 \(f'\)는 VGG와 같은 Neural Net이고, 하이퍼 파라미터 \(K\)는 Process를 의미하는데 Process란 다음과 같은 일련의 과정을 지칭한다.

\[\eqalign{ \hat h_k, c_k &= \text{LSTM} (f'(\hat x), [h_{k-1}, r_{k-1}], c_{k-1})\\ h_k &= \hat h_k + f'(\hat x) + f'(\hat x)\\ r_{k-1} &= \Sigma_{i=1}^{\lvert S \rvert} a(h_{k-1}, g(x_i))g(x_i)\\ a(h_{k-1}, g(x_i)) &= \text{softmax}(h_{k-1}^Tg(x_i)) }\]

\(g(x_i, S)\)는 다음과 같이 정의된다.

\[\eqalign{ & g(x_i, S) = \overrightarrow h_i + \overleftarrow h_i + g'(x_i) \\ & \overrightarrow h_i \overrightarrow c_i = \text{LSTM}(g'(x_i), \overrightarrow h_{i-1}, \overrightarrow c_{i-1})\\ & \overleftarrow h_i \overleftarrow c_i = \text{LSTM}(g'(x_i), \overleftarrow h_{i-1}, \overleftarrow c_{i-1})\\ }\]

이와 같이 LSTM을 사용하여 전체 Support Set \(S\)의 맥락에서 개별 데이터 \(x_i\)를 이해하도록 할 수 있다고 한다.

Episode Training

위와 같이 모델을 만들고 일반적인 방법에 따라 Mini Dataset들을 일괄적으로 학습시키면 잘 되지 않는다. 이와 관련하여 논문에서는 다음과 같은 표현이 등장한다.

• Test and train conditions must match. Thus to train our network to do rapid learning, we train it by showing only a few examples per class, switching the task from minibatch to minibatch, much like how it will be tested when presented with a few examples of a new task.

Matching Net의 목표는 한 번도 본적 없는 Task가 Test Time에 들어와도 적절히 대처하는 것이다. 따라서 Test and train conditions must match를 만족하기 위해서는 Training 또한 이와 매우 유사하게 이뤄져야 한다. 이를 위해 Train set을 다음과 같이 구성하게 된다.

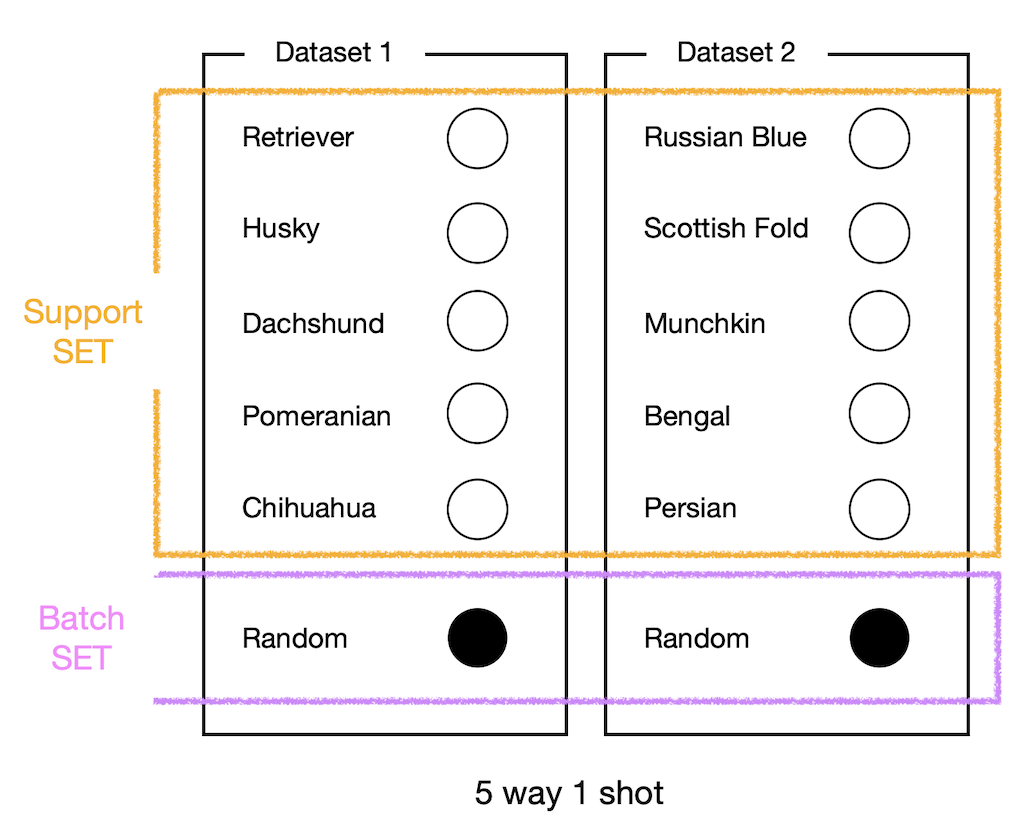
첫 번째 에피소드에는 강아지의 종류를 입력으로 받고 그에 따라 loss를 계산한 뒤 모델을 학습하고, 똑같은 방식으로 두 번째 에피소드에는 고양이를 분류하고 학습하는 식으로 Training 하는 것을 Episode Training 이라고 한다. 전체 Task \(T\)에서 추출한 Dataset \(L\)이 있고, 여기서 다시 Support Set \(S\)와 Batch Set \(B\)를 추출한다면 다음과 같이 업데이트 식을 정의할 수 있다.

\[\theta = \arg \max_\theta E_{L \backsim T} [ E_{S \backsim L, B \backsim L} [\Sigma_{(x,y) \in B} \log P_\theta (y \lvert x, S)] ]\]

앞서 언급한대로 모델이 Non-Parametric 한 특성을 가지므로 Test Set에 대해 어떠한 Fine Tuning도 필요하지 않다는 장점을 가진다. 물론 Test로 들어오는 Task가 학습에 사용된 전체 Task의 분포와 크게 다른 경우 성능은 떨어질 수 밖에 없다.