Enfow's Blog

🦄 About
📚 Posts

Chain-of-Thought Prompting Elicits Reasoning in Large Language Models

Summary

  • Chain-of-Thought Prompting이란 Few-shot으로 <Input, Chain-of-Thought, Output> 을 함께 넣어주는 방법을 말한다.
  • Chain-of-Thought 란 최종 결과에 도달하는 과정에서 필요한 일련의 추론 과정을 말한다.
  • Chain-of-Thought는 Reasoning 문제에 효과적이며, 특히 모델의 크기가 크면 클수록, 문제가 복잡하면 복잡할수록 성능 향상의 폭이 크다.

Reasoning Task

Reasoning Task 란 말 그대로 추론이 필요한 작업들을 말한다. 자연어의 무한한 가능성을 고려해 볼 때 Reasoning Task의 종류 또한 무한히 많을 수밖에 없는데, 대표적으로 아래 세 가지 유형의 문제들을 생각해 볼 수 있다.

Arithmetic Reasoning

숫자를 계산하는 문제들을 말한다.

Q: Roger has 5 tennis balls. He buys 2 more cans of tennis balls. Each can has 3 tennis balls. How many tennis balls does he have now?
--------------------------------
A: The answer is 11.

Commonsense Reasoning

일반적인 상식과 관련된 문제들을 말한다.

Q: Sammy wanted to go to where the people were. Where might he go? Options: (a) race track (b) populated areas (c) desert (d) apartment (e) roadblock
--------------------------------
A: The answer is (b).

Symbolic Reasoning

사람이 만들어낸 규칙과 관련된 문제들을 말한다.

Q: Take the last letters of the words in “Lady Gaga” and concatenate them.
--------------------------------
A: The answer is ya.

175B의 크기를 가진 GPT-3이 강력한 성능을 입증한 이후 Scaling Law, 즉 모델의 크기를 키우면 키울수록 그 성능이 올라가는 경향이 있다는 것은 보편적으로 받아들여지고 있다. 하지만 다수의 Benchmark 에서 LLM 모델들이 비약적인 성능 향상을 보였으나, Reasoning Task에서 만큼은 성능 향상을 보여주지 못했다.

논문에서는 Chain-of-Thought Prompting을 적용하게 되면 기존 모델들로도 Reasoning Task에서 성능이 크게 좋아질 수 있다고 주장한다. 그렇다면 Chain-of-Thought Prompting 이란 무엇일까.

Chain-of-Thought Prompting

어떤 사람이 복잡한 추리(Reasoning)가 요구되는 작업을 수행한다고 해보자. 이 경우 대개 최종 결론에 도달하기 위해 여러 개의 중간 질문에 대한 답을 하나씩 찾아가는 식으로 진행하게 된다. Chain-of-Thought Prompting은 이와 같이 최종 결과에 도달하는 과정에서 필요한 일련의 추론 과정들을 프롬프트로 함께 제공하는 것을 뜻한다. 위의 Arithmetic Reasoning 예시를 기준으로 보면 아래와 같이 작성하는 것이다.

Q: Roger has 5 tennis balls. He buys 2 more cans of tennis balls. Each can has 3 tennis balls. How many tennis balls does he have now?
--------------------------------
CoT: Roger started with 5 balls. 2 cans of 3 tennis balls each is 6 tennis balls. 5 + 6 = 11.
--------------------------------
A: The answer is 11.

Methodology

방법은 간단하다. 일반적인 Language Model Dataset은 Input과 그에 맞는 바람직한 Output의 쌍으로 되어 있다. 여기에 Output이 어떻게 결정되었는지에 대한 설명이라 할 수 있는 Chain-of-Thought을 추가하여 Few-Shot Leanring 에 사용하는 것이다. GPT-3 논문에서 제시된 일반적인 Few-Shot Learning이 Input과 Output Pair를 Demonstration으로 넣어주었다면 여기서는 Chain-of-Thought도 추가하여 <Input, Chain-of-Thought, Output> Triple로 넣어주는 것이다.

기존 방식(Standard Prompting)과 비교하여 보면 보다 쉽게 이해할 수 있다.

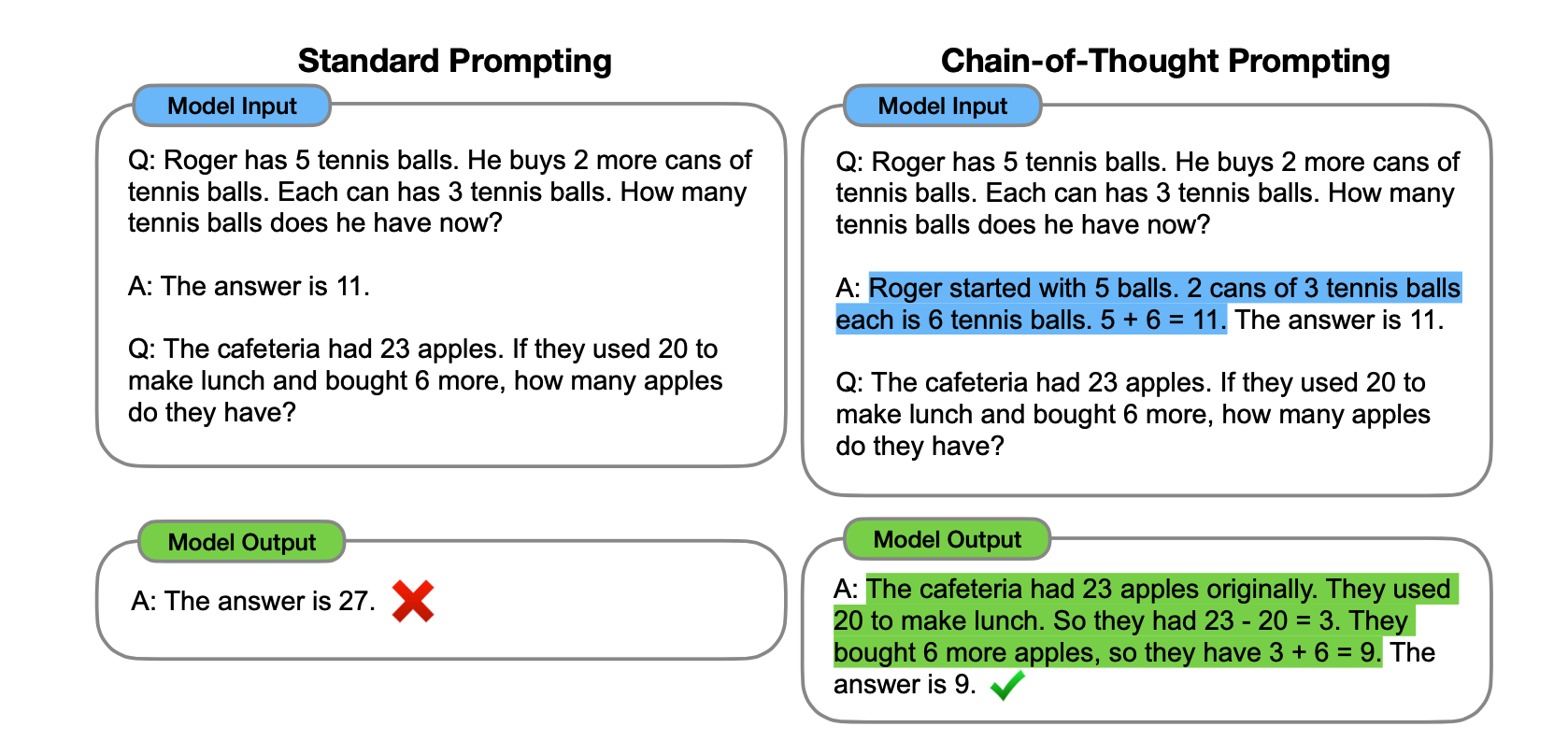
cot-compare-standard-and-cot

이러한 Chain-of-Thought는 다음 두 연구의 영향을 받았다고 한다.

1. Rationale-augmented training/fine-tuning

Input-Output Pair와 더불어 Output이 결정된 이유, 설명(Rationale) 을 함께 학습하는 방법을 말한다. arithmetic reasoing 의 경우 최종 결론에 도달하는 데에 필요한 추론 과정을 자연어로 생성하도록 학습함으로써 보다 정확한 답을 얻을 수 있다는 것이 앞선 연구에서 확인되기도 하였다. 하지만 학습에 사용하려면 다량의 데이터가 필요한데, 고품질의 Rationale을 확보하는 것이 어렵다는 점에서 어려움이 있다.

2. Few-Shot Prompting

해결하고자 하는 문제와 유사한 문제들을 프롬프트에 함께 제공(Few-Shot Learning)하게 되면 다양한 Task에서 성능이 높아지는 것 또한 확인되었다. 하지만 단순히 Demonstration 을 제공하는 방법만으로는 Reasoning Task 에서는 확실한 성능 향상을 보여주지 못했다.

Chain-of-Thought 는 위 두 가지 방법의 장점을 조합하여 서로가 가지는 단점을 완화한다. Rationale-augmented training 의 단점이 학습에 사용할 만큼의 데이터를 확보하기 어렵다는 것이었다면 이를 Few-Shot Learning 으로 대체하여 소수의 데이터 만으로도 가능하도록 만들고, 반대로 Few-Shot Learning 이 Reasoning 에 탁월치 못했다는 단점을 Demonstration 으로 Rationale 을 함께 주입하는 식으로 보완하는 것이다.

방법 단점 해결
Rationale-augmented training 고품질의 데이터 확보에 어려움 소수의 Few-Shot 데이터로 대체
Few-shot learning Reasoning Task 해결에 어려움 Rationale 을 함께 주입하여 성능 향상

Advantages of Chain-of-Thought

Chain-of-Thought 는 다음과 같은 장점을 가진다.

  1. 하나의 문제를 Multi-Step Problem 으로 만들어 해결하다보니 Reasoning Step이 추가되고 결과적으로 더욱 많은 연산을 하게 된다.
  2. Interpretable Window 가 함께 출력된다. 따라서 어느 과정에서 잘못된 추리가 이뤄졌고, 최종적인 답이 잘못된 원인이 무엇인지 아는 데에 도움이 된다.
  3. Math Word Problem, Commonsense Reasoing 등의 문제를 푸는 데에 도움이 된다.
  4. Few-Shot Prompting 으로 몇 개의 Chain-of-Thought 의 예시를 제공하는 것만으로도 이미 만들어진 모델이 Chain-of-Thought 를 할 수 있도록 유도할 수 있다.

Experiments

Reasoning task에 대한 Chain-of-Thought의 효과성을 측정하기 위해 세 가지 Task, Arithmetic Reasoning, Commonsense Reasoning, Symbolic Reasoning 에 대한 Benchmark dataset들을 선정하고 실험을 진행했다. 일반적인 Language Model Benchmark Dataset 에는 Chain-of-Thought 에 해당하는 부분이 포함되어 있지 않기 때문에 논문의 주요 저자들이 직접 작성했다고 한다. 구체적인 각 Task 별 예시는 아래와 같다.

cot-examples-of-triples

기존과 같이 Input-Output Pair 만을 사용하는 방법과 성능을 비교하기 위해 기존 방법을 Standard Prompting 으로, 논문에서 제안하는 방법을 Chain-of-Thought Prompting 으로 하여 비교하였다.

1. Arithmetic Reasoning

GSM8K, SVAMP, MAWPS 등 총 5개의 Benchmark Dataset 에 대해 실험을 진행하였다. Standard Prompting 에서는 GPT-3 논문에서 제안된 few-shot prompting 을 사용하였고, Chain-of-Thought Promting 에서는 few-shot 을 넣어줄 때 Chain-of-Thought 도 함께 입력으로 넣어주었다. Demonstration 의 갯수는 8개로 진행했다.

Model Size

모델의 크기에 따라 실험을 진행하였고, 일부의 실험 결과는 다음과 같다.

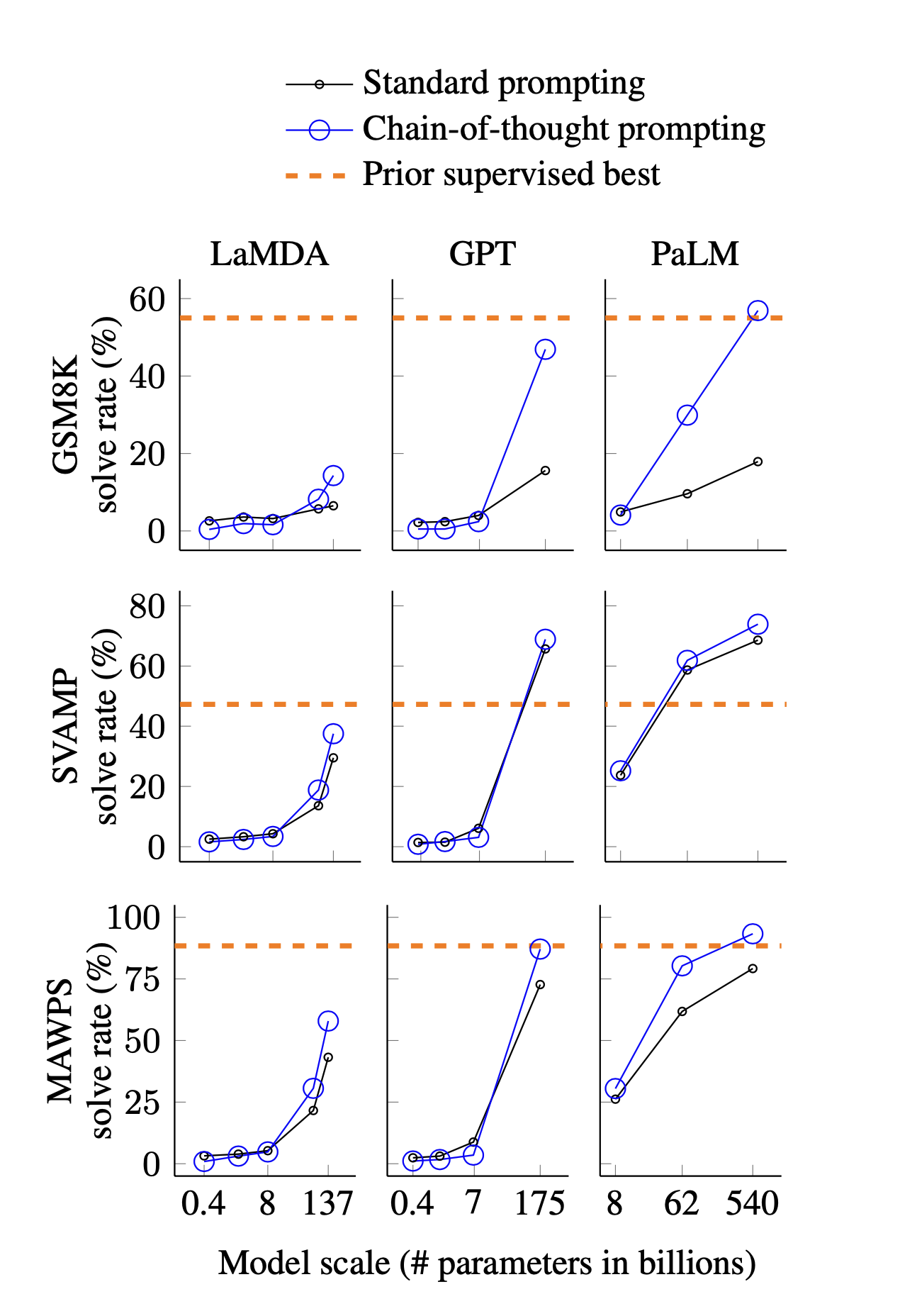
cot-arithmetic-reasoning-result-1

전체적으로 볼 때, 모델의 크기가 커짐에 따라 성능이 좋아지고, Chain-of-Thought 로 인한 증가 폭 또한 커짐을 알 수 있다. 특히 GPT-3 175B와 PaLM 540B 의 경우 많은 데이터 셋에서 기존에 최고 성능을 보이던 Task-Specific Fine-Tuning 모델보다 더욱 높은 점수를 보여주었다(SoTA).

Robustness(annotator)

Few-shot Learning 에서는 examplar의 조합에 따라 성능이 크게 달라질 수 있다(링크). Chain-of-Thought에서도 유사한 문제가 발생할 가능성은 충분하며, 특히 프롬프트를 작성하는 Annotator에 따라 성능이 달라질 수 있다. 이를 확인해보기 위해 논문의 세 저자들은 각각 독립적으로 프롬프트로 사용할 Chain-of-Thought 를 작성하여 실험을 진행하였다.

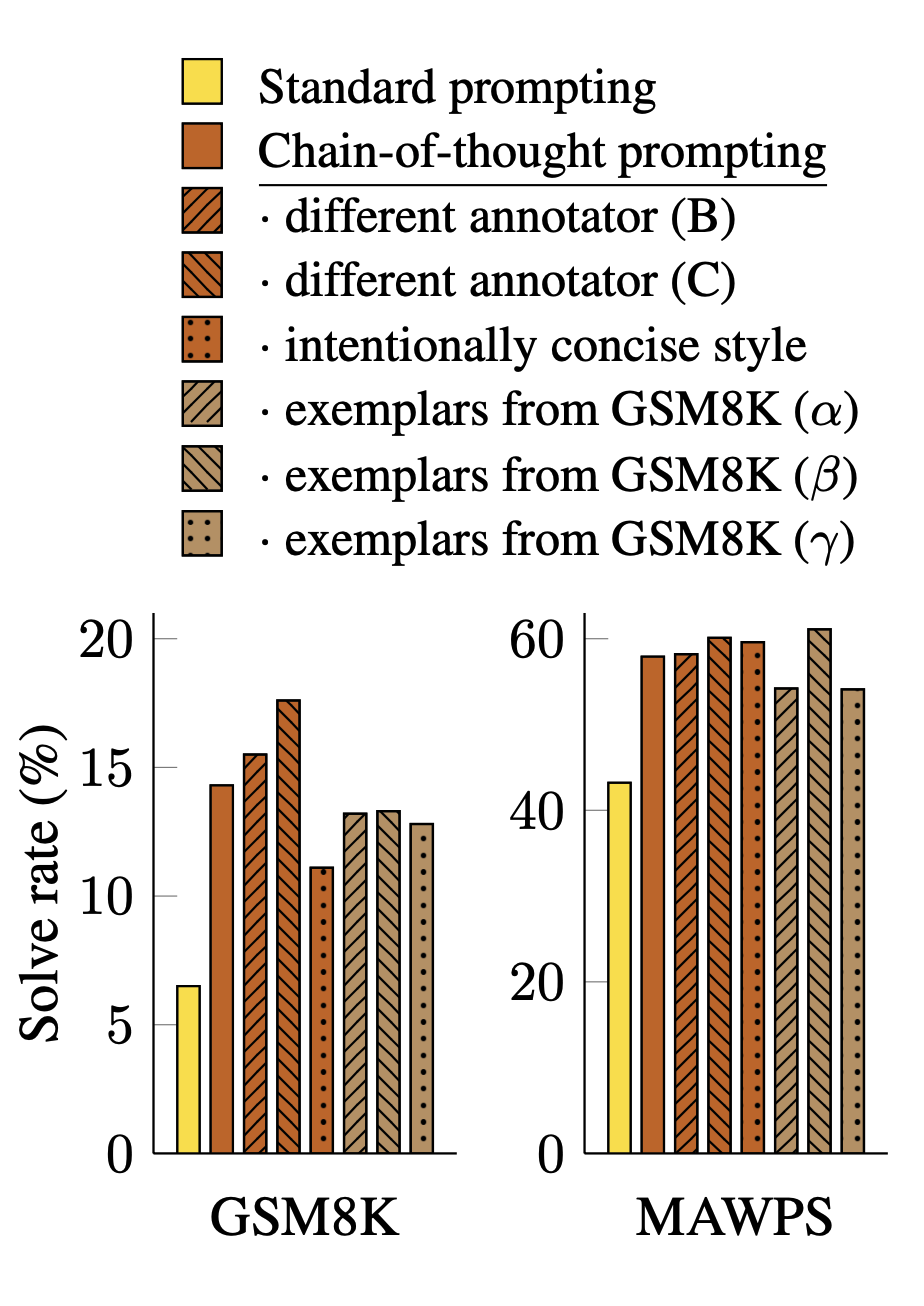
cot-arithmetic-reasoning-result-2

Annotator에 따라 성능의 차이가 존재하나, 베이스라인인 Standard Prompting과 비교해 볼 땐 모두 더 높은 점수를 기록하였다. 이러한 점에서 Chain-of-Thought 으로 인한 성능의 증가는 프롬프트의 스타일과는 개별적으로 이뤄진 것이라 할 수 있다.

2. Commonsense Reasoning

CSQA, StrategyQA 등 5개의 Benchmark Dataset을 활용하였다. 기본적으로 Arithmetic Reasoning의 실험 방식과 크게 다르지 않았다.

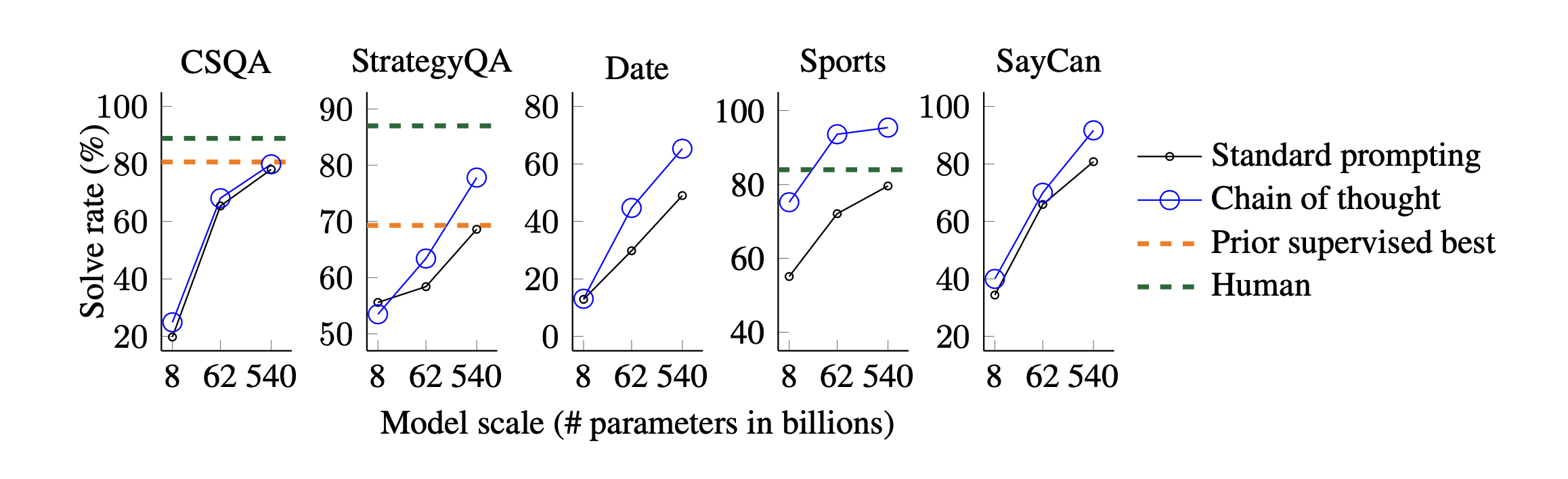
cot-commonsense-reasoning-result-1

실험 결과 또한 모델의 크기가 커질수록 성능이 좋아진다는 점에서 Arithmetic Reasoning 의 실험 결과와 유사했다.

3. Symbolic Reasoning

Symbolic Reasoning 은 사람에게는 쉽지만 Language Model 은 어려워하는 대표적인 문제 유형 중 하나이다. 여기서는 다음 두 가지 Task 를 주로 다루었다.

Last letter concatenation

이름에서 뒷글자만 딴 단어를 생성하는 문제

“Amy Brown”
→ “yn”

Coin flip

동전 뒤집기의 결과를 예측하는 문제

A coin is heads up. Phoebe flips the coin. Osvaldo does not flip the coin. Is the coin still heads up?”
→ “no”

In-Domain & Out-Domain

또한 In-Domain 실험과 더불어 Out-of-Domain(OOD) 실험도 진행하고 비교하였다. 여기서 In-Domain이란 Few Shot 의 Demonstration과 실제 Evaluation이 동일한 복잡도로 구성된 경우를 말한다. Out-Domain 은 그와 반대로 두 개가 서로 다른 복잡도를 가지는 경우를 말한다. Language Model이 입력과 동일한 step 을 밟으면 해답에 이를 수 있는 In-Domain 문제가 일반적으로 보다 쉬운 문제로 받아들여진다.

Last letter concatenation 에서는 Demonstration 에서는 2개 단어로 구성된 이름을, 실제 문제에서는 3~4개의 단어로 구성된 이름을 사용하는 것으로 구현하였고, Coin flip 에서는 flip 하는 횟수를 늘리는 방식으로 구현하였다.

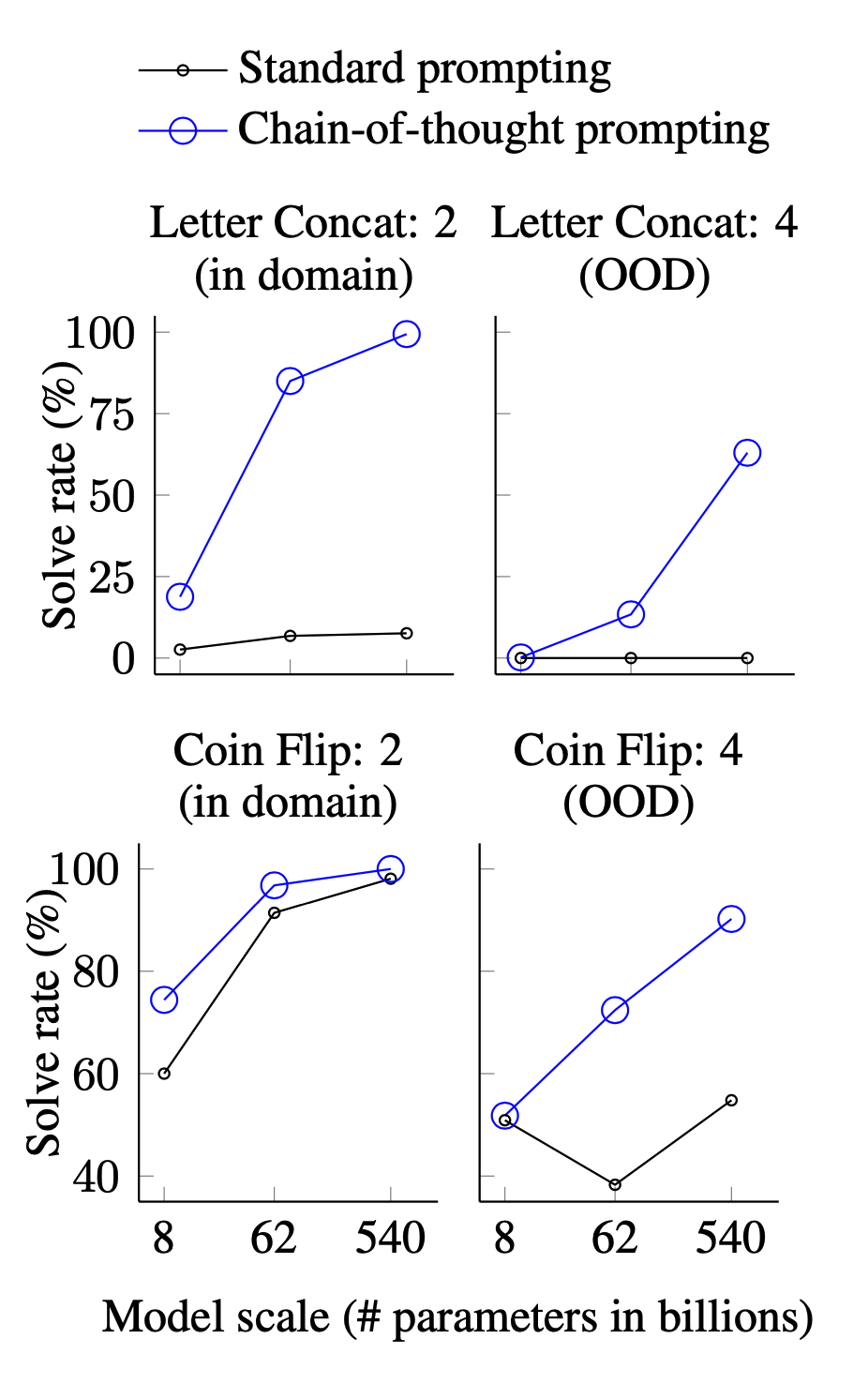
cot-symbolic-reasoning-result-1

In-Domain 문제에서는 PaLM 540B 모델을 기준으로 두 문제에 대해 각각 7.6% -> 99.4%, 98.1 -> 100% 로 스코어가 증가하여, Chain-of-Thougth 가 매우 탁월하게 작용함을 보여주었다. OOD 문제에서는 완벽하게 풀어내지는 못하였지만 비약적인 성능 향상을 보여주었다.

Results

이상의 세 가지 Task에 대한 실험 결과를 종합해보면 다음과 같다.

1. The scale of the model still matters in Chain-of-Thought

Chain-of-Thought에 의한 효과는 모델의 크기가 크면 클수록 보다 강력했다. 특히 크기가 너무 작은 경우(10B)에는 Standard Prompting 과 비교해 볼 때 성능이 오히려 떨어지기도 했다. 적어도 100B 이상은 되어야 Chain-of-Thought가 효과적이라 할 수 있다.

이것의 이유를 알아보기 위해 논문에서는 PaLM 62B 모델이 오답을 만들어낸 경우를 분석하여 semantic understanding(20 errors), one step missing(18 errors), other errors(7 errors) 세 가지로 분류하였다. 이후 540B 모델에 대해서도 동일한 실험을 진행하여 어떤 분류의 error 들이 얼마나 감소하였는지 아래와 같이 정리하였다.

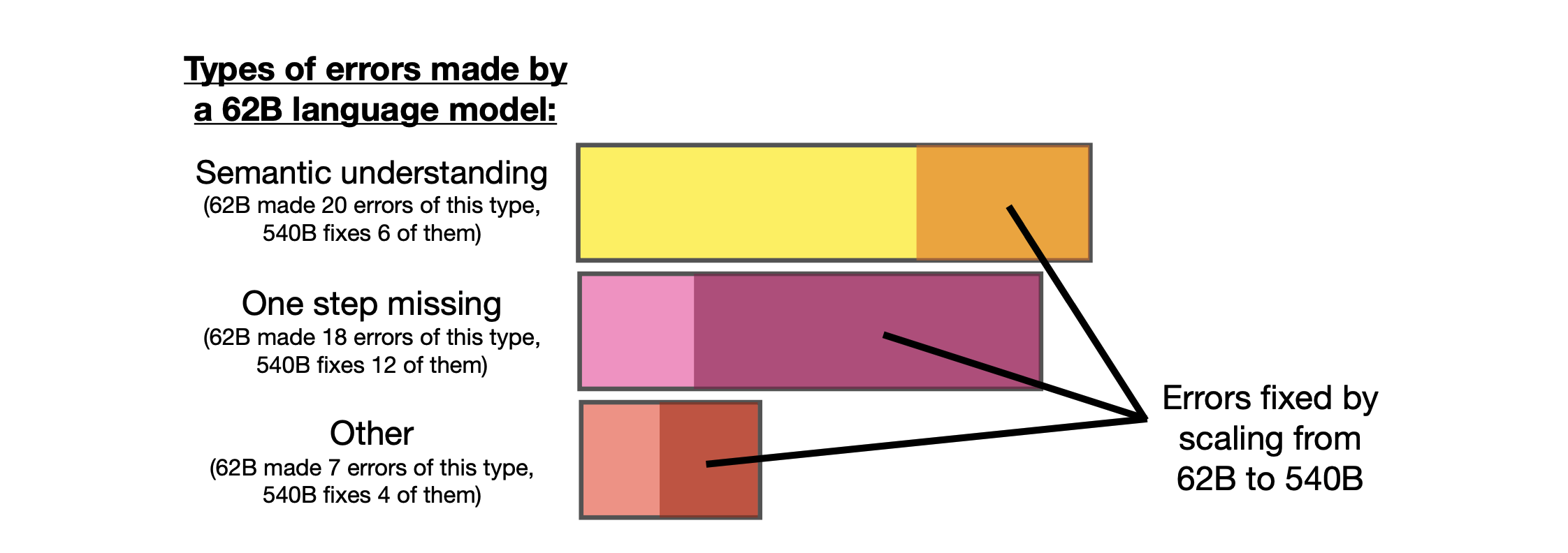
cot-65b-540b-error

작은 모델이 해결하지 못한 문제들을 큰 모델은 일부 잘 해결하였다는 점에서 성능이 보다 높아졌음을 알 수 있다. 나아가 작은 모델들이 실패한 결과들을 분석해보면 다음과 같은 특성을 보였다.

  • Small model은 쉬운 symbol mapping task도 실패한다.
  • Small model 은 arithmetic operation 능력이 낮다. 모델의 크기가 일정 수준 이상이 되어야 이러한 능력이 생기는 것으로 보인다.
  • Small model 은 최종 결과를 생성하는 것에 실패하는 경우가 많았다.

이러한 점에서 문맥을 이해하는 능력과 논리적인 추론을 하는 능력은 모델의 크기가 커짐에 따라 얻는 능력이라고 추정해 볼 수 있다.

2. Make it solve complicated problems better

Chain-of-Thought 를 사용함으로써 복잡한 문제에 대해 더욱 큰 성능 향상을 보여주었다. Arithmetic Reasoning Task에서 GSM8K 데이터 셋에 대해 GPT와 PaLM의 성능이 크게 좋아졌다. GSM8K는 기존 모델들의 성능이 가장 좋지 못했다는 점에서 가장 어려운 문제라고 할 수 있다. 반면 해결에 적은 추론만이 필요한 MAWPS 데이터 셋의 경우 최고 성능의 모델에 대해서도 성능 증가가 그렇게까지 크지는 않았다.

3. Chain-of-Thought demonstrates robustness and generalizability

논문에서는 Chain-of-Thought가 여러 상황에서도 효과적이라는 것을 입증하기 위해 다양한 실험을 추가적으로 진행하였다. 우선 Annotator, 즉 Chain-of-Thought를 작성하는 사람의 스타일에 따른 성능의 차이를 확인하였는데, Annotator에 상관 없이 Standard Prompting에 비해 높은 성능을 보였다는 점에서 Chain-of-Thought의 질이 충분히 좋다면 성능 향상을 기대해 볼 수 있다는 것을 보여주었다.

또한 Out-of-Domain 환경에서도 실험을 진행하였고, 이 또한 다양한 셋팅에서 Standard Prompting 에 비해 성능이 높게 유지되었음을 확인하였다.

Appendix: Pre-Trained Models and Benchmark datasets

Pre-Trained Models

Pre-Trained model로는 다음과 같은 모델들을 주로 사용하였다.

  1. GPT-3(Brown et al., 2020) - 350M, 1.3B, 6.7B, 175B
  2. LaMDA(Thoppilan et al., 2022) - 422M, 2B, 8B, 68B, 137B
  3. PaLM - 8B, 62B, 540B
  4. UL2(Tay et al., 2022) - 20B
  5. Codex(Chen et al., 2021)

Arithmetic Reasoning

  1. the GSM8K benchmark of math word problems (Cobbe et al., 2021)
  2. the SVAMP dataset of math word problems with varying structures (Patel et al., 2021)
  3. the ASDiv dataset of diverse math word problems (Miao et al., 2020)
  4. the AQuA dataset of algebraic word problems
  5. the MAWPS benchmark(Koncel-Kedziorski et al., 2016)

Commonsense Reasoning

  1. CSQA(Talmor et al., 2019)
  2. StrategyQA(Geva et al., 2021)
  3. Date Understanding(BIG-bench collaboration, 2021)
  4. Sports Understanding(BIG-bench collaboration, 2021)
  5. SayCan dataset(Ahn et al., 2022)

Reference