논문 제목 : Relational Inductive Biases, Deep Learning, and Graph Networks
- Peter W. Battaglia, Jessica B. Hamrick, Victor Bapst 등
- 2018
- Paper Link
- Vedio
Summary
- Inductive Bias란 Training에서 보지 못한 데이터 대해서도 적절한 귀납적 추론이 가능하도록 하기 위해 알고리즘(모델)이 가지고 있는 가정들의 집합으로 정의된다.
- 문제(데이터)의 특성에 맞게 적절한 Inductive Bias를 가지는 알고리즘을 사용해야 높은 성능을 낼 수 있는데, CNN은 Locality와 Transitional Invariance한 특성을 RNN은 Sequentiality와 Temporal Invariance한 특성을 가진다.
- Graph를 구성하는 Node와 Edge들은 모두 순서가 없는 Set이며, 이러한 점에서 Graph를 잘 다루기 위해서는 Permutational Invariance한 특성을 가지는 알고리즘이 필요하다. 논문에서는 이와 관련하여 일반적으로 사용할 수 있는 Graph to Graph Framework인 Graph Network(GN)을 제시한다.
Inductive Bias
딥러닝 모델에는 다양한 기본 구조들이 존재한다. 가장 단순하면서도 기본적인 구조라고 할 수 있는 Fully Connected Network(FCN), 이미지를 다루는 분야에서 많이 사용되는 Convolution Neural Network(CNN), 언어를 비롯한 시계열 데이터에서 효과적인 Recurrent Neural Network(RNN) 등이 가장 널리 알려진 구조들이다. 특정 분야에서 가장 효과적이라고 알려진 딥러닝 모델들은 결국 이러한 기본 구조들을 적절하게 조합한 결과라고 할 수 있다.
사실 위에서 언급한 각각의 구조들이 가지는 상대적인 장점들은 잘 알려져 있다. 이미지가 대표적이라고 할 수 있을텐데, 기본적인 MNIST Classification에서 시작하여 Semantic Segmentation, Facial Recognition까지 이미지를 다루는 대부분의 딥러닝 모델들은 모두 CNN을 사용한다.
Inductive Bias는 이와 같이 CNN이 왜 이미지를 다루는 작업에 있어 강점을 보이는지에 대한 설명이라고 할 수 있다. 여기서 말하는 Inductive Bias는 다음과 같이 정의된다(Springer).
- In machine learning, the term inductive bias refers to a set of (explicit or implicit) assumptions made by a learning algorithm in order to perform induction, that is, to generalize a finite set of observation (training data) into a general model of the domain.
쉽게 말해 Training에서 보지 못한 데이터에 대해서도 적절한 귀납적 추론이 가능하도록 하기 위해 알고리즘(모델)이 가지고 있는 가정들의 집합이라는 것이다. 예를 들어 선형 회귀 모델을 사용한다는 것은 입력 데이터에 선형성이 존재한다는 것을 확인했거나, 혹은 선형성을 띈다고 가정해도 충분하다고 생각하기 때문이라고 할 수 있을 것인데, 이러한 것들이 Inductive Bias의 대표적인 예시가 된다.
Relational Inductive Biases on FCN & CNN & RNN
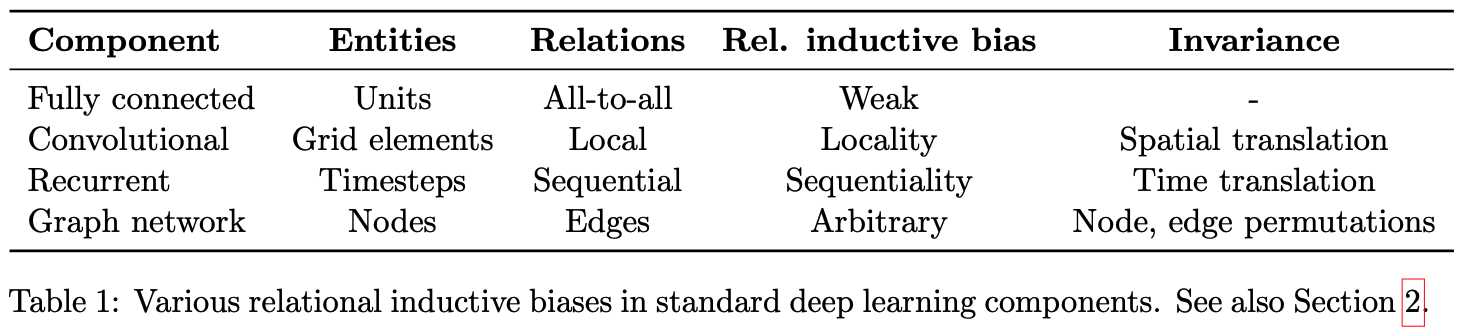
Inductive Bias는 크게 Relational Inductive Bias와 Non-relational Inductive Bias 두 개로 나뉜다. 이때 Relational Inductive Bias는 말 그대로 Inductive Bias 중에서도 어떤 관계에 초점을 맞춘 것이라고 할 수 있는데, 여기서 말하는 관계란 입력 Element와 출력 Element 간의 관계를 말한다.
Fully Connected
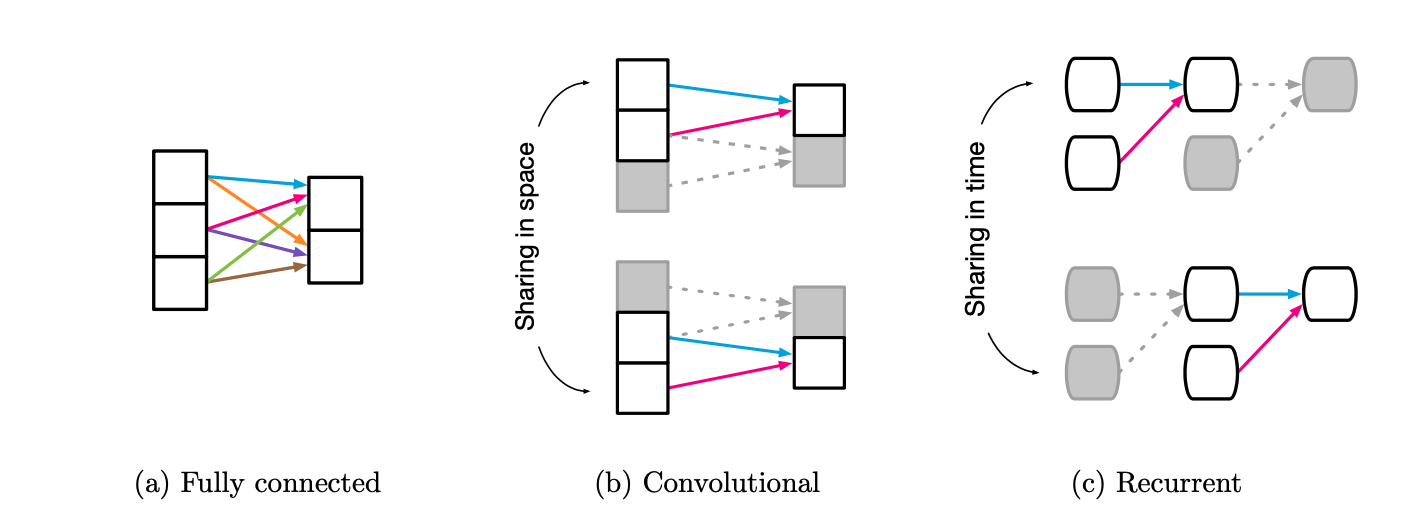
FCN부터 확인해보면, FCN의 입력 Entities가 개별 Unit으로 정의되며, 이들은 서로 모두 연결되어 있는 것으로 가정한다(All-to-all Relations). 모든 입력 Element가 모든 출력 Element에 영향을 미친다는 점에서 구조적으로 특별한 Relational Inductive Bias를 가정하지 않는다(Weak).
- Entities: Element
- Relation: All to All
- Rule: Weight & Bias
- Relational Inductive Bias: Weak(Nothing Special)
Convolutional
반면 CNN은 입력이 이미지처럼 격자(Grid) 구조로 되어 있다. 일반적으로 입력의 크기보다 작은 Convolution Filter를 사용하여 전체의 일부만을 대상으로 Convolution Operation을 수행하는데, 이때 하나의 Convolution Filter를 가지고 전체 격자를 순회하게 된다(Parameter Sharing). 이러한 점에서 CNN에서는 Entities 간의 Relation이 지역성, 즉 서로 가까운(Proximity) Element 간에만 존재한다고 가정하는 것으로 볼 수 있으며, 결과적으로 어떤 특성을 가지는 Element들이 서로 뭉쳐있는지 중요한 경우에 탁월한 구조가 된다. 또한 Parameter Sharing이라는 특성에 따라 Spatial Translation에 강력하다(Robust)는 특성을 가지고 있다.
- Entities: Element of Grid
- Relation: Local
- Rule: Convolution Filter(reuse)
- Relational Inductive Bias: Locality & Transitional Invariance
Recurrent
RNN 또한 CNN의 그것과 매우 유사한데, 공간의 개념을 시간의 개념으로 바꾼 것이라고도 볼 수 있다. RNN은 기본적으로 입력 값들이 시계열의 특성을 가지는 것으로 가정하며, 동일한 순서로 동일한 입력이 들어오면 출력이 동일하다는 점에서 Temporal Invariance의 특성을 가진다.
- Entities: Timesteps(Input & Hidden states)
- Relation: Sequential(Markov Dependency)
- Rule: Combine Input & Hidden and Return Next Hidden(reuse)
- Relational Inductive Bias: Sequentiality & Temporal Invariance
Relational Inductive Biases for Graph
Graph는 Node와 각 Node 간의 연결을 의미하는 Edge로 구성되는 자료구조를 말한다. Graph의 주된 특성은 크게 두 가지로 나누어 볼 수 있는데 하나는 Node 간의 관계를 나타내는 Edge가 임의로 존재한다는 것이고, 다른 하나는 Node와 Edge에 순서(order)가 없다는 것이다. 따라서 Graph를 잘 다루는 구조를 만들기 위해서는 이러한 두 가지 특성이 잘 반영될 수 있도록 해야 하는데, 구체적으로 입력 순서가 달라진다 할지라도 동일한 Graph라면 동일한 출력을 내보내야 한다.
- Entities: Nodes(No order)
- Relation: Edges
- Relational Inductive Bias: Permutational Invariance
생각해보면 현실의 많은 문제들이 입력의 순서와 무관한데, Graph를 잘 처리하는 구조가 중요한 이유가 여기에 있다. 이와 관련하여 논문에서는 태양계의 중심점을 구하는 문제를 예시로 들고 있다. 예를 들어 중심점을 구하고자 하는 태양계에 \(n\)개의 행성이 있다면 이에 대한 정보를 순서를 바꾸어가며 입력으로 전달하는 방법은 총 \(n!\)개가 있다. 결과적으로는 동일한 문제인데도 Permutation에 따라 문제가 매우 복잡해지는 것이다. 이때 Permutational Invariance한 구조를 사용하면 이를 보다 쉽게 해결할 수 있을 것으로 기대할 수 있다.
Graph Networks
논문에서는 Graph의 특성을 고려하여 기존에 제시된 방법론들을 확장하여 만든 Graph Netoworks(GN) Framework을 제시하고 있다. GN Block은 기본적으로 Graph를 입력으로 받아 Graph를 출력하는 Graph to Graph 구조(CNN은 Grid to Grid, RNN은 Seq to Seq로 볼 수 있다)이며, Graph의 정의에 따라 세 가지 구성요소, Entities가 되는 Node \(V\), 이들 간의 Relations이 되는 Edge \(E\), 그리고 전체 Graph의 특성을 표현하는 Global \(u\)를 처리하게 된다. 알고리즘은 다음과 같다.

가장 먼저 보이는 것은 Graph \((E, V, u)\)를 입력으로 받아 새로운 Graph \((E', V', u')\)를 반환한다는 것이다. 알고리즘은 크게 세 부분으로 구성되는데 Edge Feature, Node Feature, Global Feature를 차례대로 새로 구하게 된다. 그 과정에서 세 가지 Update Function \(\phi^e, \phi^v, \phi^u\)과 세 가지 Aggregation Function \(\rho^{e \rightarrow v}, \rho^{e \rightarrow u}, \rho^{v \rightarrow u}\)을 사용한다.
Update Function은 각각 새로운 Node, Edge, Global Feature를 구하는 함수라고 할 수 있으며, Neural Net(FCN, CNN, RNN 등) 뿐만 아니라 다양한 함수로 구현할 수 있다. Aggregation Function은 Elementwise Summation, Mean, Maximum 등과 같이 입력의 순서에 따라 출력이 영향을 받지 않는 함수, 즉 Permutational Invariance한 특성을 가진 함수로 구현되어야만 한다.
Design Principles of GN blocks
GN Block은 기본적으로 Graph를 다루는 문제들에 일반적으로 적용 가능한 Framework를 지향하며, 이를 위해 다음과 같은 요소들을 고려했다고 한다.
Flexible Representations
입력 값과 출력 값은 모두 Graph라고 하더라도 Graph를 구성하는 구성 요소들 \(E, V, u\)는 다양한 형태가 가능해야 한다. 또한 다양한 Graph 구조를 모두 다룰 수 있어야 한다.
Configurable within-block structure
다양한 형태로 Graph의 입력과 출력이 주어질 수 있는 만큼 Block의 내부 구조도 그에 맞춰 구성할 수 있어야 한다. 이미지가 주어진다면 Update Function으로 CNN을, Sequence가 주어지면 RNN을 사용할 수 있어야 한다. 또한 문제의 특성에 맞춰 출력 값을 구성할 수 있어야 한다. 이와 관련하여 논문에서는 다음 6가지의 내부 구조를 제시한다. 위에서 확인한 알고리즘은 \((a)\)이며, 필요에 따라 일부만 사용하는 식으로 내부 구조를 달리하고 있다.
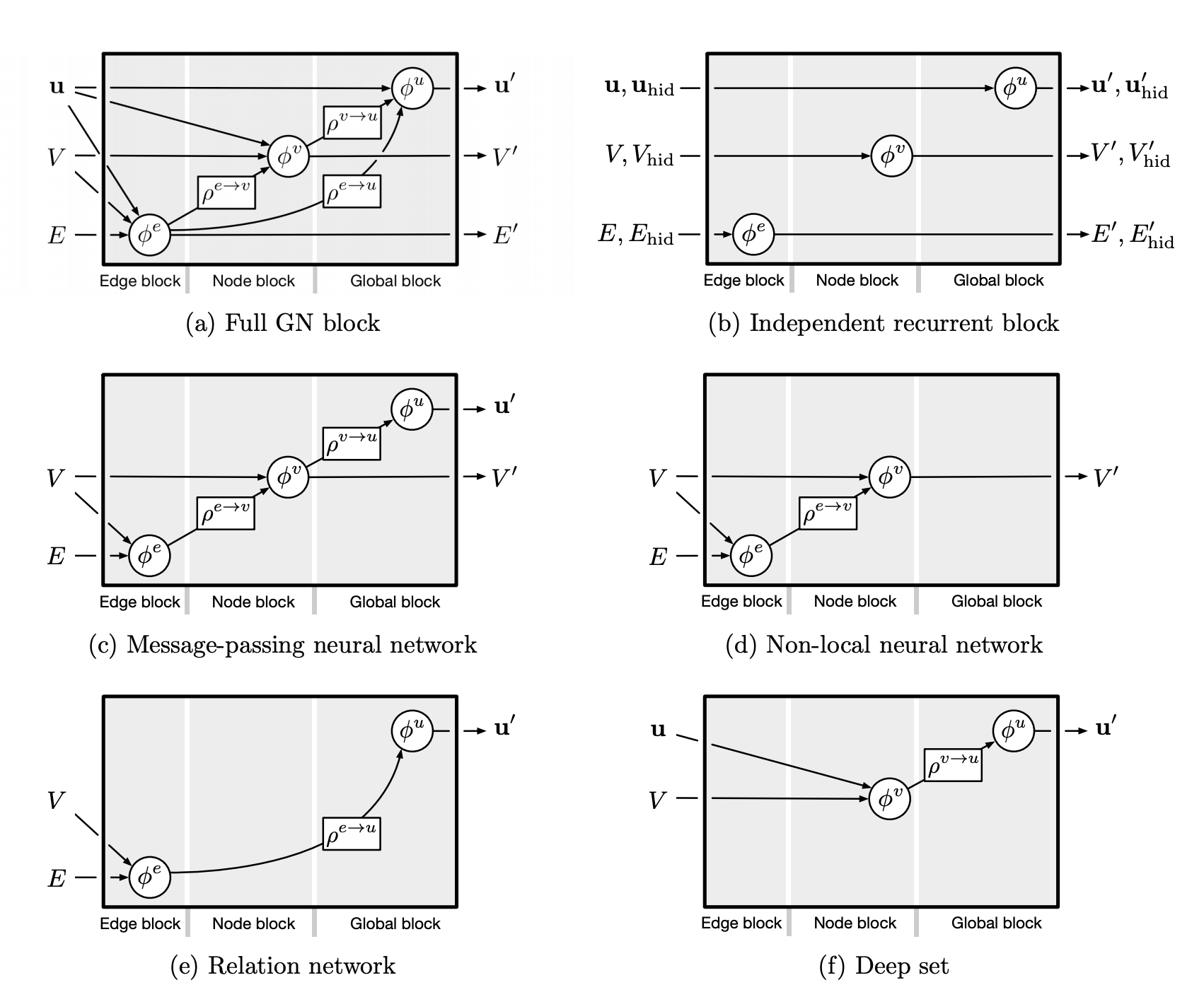
Composable multi-block architectures
\(\text{GN} (\text{GN} (graph))\)와 같이 GN Block을 다양한 형태로 조합할 수 있어야 한다.