논문 제목 : Semi-Supervised Classification with Graph Convolutional Networks
- Thomas N. Kipf, Max Welling
- 2017
- Paper Link
Summary
- 일반적인 형태의 Graph에 대해 곧바로 Convolution 연산을 수행하는 것은 어려움이 많다.
- GCN에서는 Spectral Convolution를 적용하여 Graph에 대해서도 적용이 가능한 효율적인 Convolution 연산 방법을 제시한다.
- 이를 통해 논문에서는 Node를 분류하는 문제를 해결하고 있지만 Graph를 입력으로 받는 다양한 문제에 대해서도 적용이 가능하다.
Introduction
Graph Convolution Network(GCN)이란 이미지에 많이 사용되는 Convolution 연산을 Graph의 특징을 추출하는 데에 사용하는 방법이라고 할 수 있다. 이미지라는 것은 격자(Grip)의 Node들이 서로 일정하게 연결되어 있는 Graph의 특수한 형태로 볼 수 있는데, 이를 격자 구조가 아닌 일반적인 Graph에서도 사용할 수 있도록 하겠다는 것이다.
물론 이를 곧바로 적용하기에는 몇 가지 문제들이 존재한다. 개별 Node마다 인접 Node의 개수가 다른 상황을 어떻게 처리할 것인지에 대한 문제가 대표적이다. 즉 이미지와 같은 격자 구조에서는 주변부에 있는 Node를 제외한 나머지 Node들은 모두 상하좌우 및 대각의 총 8개의 이웃 Node를 가지며, 각각의 이웃 Node의 위치를 현재 Node를 기준으로 규정할 수 있다. 하지만 일반적인 Graph는 개별 Node가 가지는 이웃 Node의 개수가 모두 다를 뿐 아니라 각 이웃 Node 간의 순서를 규정할 만한 방법이 쉽게 떠오르지 않는다.
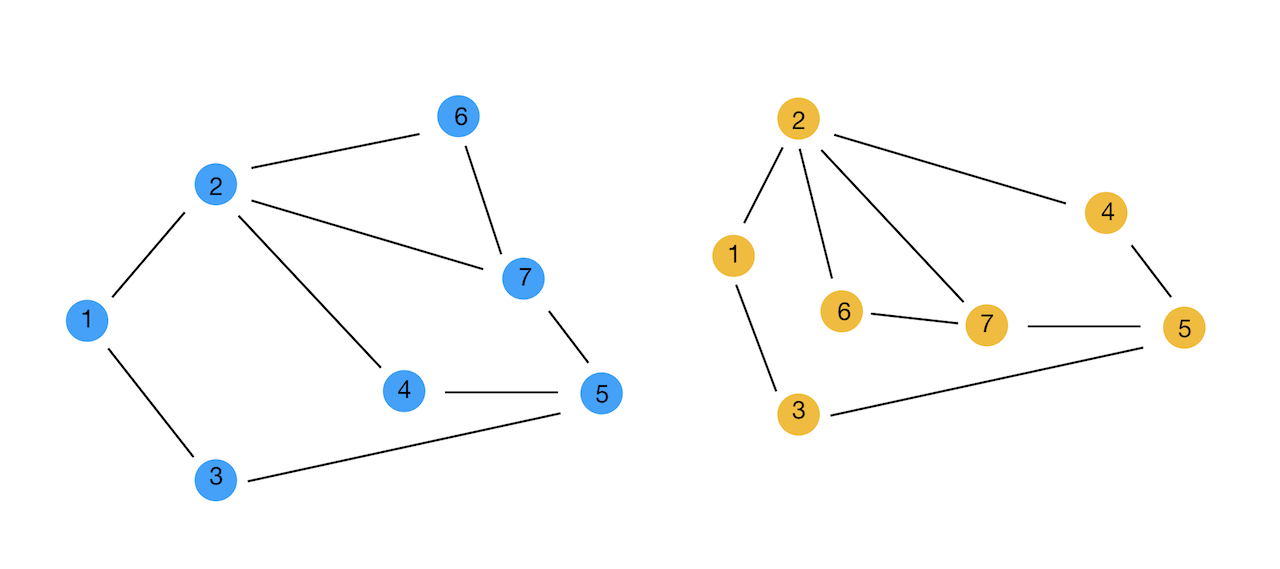
위의 두 그래프는 Node의 개수와 연결된 Edge가 동일한, 즉 동일한 Graph이지만 표현 방법에 따라 Node의 위치가 다르다. 따라서 Node와 Node 간의 관계를 위치로 규정하기 어렵다. 또한 1번 Node의 이웃 Node의 개수는 2개, 2번 Node의 이웃 Node의 개수는 4개와 같이 각 Node의 이웃 Node의 개수가 다르다. Graph의 이러한 특성은 아래와 같은 Convolution Filter를 어떻게 적용할 지에 대한 문제로 이어지게 된다.
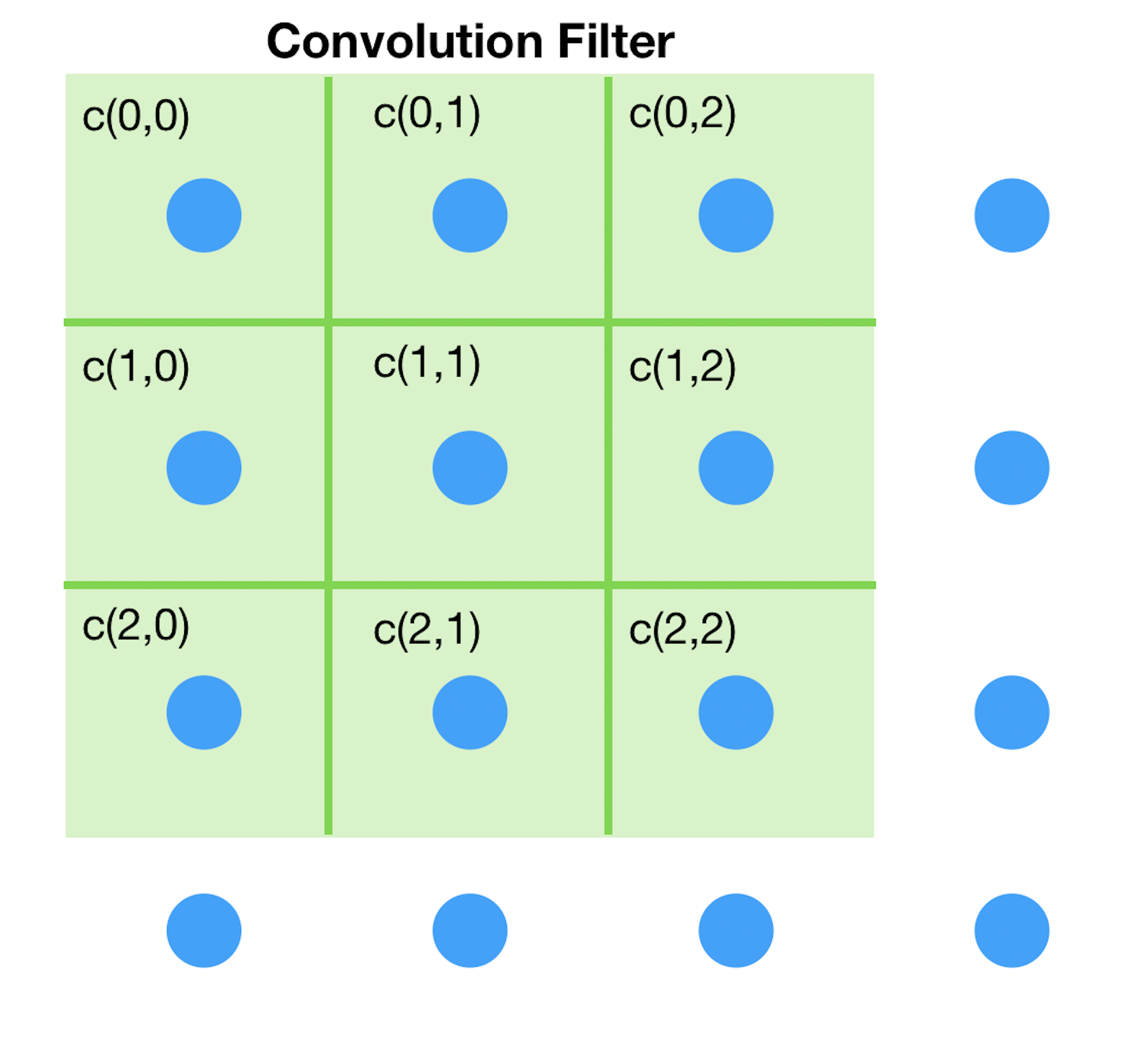
Graph Convolution Network는 Spectral Convolution을 통해 이러한 문제를 극복하고 Graph에 Convolution을 적용하는 방법을 제시한다.
Spectral Convolution
Spectral Graph Theory란 Adjacency Matrix, Laplacian Matrix 등과 같이 Graph와 관련된 행렬을 사용한 특성 다항식 및 고유 값 및 고유 벡터를 통해 그래프의 특성을 분석하는 방법에 관한 학문이라고 한다. Spectral Convolution이란 Spectral Graph Theory에 기반하고 있으며 다음과 같이 정의된다.
\[g_\theta \star x = Ug_\theta U^Tx\]여기서 \(g_\theta\)는 Convolution Filter를, \(U\)는 Laplacian Matrix \(L\)의 EigenVector를 의미한다. Convolution을 위의 식과 같이 표현할 수 있다는 것을 확인하기 위해서는 Laplacian Matrix와 Convolution Theorem에 대해 알아야 한다.
Laplacian Matrix
먼저 일반적으로 말하는 Laplacian Matrix \(L\)이란 다음과 같이 Degree Matrix에 Adjecency Matrux를 뺀 것이다. 참고로 Degree Matrix는 \(D_{ii} = \Sigma_j A_{ij}\), 즉 Node \(i\)의 이웃 Node 갯수를 Diagonal Element로 갖는 Diagonal Matrix를 말한다.
\[L = D - A\]논문에서 사용하고 있는 Laplacian Matrix는 Normalized Laplacian Matrix이다.
\[L = I_N - D^{-{1 \over 2}}AD^{-{1 \over 2}}\]위키에 따르면 Laplacian Matrix가 가지는 주요 특징으로 다음과 같은 것들이 있다고 한다.
- \(L\)은 대칭 행렬이다. 따라서 EigenVector \(\mu_l\)는 orthogonal한 특성을 가진다.
- \(L\)은 Positive-Semi Definitive(SVD에서 정리)한 속성을 가지고 있으며, 따라서 EigenValue \(\lambda\)가 항상 0보다 크거나 같다 : \(0 \leqq \lambda_0 \leqq \lambda_1 \leqq ... \leqq \lambda_{n-1}\)
Convolution Theorem & Graph Fourier Transform
Convolution Theorem은 다음과 같은 특성을 말한다.
\[f \star g(x) = F^{-1}(F(f) \cdot F(g))\]즉 \(f\)라는 시그널에 대해 \(g\)라는 Convolution Filter로 Convolution을 수행한다는 것은 각각에 대해 Fourier Transform \(F\)을 수행한 뒤 그것을 곱하고 다시 Inverse Fourier Transform \(F^{-1}\)을 해준 것과 동일하다는 것을 의미한다.
\[f \rightarrow \chi^T f \rightarrow \hat g(\lambda) \chi^T f \rightarrow \chi \hat g(\lambda) \chi^T f\]이와 관련해서 논문에서는 Graph에서의 Spectral Convolution을 다음과 같이 시그널 \(x \in R^N\)과 convolution filter \(g_\theta(\Lambda) = \text{diag}(\theta)\)간의 곱으로 표현하고 있다.
\[g_\theta \star x = U g_\theta U^T x\]이것이 어떻게 가능한가 하면, Graph Fourier Transform에서는 Fourier Tranform과 Inverse Fourier Transform을 다음과 같이 Laplacian의 EigenVector \(U\)로 구한하는 점을 참고할 수 있다.
- Fourier Tranform: \(F(x) = U^Tx\)
- Inverse Fourier Tranform: \(F^{-1}(x) = Ux\)
Chebyshev Spectral Convolution
하지만 위의 식을 곧바로 딥러닝에 적용하기에는 몇 가지 문제점이 있다. 첫 번째는 연산 비용 문제로 Graph의 크기가 크면 클수록 Laplacian Matrix를 Eigen Decomposition 비용이 늘어나게 되고, 이들 간의 곱을 수행하는 것 또한 큰 연산 비용을 요구한다. 그리고 딥러닝으로 모사할 대상이 무엇인지 애매하다는 점 또한 문제라고 할 수 있다. 이와 관련하여 Chebyshev Polynomial \(T_k(x)\)를 적용하여 다음과 같이 파라미터 \(\theta'\)를 Neural Net으로 모사해 학습하는 방법이 제시되었다.
\[g_{\theta'}(\Lambda) \approx \Sigma_{k=0}^{K} \theta'_k T_k(\tilde \Lambda)\]이때 \(K\) 값의 크기는 Chebyshev Polynomial \(T_k(x)\)를 몇 번 근사할 것인가를 의미하며, \(\theta'_k \in R^K\)는 Chebyshev 계수 벡터를 의미한다. Chebyshev Polynomial \(T_k(x)\)와 관련된 특성은 다음과 같다.
\[\eqalign{ &T_k(x) = 2xT_{k-1}(x) - T_{k-2}(x)\\ &T_0(x) = 1 \\ &T_1(x) = x \\ &\tilde \Lambda = {2 \over \lambda_{\text{max}}} \Lambda - I_N }\]정리하면 시그널 \(x\)에 대한 filter \(g_{\theta'}\)로의 Chebyshev Spectral Convolution은 다음과 같다.
\[g_{\theta'}\star x \approx \Sigma_{k=0}^{K} \theta'_k T_k(\tilde \Lambda)x\]Graph Convolution Neural Network
논문에서 제시하는 GCN은 Chebyshev Spectral Convolution을 근사하여 보다 쉽게 구하려는 시도라고 할 수 있다. 구체적으로는 다음과 같이 정리할 수 있다.
- \(K\)는 1로 하고 여러 개의 Layer를 쌓는다.
- \(\lambda_{\text{max}}\)를 2로 추정하고, Neural Net이 이에 맞춰 훈련되도록 한다.
위 두 조건을 적용하면 Chebyshev Spectral Convolution 식을 다음과 같이 정리할 수 있다.
\[\eqalign{ g_{\theta'}\star x &\approx \Sigma_{k=0}^{K} \theta'_k T_k(\tilde \Lambda)x\\ &=\theta'_0 T_0(\tilde L)x + \theta'_1 T_1(\tilde L)x \qquad ... \ (K=1)\\ &= \theta'_0 x + \theta'_1 \tilde L x \qquad \qquad ... \ (T_0=1, T_1 = x)\\ &= \theta'_0 x + \theta'_1({2 \over \lambda_{\text{max}}} \Lambda - I_N)x \\ &= \theta'_0 x + \theta'_1({2 \over 2} \Lambda - I_N)x \qquad ... (\lambda_{\text{max}} = 2)\\ &= \theta'_0 x + \theta'_1((I_N - D^{-{1 \over 2}}AD^{-{1 \over 2}}) - I_N)x \\ &= \theta'_0 x + \theta'_1(D^{-{1 \over 2}}AD^{-{1 \over 2}})x \\ }\]이렇게 되면 파라미터 \(\theta'\)가 \(\theta'_0\), \(\theta'_1\) 두 개가 된다. 오버피팅의 가능성을 낮추고 연산량을 줄이기 위해서는 레이어 당 파라미터의 숫자를 줄이는 것이 좋으므로 다음과 같이 하나의 \(\theta\)로 바꾸어 구성했다고 한다.
\[g_{\theta'}\star x \approx \theta (I_N + D^{-{1 \over 2}}AD^{-{1 \over 2}})x \qquad ... (\theta = \theta'_0 = -\theta'_1)\]이렇게 했을 때 \(I_N + D^{-{1 \over 2}}AD^{-{1 \over 2}}\)는 \([0,2]\)의 범위를 가지는 EigenValue들을 가지게 된다고 한다. 그런데 이와 같은 연산을 반복적으로 여러 레이어에 거쳐 수행하면 불안정할 수 있고, Gradient Vanishing 문제에도 취약할 수 있다고 한다. 이러한 가능성을 줄이고 안정적인 학습을 위해 한 번 더 Normalize 해주는 Normalization Trick을 도입하고 있다.
\[\eqalign{ &I_N + D^{-{1 \over 2}}AD^{-{1 \over 2}} \rightarrow \tilde D^{-{1 \over 2}}\tilde A \tilde D^{-{1 \over 2}}\\ &\text{where } \tilde A = A + I_N, \tilde D_{ii} = \Sigma_j \tilde A_{ij} }\]마지막으로 \(N\)개의 Node가 각각 \(C\)차원의 feature vector를 표현하는 시그널 \(X \in R^{N \times C}\)에 대해 다음과 같이 일반화하여 표현할 수 있다.
\[Z = \tilde D^{-{1 \over 2}} \tilde A \tilde D^{-{1 \over 2}} X \Theta\]\(\Theta \in R^{C \times F}\)는 matrix of filter parameter이고 \(Z \in R^{N \times F}\)는 Convolution을 수행한 결과로, 각 Row는 각 Node의 특성을 반영하게 된다. 논문과 같이 Node를 분류하는 문제라면 이 \(Z\)값의 각 Row Vector를 분류하는 것이 된다.
2-layer GCN
위의 식을 바탕으로 논문에서는 2-layer GCN 식을 다음과 같이 제시한다. 이를 통해 각 Node를 속성에 맞게 분류할 수 있다고 한다.
\[Z = f(X, A) = \text{softmax} (\hat A \text{ReLU} (\hat A X W_0) W_1)\]여기서 \(\hat A\)은 \(\tilde D^{-{1 \over 2}} \tilde A \tilde D^{-{1 \over 2}}\)를 뜻하며 전체 Graph의 Network 특징을 담고 있는 feature로 볼 수 있다. 입력은 각 Node의 Feature Matrix인 \(X \in R^{N \times C}\)이고, 두 개의 Weight 값 \(W_0, W_1\) 중 \(W_0 \in R^{C \times H}\)은 입력을 Hidden Vector로 보내는 Weight라고 할 수 있다. 그리고 \(W_1\)가 Hidden Vector를 받아서 Output Vector로 바꾸어준다.
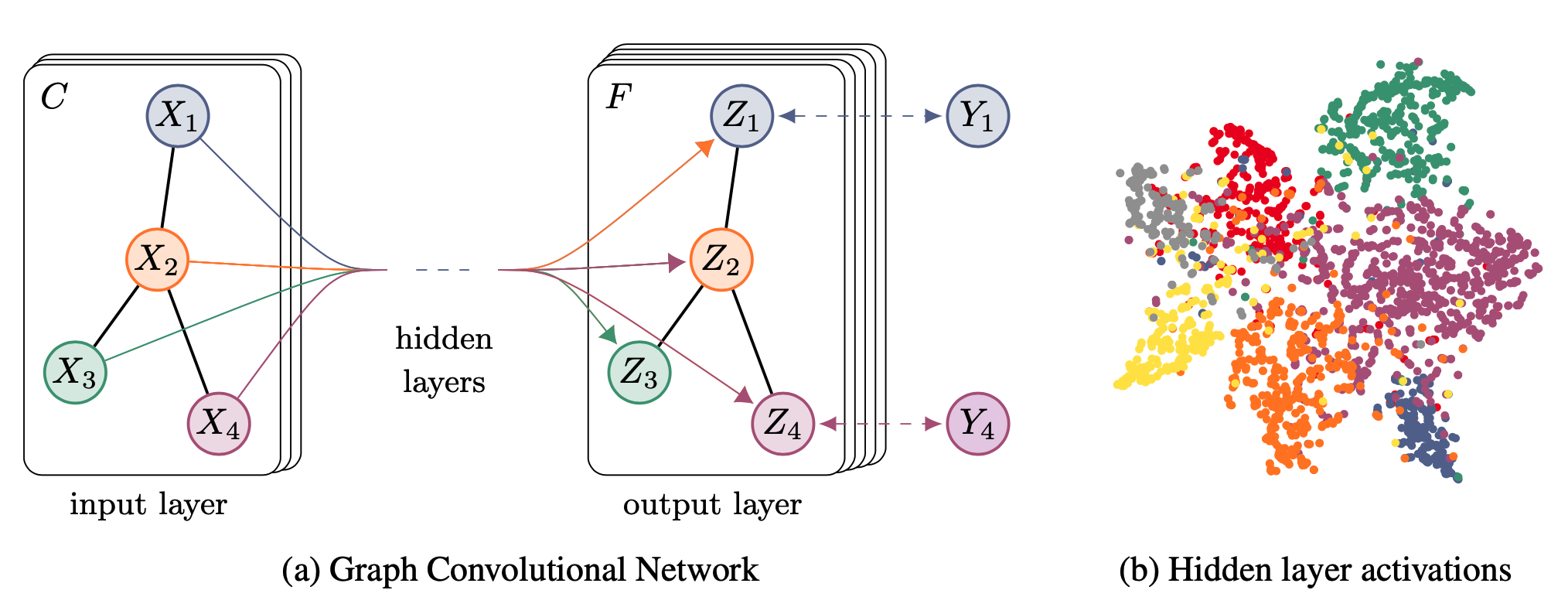
논문에서 풀고자 하는 문제는 Semi Supervised classification 이므로 레이블이 몇몇 Node에 대해서만 존재하는 상황이다. 이를 표현하는 것이 위의 그림에서 \(Y_1, Y_4\)로, 2, 3 Node에 대해서는 레이블이 없고 1, 4 Node에 대해서만 Loss를 구하고 학습을 진행하게 된다.