논문 제목 : Large-Scale Learnable Graph Convolutional Networks
- Hongyang Gao, Zhengyang Wang, Shuiwang Ji
- 2018
- Paper Link
Summary
- 기존 방법인 GCN은 Graph의 크기에 따라 연산량이 매우 크게 증가하고, layer를 많이 쌓지 못한다는 문제를 가지고 있다.
- LGCN은 GCN과 달리 특수한 Convolution을 사용하지 않고, Graph를 Grid-like 형태로 바꾸어 일반적인 Convolution을 적용할 수 있는 방법을 사용한다.
- layer를 많이 쌓을 수 있도록 skip connection을 추가했으며 Graph의 복잡도에 따라 layer의 갯수와 \(k\)의 크기를 늘리는 방식으로 대응할 수 있다고 한다.
Introduction
Graph와 관련하여 대표적인 문제는 Graph를 구성하는 Node들을 분류하는 것이다. 이를 위해서는 개별 Node의 특징을 추출해야 하는데 관련하여 GCN(Graph Convolution Network) 등과 같이 이미지에서 많이 사용되는 Convolution Operation을 적용하는 방법론이 발전해왔다. 하지만 Convolition Operation은 이미지처럼 Grid-Like 데이터에 사용되는 방법으로 이를 Graph에 적용하는 것은 다음 두 가지 근본적인 문제를 가지고 있다.
- Node 마다 인접 Node의 숫자가 다르다(difference of number of neibhoring nodes).
- 인접 Node를 줄세울 방법이 없다(no ranking information).
Grid-Like Graph는 위의 두 가지 특징을 모두 만족하는 특별한 Graph라고 한다면 일반적인 Graph에 Convolution Operation을 적용하기 위해서는 특수한 방법론들이 필요하다고 할 수 있다.
The Pioneer: Graph Convolution Network
GCN은 이러한 문제를 Spectral Graph Convolution이라는 Spectral Graph Theroy의 방법론을 적용하여 해결한다. 쉽게 말해 Convolution의 방식을 변경하는 것이다. 따라서 GCN은 결과적으로 Convolution Operation의 기본적인 아이디어, 즉 이웃 Node의 Feature를 반영하여 각 Node의 Feautre를 업데이트하는 방식을 따르기는 하지만 일반적인 CNN과는 다른 방식으로 구현된다. 다음은 GCN을 구성하는 한 layer에 대한 수식으로, \(X_l\)을 입력으로 받아 \(X_{l+1}\)을 출력하게 된다. 이와 관련하여 자세한 내용은 다음 포스팅에서 다루고 있다.
\[X_{l+1} = \sigma ( \tilde D^{-{1 \over 2}} \tilde A \tilde D^{-{1 \over 2}} X_l W_l )\]이러한 특별한 Convolution을 도입하여 GCN은 Node에 따라서 reception field의 갯수가 다르면서도 하나의 Node Feature를 업데이트할 때 이웃 Node에 적용되는 weigth 값의 총합은 같도록 할 수 있다는 점에서 유용한 방법론이다. 하지만 GCN은 다음과 같은 단점을 가지고 있다.
- 전체 Adjecency Matrix를 가지고 직접적인 연산을 수행하므로 Matrix의 크기에 따라 비용이 크게 증가한다.
- 2-layer를 주로 사용한다. 즉 layer의 깊이가 깊어질수록 성능이 떨어진다는 문제가 있다.
당연하게도 논문에서 제시하는 LGCN(Large-Scale Learnable Graph Convolutional Networks)은 이러한 문제를 해결하려고 한다.
Learnable Graph Convolutional Layer
LGCN(Learnable Graph Convolutional Network)의 가징 큰 특징은 Graph data를 Grid-Like한 형태로 바꾸어 Convolution Operation을 적용하는 것이라고 할 수 있다. 이를 위해서는 Graph와 Grid-Like의 두 가지 차이점, (1) 각 Node의 이웃 Node의 개수가 다르다는 것과 (2) 이웃 노드들을 줄세울 수 없다는 점을 해결해야 하는데, 그 과정은 다음 두 가지 단계로 나누어 진행된다. 논문에 나오는 아래 그림을 참고하면 보다 쉽게 이해할 수 있다.
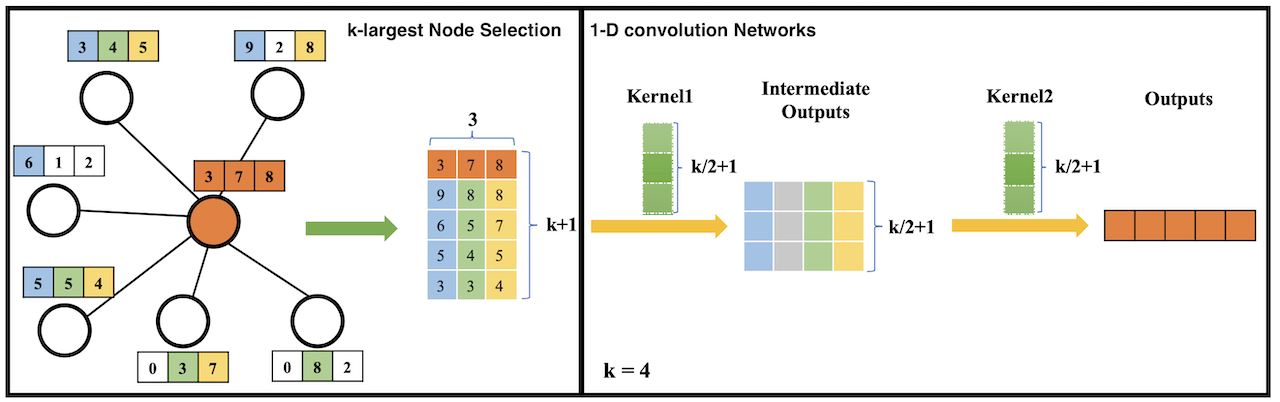
(1) \(k\)-largest Node Selection
각 layer \(l\)의 \(k\)-largest Node Selection은 다음 수식과 같이 표현할 수 있다.
\[\tilde X_l = g(X_l, A, k)\]여기서 \(X_l\)은 layer의 입력을, \(A\)는 Adjecency Matrix를 의미한다. \(k\)는 하이퍼파라미터로 사용할 Feautre의 갯수라고 할 수 있다. \(g(\cdot)\)은 다음과 같은 과정으로 이뤄진다.
- \(X_l \in R^{N \times C}\)로, 각각의 row \(x_l^i\)는 \(i\)번째 Node의 특징을 나타낸다. 이들 중 Node \(i\)와 이웃하는 Matrix를 Adjecency Matrix \(A\)를 통해 확인하여 골라낸다.
- 이렇게 구해진 Node \(i\)의 이웃 Node들의 Feature \(\{ x_l^{i1} ... x_l^{in} \}\)을 Concat한다. 이렇게 만들어진 Matrix를 \(M_l^i\)라고 한다. 이때 \(N < k\)인 경우에는 0 padding을 추가하여 \(N \times C\)에 맞추어 준다.
- \(M_l^i\)에 대해 \(k\)-largest node selection을 수행하게 된다. 여기서 중요한 것은 node selection이라 하여 개별 node의 feature를 유지하며 sorting하는 것이 아니라는 점이다. 즉 어떤 node의 feature인지와 무관하게 \(M_l^i\)의 column 별로 오름차순으로 정렬한다.
- \(M_l^i\)에서 \(K+1\)번 row 부터는 모두 버린다. 그리고 첫 번째 row로 \(X_l^i\), 즉 자기 자신 Node를 Concat하여 붙인다.
- 모든 Node에 대해 똑같이 수행한다. 최종적으로 \(\tilde X_l\)은 \(R^{N \times (k+1)\times C }\)의 크기를 가지게 된다. 이를 \(g(\cdot)\)의 출력값 \(\tilde X_l\)이라고 한다.
(2) 1-D Convolution Networks
다음으로는 1-D Convolution Operation을 적용하게 된다. 수식은 다음과 같다.
\[X_{l+1} = c(\tilde X_l)\]참고로 \(\tilde X_l\)는 \(N \times (k+1)\times C\) 형태로 주어지는데, 1-D Matrix로 보게되면 각각은 다음을 의미한다.
- \(N\): batch size
- \(k+1\): spatial size
- \(C\): Number of Channels
따라서 1-D Convolution의 결과는 \((N \times 1 \times D)\)가 되어야 한다. 여기서 \(D\)는 Updated Feature Space, 즉 출력의 Feature 크기라고 할 수 있다. 1-D Convolution을 수행하는 횟수는 하이퍼파라미터이고 최종적으로 각 Node의 Feature가 \((1 \times D)\)로만 나오면 된다고 한다.
Learnable Graph Convolutional Network

LGCL은 하나의 Layer에 관한 내용으로, 이를 사용하여 전체 모델 LGCN은 다음과 같이 구성할 수 있다.
- Graph Embedding Layer로 Graph의 Node Feature 차원의 크기를 줄일 수 있도록 한다: \(X_1 = X_0 W_0\)
- Graph의 복잡도에 비례하여 LGCL을 쌓는다.
- 각 LGCL layer마다 Skip-Connections를 적용하여, layer의 출력을 입력과 Concat하여 전달한다.
- 마지막 Layer의 출력을 Fully-Connect에 연결하고 Softmax를 적용하여 분류문제에 사용한다.
Model에 있어 LGCL의 갯수와 \(k\)의 크기가 주된 하이퍼파라미터로, 문제의 복잡성이 높을수록 크게 가져가는 것이 좋다고 한다.
Sub-Graph Training on Large-Scale Data
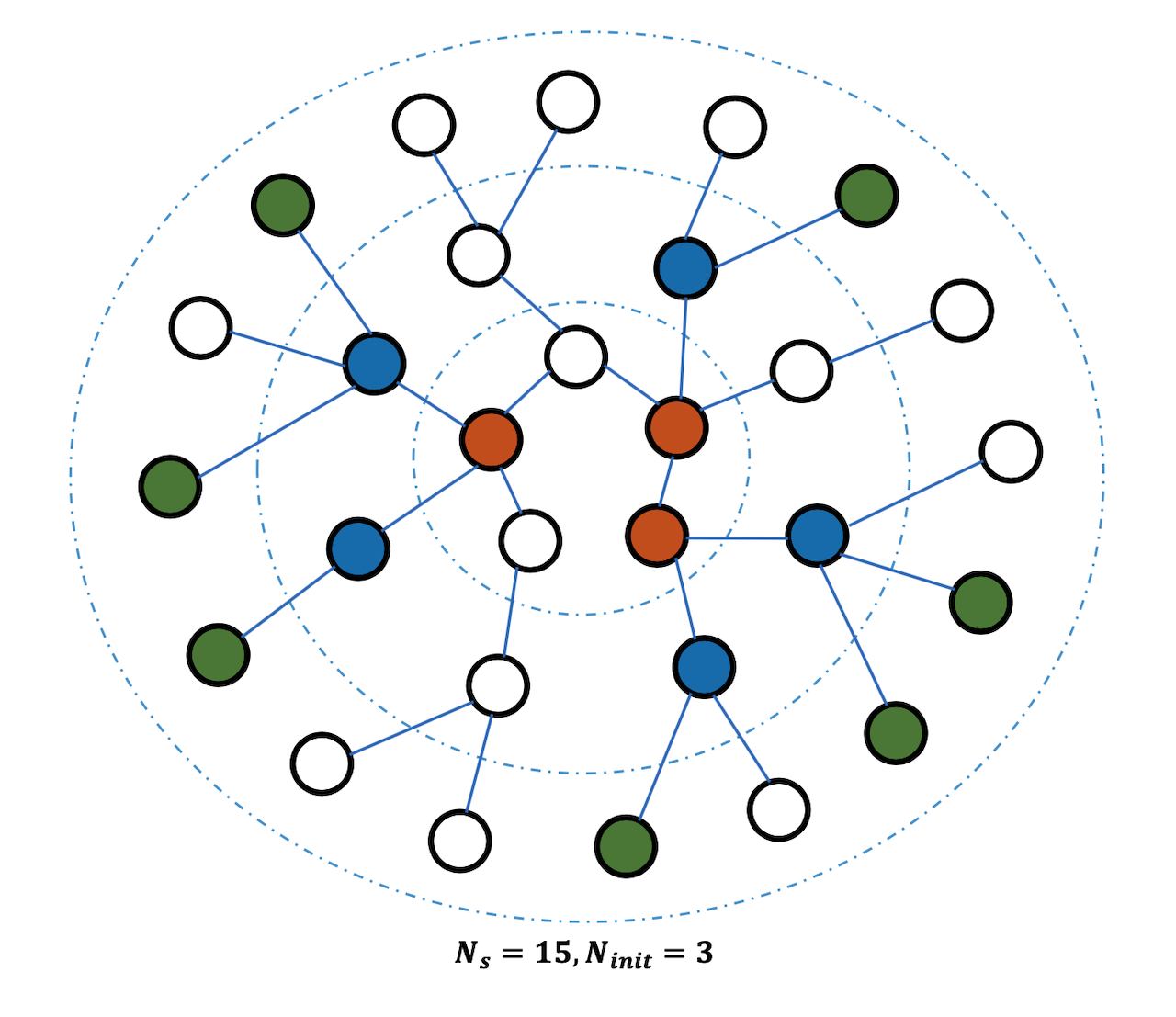
LGCN은 GCN 등에 비해 연산량은 줄였지만, 곧바로 전체 Graph에 대해 적용하게 되면 이 또한 Memory를 비롯하여 비용이 커질 수 밖에 없다는 문제가 있다. 이러한 문제를 해결하기 위해 논문에서는 전체 Graph의 일부(Sub-Graph)에 대해서 훈련하는 방식을 제시한다.

Sub-Graph는 전체 Graph를 임의로 crop하여 구성하게 된다. 그런데 임의로 Node를 선택하는 것이므로 각 Node의 모든 이웃 Node가 Sub-Graph에 포함되지 않을 수도 있다. 이 경우 이웃 Node를 결정할 때 BFS 알고리즘을 사용하여 Sub-Node에 포함된 Node만으로 학습이 이뤄질 수 있도록 한다.