논문 제목 : GAN) Generative Adversarial Nets
- Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio
- 2014
- 논문 링크
- 튜토리얼 링크
Summary
- Adversarial Training이란 Generator와 Discriminator라는 두 모델이 서로 경쟁하며 발전하는 방식이다.
- Discriminator는 실제 데이터인지, 생성된 데이터인지 구별하는 역할을 하고 Generator는 실제 데이터와 유사한 데이터를 만들어 Discriminator를 속이는 것을 목표로 한다.
- Generator, Discriminator 모두 완벽히 학습되면 Discriminator는 \(1/2\)를 출력하며 실제 데이터와 생성 모델의 데이터를 구별하지 못하게 되는 것이 수학적으로 증명되어 있다.
Generative Models
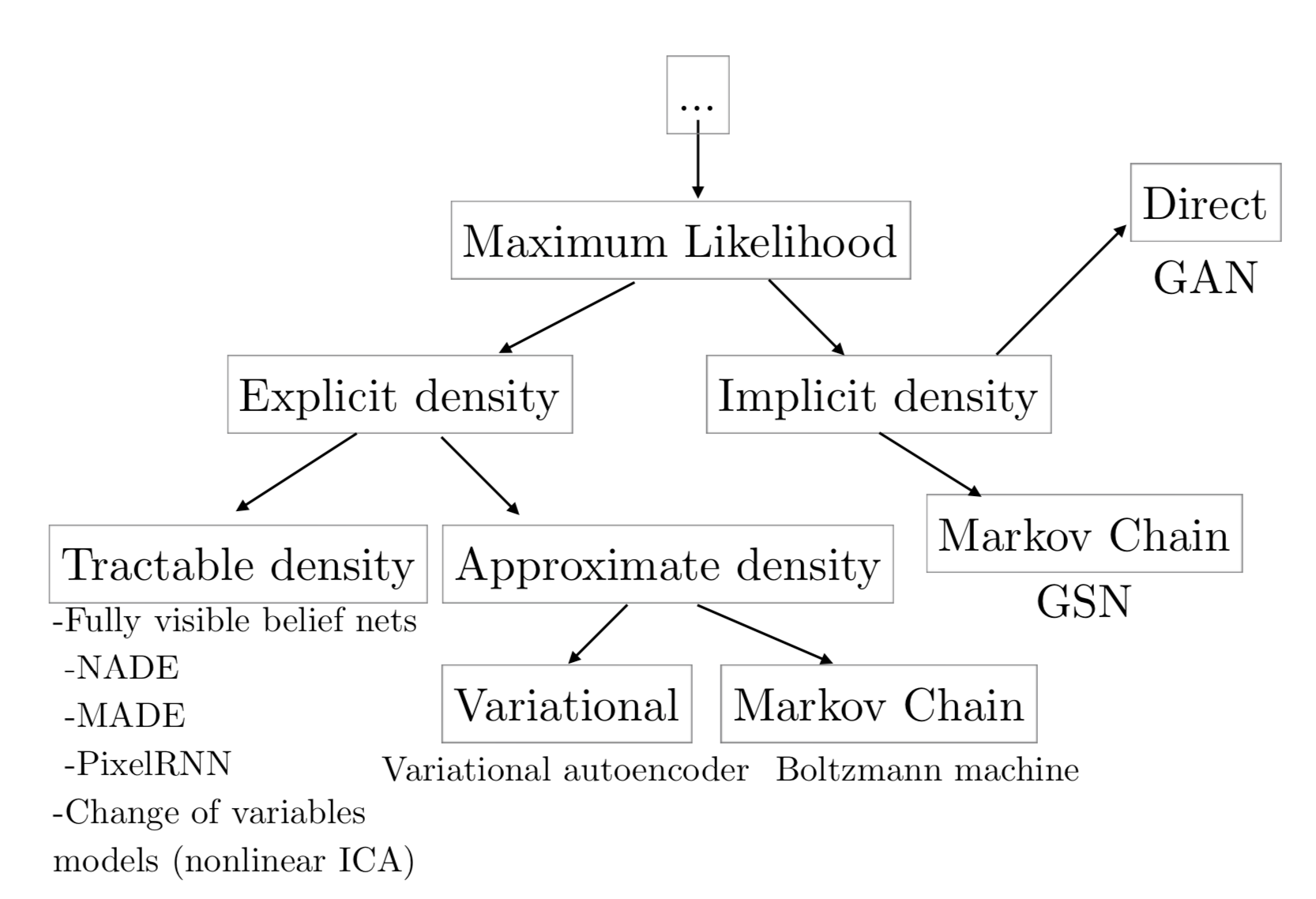
생성 모델이란 주어진 데이터의 분포를 학습하여 그와 유사한 데이터를 생성해내는 모델이라고 할 수 있다. GAN은 Generative Model의 대표적인 예시 중 하나로서 주관적으로 볼 때 이미지 등을 가장 잘 생성해내는 모델로 유명하다. 2016년 NIPS Tutorial: Generative Adversarial Networks에서 GAN의 저자 Ian Goodfellow는 Maximum Likelkihood Estimation을 사용하는 생성 모델을 다음과 같이 분류하고 있다.
Generative Model with MLE
Maximum Likelihood Estimation(MLE)는 말 그대로 Likelihood를 극대화하는 방향으로 모델을 업데이트하는 것을 말한다. 즉 training set \(X\)의 데이터 \(x_1, x_2, ... x_n\)에 있어 \(\Pi_{i=1}^n p_{model} (x_i; \theta)\)를 극대화하는 parameter \(\theta\)를 찾는 것이라고 할 수 있다.
\[\theta^* = \arg \max_\theta \Pi_{i=1}^n p_{model} (x_i; \theta)\]이때 일반적으로 \(\log\)를 붙여 곱이 아닌 덧셈으로 표현한다. \(\log\)는 단조 증가 함수이므로 가능하다.
\[\theta^* = \arg \max_\theta \Sigma_{i=1}^n \log p_{model} (x_i; \theta)\]한 가지 더 알아두어야 하는 것은 MLE는 data의 분포 \(p_{data}\)와 \(p_{model}\)간의 KL Divergence를 줄이는 것과 완벽하게 일치한다는 점이다.
\[\theta^* = \arg \min_\theta KL(p_{data(x)} \| p_{model}(x;\theta) )\]Classification of Generative Model
MLE를 사용하는 생성 모델을 Ian Goodfellow는 크게 두 갈래, Explicit Density Method와 Implicit Density Method 두 가지로 나누어 보고 있다. Explicit Density Method는 \(P_{model}(x;\theta)\)를 직접 정의하는 방법을 말한다. 이러한 방법은 다시 정확히 계산 가능한 확률 분포(Tractable)를 가정하는지 그렇지 않은 확률 분포(Intractable)를 가정하는지로 나뉘는데, Tractable Explicit Density Model로는 FVBN(1998), Intractable Explicit Density Model로는 Variational Inference를 사용하는 VAE(2013)와 Markov chain을 사용하는 Boltzmann machine이 있다.
참고로 VAE는 Intractable하다는 문제점을 Approximation으로 해결한다. VAE 알고리즘에서 직접 함수를 구하는 것이 아닌 비교적 구하기 쉬운 Lower Bound를 극대화하는 방향으로 학습을 진행하는 것을 이러한 관점으로 이해할 수 있다.
GAN은 기본적으로 \(P_{model}(x;\theta)\)를 정확히 정의하지 않는 Implicit Density Model이다. Implicit Density Model은 간접적으로, 즉 sampling을 통해서 \(P_{model}\)에 대해 학습하게 된다. 기존의 방법 중 대표적인 것으로 Markov Chain을 사용하는 Generative Stochastic Network(2014)가 있다. Ian Goodfellow는 그림에서도 확인할 수 있듯이 GAN은 mplicit Density Model이지만 기존의 방법과는 전혀 다른 방식으로 동작한다는 것을 강조한다. 그러면서 기존의 방법들과 비교하며 GAN이 아래와 같은 장점을 가지고 있다고 주장한다.
- Markov Chain은 image와 같이 모델링하고자 하는 대상이 커지면 적용하기 어렵고, multi step sampling을 수행하기 때문에 상대적으로 비용이 많이 든다는 점이 문제라고 지적하며 GAN 또한 Sampling을 기반으로 하지만 기본적으로 single step sampling이라는 점에서 자유롭다고 한다.
- VAE의 경우 universal approximate 하다는 것이 증명되지 않았으나 GAN Framework는 universal approximator로 알려져 있다.
- 주관적으로 볼 때 GAN의 결과물이 다른 방법을 사용하는 것보다 더 좋다.
Adversarial Training
GAN의 가장 핵심적인 아이디어는 Adversarial Training이다. Adversarial이라는 표현에서도 알 수 있듯이 GAN은 두 개의 모델을 동시에 학습시키며 두 모델이 서로 경쟁하면서 발전하게 된다. 이때 두 개의 모델, Generator \(G\)와 Discriminator \(D\)의 목표는 아래와 같다.
Generative 모델의 목표
- 실제 데이터의 분포를 학습하여 그와 유사한 새로운 데이터를 생성해내는 것
- Discriminator가 실제 데이터와 구별하지 못하는 데이터를 생성해내는 것
Discriminator 모델의 목표
- 실제 데이터인지 Generator가 만들어낸 것인지 정확히 구별하는 것
최종적으로는 Generative가 실제 data와 완벽하게 동일한 데이터를 생성하여 Discriminator가 두 가지를 전혀 구별하지 못하도록 하는 것을 목표로 학습이 진행된다.
Adversarial Net
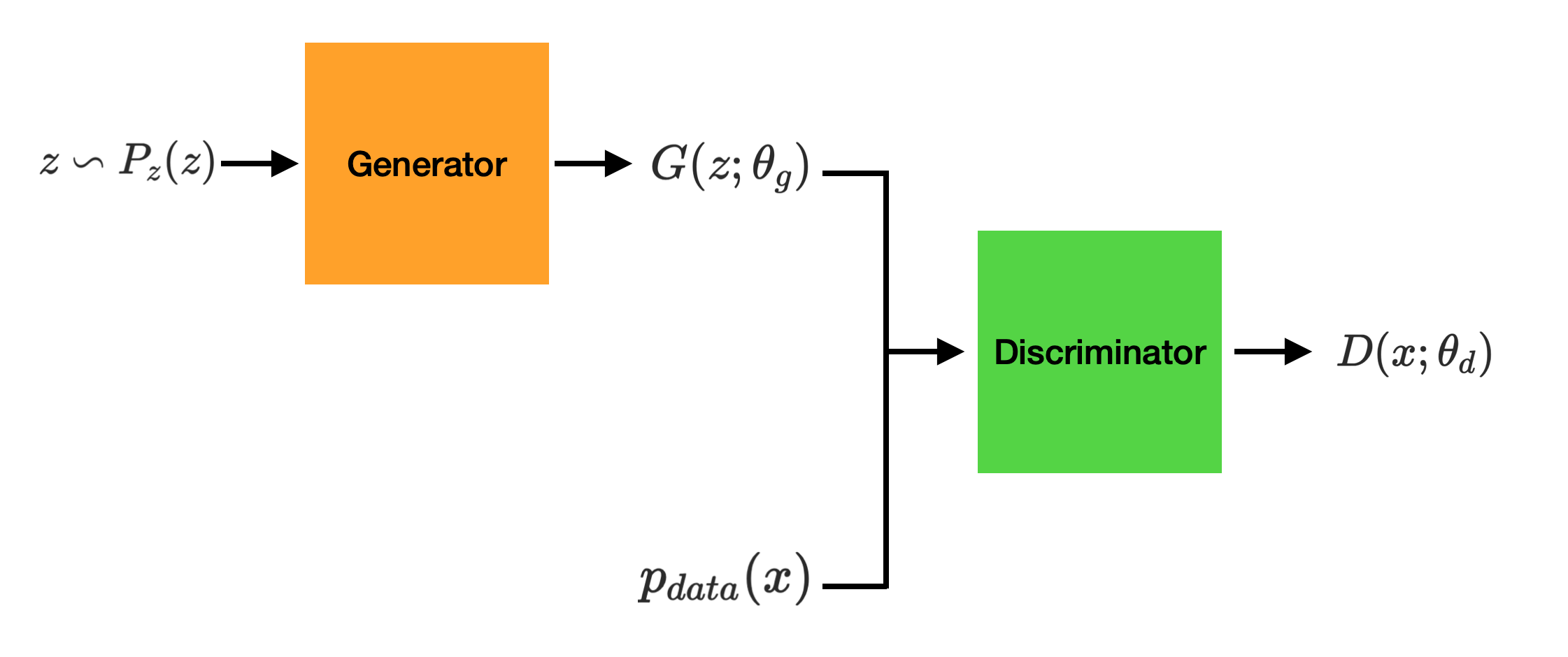
Adversarial Training의 Generator와 Discriminator를 Neural Network로 구현한 것이 Adversarial Net이다.
Generator
Generator는 실제 데이터와 유사한 데이터를 생성하는 것을 목표로 한다. 수식으로 표현하면 다음과 같다.
\[G(z; \theta_g) \qquad z \backsim P_z(z)\]즉 Generator는 prior \(P_z(z)\)에서 샘플링하여 얻어진 \(z\)를 입력으로 받아 유사 데이터 \(p_g\)를 출력하게 된다. 이때 Prior를 논문에서는 임의의 noise distribution 으로 표현하고 있으며, 구현 시에는 일반적으로 가우시안 분포를 사용한다고 한다.
Discriminator
Discriminator는 실제 데이터 \(p_{data}\)와 Generator가 만든 데이터 \(p_g\) 둘 중에 하나를 받아 구별해내야 한다.
\[D(x; \theta_d)\]입력은 실제 데이터 또는 생성 데이터이며 출력 값은 실제 데이터인 경우 1, 생성 데이터인 경우 0이 되어야 한다. 즉 Discriminator의 출력 값은 입력 데이터가 실제 데이터일 확률을 의미한다고 할 수 있다.
MiniMax Function
위의 두 가지 식을 합치면 다음과 같이 value function \(V\)에 대한 minimax 식으로 나타낼 수 있다.
\[\min_G \max_D V(D, G) = E_{x \backsim p_{data}(x)}[\log D(x)] + E_{z \backsim p_z(z)}[\log (1 - D(G(z)))]\]위 식에서 \(D\)는 언제 \(V(D, G)\)를 극대화될까. 좌변의 첫 번째 항, 즉 실제 데이터가 들어온 경우에는 \(D(x)\)가 1이 되고, 두 번째 항, 즉 Generator가 만들어 낸 데이터가 들어온 경우에는 \(1 - D(G(z))\)가 1이 되는 경우이다. 이때 \(1 - D(G(z)) = 1\)은 \(D(G(z)) = 0\)으로 바꿔쓸 수 있으므로 Discriminator \(D\)는 실제 데이터 \(x\)가 들어오면 1을, 생성 데이터 \(G(z)\)가 들어오면 0을 항상 출력할 때 \(V(D, G)\)가 극대화된다고 할 수 있다.
그렇다면 \(G\)는 언제 \(V(D, G)\)를 극소화할까. 좌변의 첫 번째 항에는 \(G\)가 포함되어 있지 않으므로 생략하고 두 번재 항을 보면 \(1 - D(G(z))\)가 0이 될 때, 즉 \(D(G(z)) = 1\)이 성립할 때 \(V(D, G)\)가 극소화된다는 것을 알 수 있다.
Global Optimality \(p_g = p_{data}\)
Adversarial Net의 최종 목표는 생성 모델 \(G\)가 만들어내는 것과 실제 데이터가 동일해지는 것이다. 즉 \(p_g = p_{data}\)가 성립하는 것으로 이해할 수 있다. 논문에서는
\[\min_G \max_D V(D, G) = E_{x \backsim p_{data}(x)}[\log D(x)] + E_{z \backsim p_z(z)}[\log (1 - D(G(z)))]\]에 따라 모델을 업데이트하게 되면 \(p_g = p_{data}\)가 성립할 수 있음을 수학적으로 증명하고 있다.
Proposition 1
\[\text{ For } G \text{ fixed, the optimal discriminator } D \text{ is } D^*_G(x) = { p_{data}(x) \over p_{data}(x) + p_g{(x)}}\]이를 증명하기 위해 \(V\)에 대한 식을 다음과 같이 전개할 수 있다.
\[\eqalign{ V(D, G) &= E_{x \backsim p_{data}(x)}[\log D(x)] + E_{z \backsim p_z(z)}[\log (1 - D(G(z)))] \\ &= \int_x p_{data}(x)\log D(x) dx + \int_z p_z(z)\log (1 - D(G(z))) dz\\ &= \int_x p_{data}(x)\log D(x) + p_g(x)\log (1 - D(x)) dx }\]이때 \(D\)의 값은 0부터 1 사이의 값이므로 다음과 같은 공식이 성립한다.
- \(a, b\)가 모두 0인 경우를 제외하고 \(y = a\log(x) + b\log(1-x)\)는 \([0,1]\)의 \({a \over a + b}\)에서 최대값을 가진다.
따라서 \(G\)가 변화하지 않는다면 \(D\)는 \({ p_{data}(x) \over p_{data}(x) + p_g(x)}\)에서 최대값을 가진다고 할 수 있다. 그리고 이에 따라 MinMax 형태로 되어 있는 \(V\)의 최적화 식을 다음과 같이 쓸 수 있다.
\[\eqalign {C(G) &= \max_D V(G, D) \\ &= E_{x \backsim p_{data}(x)}[\log D^*(x)] + E_{z \backsim p_z(z)}[\log (1 - D^*(G(z)))] \\ &= E_{x \backsim p_{data}(x)}[\log D^*(x)] + E_{x \backsim p_g(x)}[\log (1 - D^*(x))] \\ &= E_{x \backsim p_{data}(x)}[\log { p_{data}(x) \over p_{data}(x) + p_g{(x)}}] + E_{x \backsim p_g(x)}[\log { p_{g}(x) \over p_{data}(x) + p_g{(x)}}] }\]Theorem 1
\(C(G) = \max_D V(G, D)\)로 정리했으므로 \(C(G)\)를 \(G\)에 대해 최소화하는 것만 남았다. 이때 \(p_{data} = p_g\)가 성립할 때 \(C(G)\)가 가장 작아진다는 것은 다음과 같이 증명할 수 있다.
\[\eqalign{ C(G) &= E_{x \backsim p_{data}(x)}[\log { p_{data}(x) \over p_{data}(x) + p_g{(x)}}] + E_{x \backsim p_g(x)}[\log { p_{g} (x) \over p_{data}(x) + p_g{(x)}}] \\ &= E_{x \backsim p_{data}(x)}[\log { p_{data}(x) \over p_{data}(x) + p_g{(x)}}] + E_{x \backsim p_g(x)}[\log { p_{g} (x) \over p_{data}(x) + p_g{(x)}}] + \log 4 - \log 4 \\ &= E_{x \backsim p_{data}(x)}[\log { 2p_{data}(x) \over p_{data}(x) + p_g{(x)}}] + E_{x \backsim p_g(x)}[\log { 2p_{g} (x) \over p_{data}(x) + p_g{(x)}}] - \log 4 \\ &= \int p_{data}(x)\log { 2p_{data}(x) \over p_{data}(x)+ p_g{(x)}} dx + \int p_g(x)\log { 2p_{g} (x) \over p_{data}(x) + p_g{(x)}} dx - \log 4 \\ &= KL(p_{data} || { p_{data} + p_g \over 2}) + KL(p_{g} || { p_{dagta} + p_g \over 2}) - \log 4 }\]위의 식은 다시 Jenson-Shannon Divergence 식으로 표현할 수 있다.
\[C(G) = -\log 4 + 2 \cdot JSD(p_{data} || p_g)\]이때 Jenson-Shannon Divergence는 두 분포가 동일할 때 최소값 0을 가진다. 따라서 \(C(G)\)는 \(p_{data} = p_g\)에서 최소값 \(-\log 4\)를 가진다고 할 수 있다.
Algorithm
GAN의 알고리즘은 다음과 같다.

전체적으로 볼 때 두 파트, 즉 Discriminator를 업데이트하는 것과 Generator를 업데이트 하는 것으로 나누어 볼 수 있다. 한 번의 iteration을 돌 때 먼저 Discriminator를 업데이트하고, 이후 Generator를 업데이트하도록 되어 있으며 Discriminator를 k번 업데이트 할 때 Generator는 1번만 업데이트하는 것도 중요한 특징 중 하나라고 할 수 있다. 이는 \(G\)의 업데이트 속도를 늦춰 \(D\)를 최적의 상태(optimal solution)로 유지하도록 하기 위함이라고 한다.
논문에서는 이러한 업데이트 과정을 다음과 같이 그림으로 표현하고 있다.
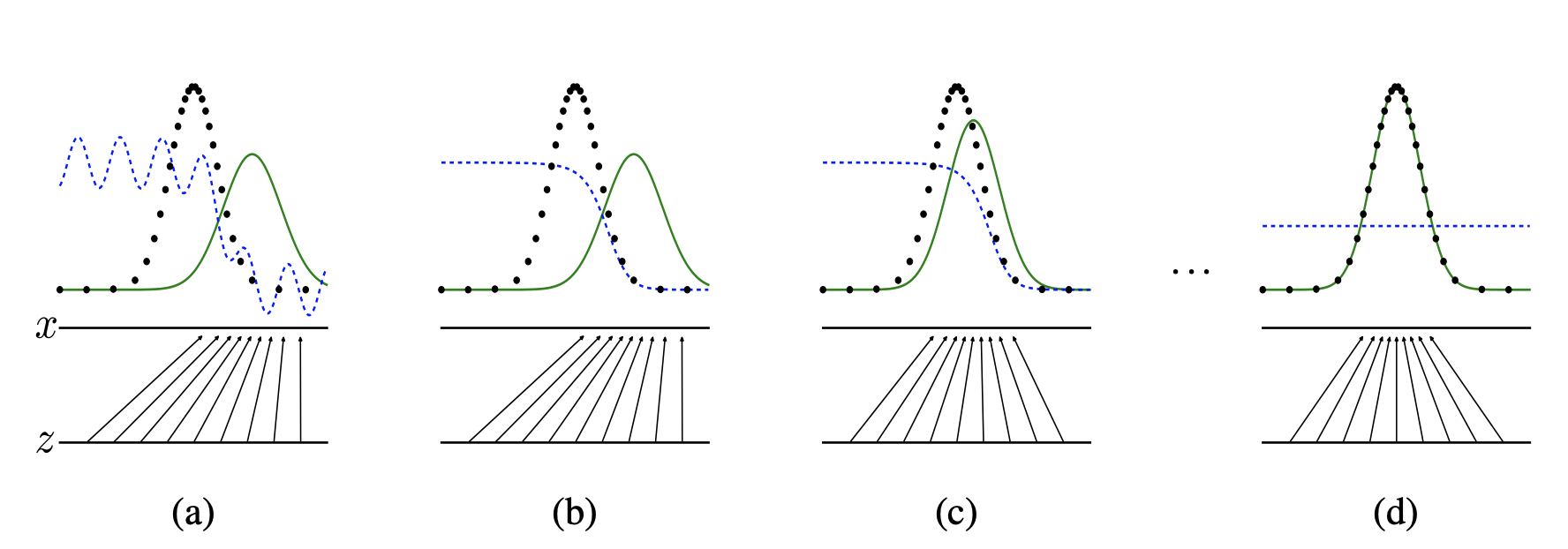
여기서 파란 점선은 Discriminator의 분포를, 초록 실선은 Generator의 분포(\(p_g\))를, 마지막으로 검은 점선은 data의 분포(\(p_{data}\))를 의미한다. 첫 번째 그림 (a)를 보게 되면 \(p_{data}\)와 \(p_{g}\)가 전혀 맞지 않다는 것을 알 수 있다. 그리고 discriminator의 경우 \(p_g\)와 \(p_{data}\)의 결정 경계를 기준으로 왼쪽은 높고 오른쪽은 낮게 표현되고 있다. 제대로 새로운 데이터를 생성하기 위해서는 생성 모델의 분포 \(p_{g}\)와 데이터의 분포 \(p_{data}\)가 (d)의 그림처럼 동일해져야 한다.
이때 알고리즘과 같이 Discriminator를 먼저 업데이트 해주게 되면 (b)와 같이 파란 점선이 최적화되어 굴곡 없이 보다 안정적으로 구별할 수 있게 된다. 그리고 이어서 Generator를 업데이트 해줌으로써 \(p_{g}\)의 분포는 \(p_{data}\)에 조금 더 다가가게 된다. 위의 그림은 이를 반복적으로 수행하면 결과적으로 최적의 상태, 즉 그림 (d)에 도달할 수 있을 것임을 보여주는 것이다.
(d)에서는 파란 점선, 즉 Discriminaotr의 분포가 어디어서나 \(1/2\)인데, 이는 어디에서나 실제 데이터와 생성 모델이 만들어낸 데이터를 구별할 수 없어 실제 데이터일 확률이 \(1/2\)로 나오는 것을 의미한다.