논문 제목 : Device Placement Optimization with Reinforcement Learning

• Azalia Mirhoseini, Hieu Pham, Quoc V. Le, Benoit Steiner, Rasmus Larsen, Yuefeng Zhou, Naveen Kumar, Mohammad Norouzi, Samy Bengio, Jeff Dean
• 2017
• 논문 링크

Summary

• 강화학습 알고리즘을 실제 Placement 문제를 해결하는 데에 적용한 논문이다.
• Policy Netwrok를 Attentional Seq to Seq 모델로 하고 있다.
• Asynchronous Distributed Training을 통해 보다 안정적이고 빠른 학습을 달성할 수 있다.

Device Placement Optimization

딥러닝의 발전은 네트워크의 크기와 비례하며 이뤄졌다고 할 수 있을 정도로 딥러닝 모델이 가지는 네트워크의 크기는 지속적으로 커지고 있다. 이에 따라 한 번 모델을 학습하는 데에도 컴퓨팅 자원을 점차 많이 필요해졌고, RAM 용량 등의 이유로 복수의 GPU를 필요로 하는 경우도 많다. 당연하게도 GPU를 여러 개 운용하는 경우 어떤 작업을 어떤 GPU에 할당할 것인지가 전체 Execution Time에 많은 영향을 미치게 된다. 예를 들어 GPU가 4개 있는 상황에서 특정 GPU에 대부분의 작업을 할당한다면 하나만을 사용할 때와 비교해 전체 작업 시간은 크게 줄어들기 어려울 것이다.

논문 제목에서 언급하고 있는 Device Placement Optimization이란 가용 자원을 가장 효율적으로 사용할 수 있도록 하기 위해 작업을 Device에 잘 할당하는 방법을 찾는 것이라고 할 수 있다. 논문에서는 이러한 문제를 Seq to Seq 구조의 Policy를 갖는 REINFORCE 알고리즘을 적용하여 해결하려 하며, 결론부터 이야기하면 기존의 일반적인 할당 방법보다 3.5배 정도 더 빠른 방법을 찾아내는 데에 성공했다고 한다.

Objective Function

딥러닝 모델을 학습시키는 것 또한 일련의 작업들의 Sequence라고 할 수 있다. 그런데 항상 수행해야 할 모든 작업들이 순차적이지는 않고 경우에 따라서는 순서를 임의로 설정하는 것이 가능하다. 이러한 점에서 작업들은 일종의 Graph로 주어진다고 볼 수 있으며, Device Placement Optimization이란 Graph 형태로 주어지는 작업들을 연산 시간 등을 고려해 각 Device에 최적으로 배분하는 방법을 찾는 것이 된다.

이를 수학적으로 표현하기 위해 논문에서는 다음과 같은 Notation을 도입하고 있다.

\(\mathcal G\)	작업 Graph
\(\{1, ..., \mathcal D \}\)	GPUs
\(\{ o_1, ... o_M \}\)	작업
\(\mathcal P = \{ p_1, ... p_M \}, \ p_i \in {1, ..., \mathcal D}\)	작업이 배치된 Device
\(\pi(\mathcal P \lvert \mathcal G ; \theta)\)	Policy
\(r(\mathcal P)\)	\(\mathcal P\) 배치를 따랐을 때 소요되는 Execution Time, Reward

이때 목표는 어떤 배치 \(\mathcal P\)에 따라 수행하는 데에 소요되는 시간 \(r(\mathcal P)\)를 최소화하는 것이 된다. 따라서 목적 함수 \(J(\theta)\)는 다음과 같이 정의할 수 있다.

\[J(\theta) = E_{\mathcal p \backsim \pi(\mathcal p \lvert \mathcal G ; \theta)} [r(\mathcal P) \lvert \mathcal G]\]

위의 목적 함수 식을 최소화하는 것이 목표이므로 이를 REINFORCE 식에 따라 Policy Gradient를 구하면 다음과 같다.

\[\nabla_\theta J(\theta) = E_{\mathcal P \backsim \pi (\mathcal P \lvert \mathcal G; \theta)} [r(\mathcal P) \cdot \nabla_\theta \log p(\mathcal P \lvert \mathcal G; \theta)]\]

만약 \(K\)개의 Sample을 뽑아 Policy Gradient 기대값을 추정한다면 다음과 같다. 여기서 \(B\)는 baseline term으로 variance를 줄여 보다 안정적인 학습을 가능하도록 하기 위해 도입되었다.

\[\nabla_\theta J(\theta) \approx {1 \over K} \Sigma_{i=1}^K (r(\mathcal P) - B) \cdot \nabla_\theta \log p(\mathcal P \lvert \mathcal G; \theta)\]

Policy Network

Policy \(\pi(\mathcal P \lvert \mathcal G ; \theta)\)를 보게 되면 Graph \(\mathcal G\)를 입력으로 받아 Sequence \(\mathcal P\)를 반환하고 있음을 알 수 있다. 즉 State는 배치 대상이 되는 작업들의 Graph이고, Action은 이들 작업을 각각의 GPU에 배치한 배치 결과가 된다. 이를 구현하기 위해 논문에서는 Policy를 아래 그림과 같이 Attentional Seqence to Sequence 구조로 구성한다.

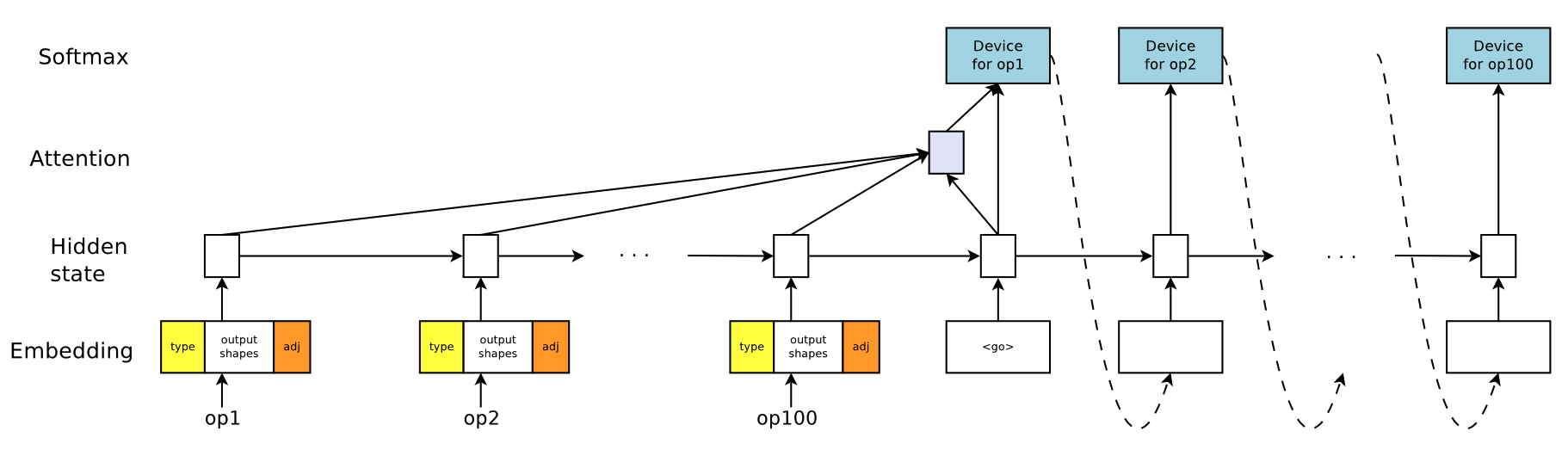
Input & Output

Policy의 입력은 위에서 언급한 대로 작업(Operation)들의 Graph이다. 이를 Sequence to Sequence 모델의 입력으로 전달하기 위해서는 개별 작업들을 Embedding 할 필요가 있다. 위의 Policy Network 이미지에서 왼쪽 하단의 입력이 그것인데, 크게 type, output shapes, adj라는 세 가지 정보를 담고 있으며 이를 Concat 한 것이라고 할 수 있다

• type: 작업의 유형(MatMul, Conv2d etc)
• output shapes: 작업의 모든 출력을 concat한 것의 size
• adj: 작업의 인접 정보

위의 정보들이 Encoder의 입력으로 들어가게 되면 Decoder의 출력으로는 입력의 길이와 동일한 Device의 Sequence \(\mathcal P = \{ p_1, ... p_M \}\)가 나오게 된다. Encoder의 첫 번째 입력으로 들어온 작업이 Decoder의 첫 번째 출력으로 나온 Device \(p_i\)에 할당되는 식이다.

Grouping

RNN 구조이므로 Sequence의 길이가 길어지면 Gradient Vanishing, Gradient Exploding 문제가 발생할 가능성이 커지고, 메모리 소모가 매우 커진다는 단점이 있다. 이를 방지하기 위해서는 Sequence의 길이를 줄일 필요가 있는데, 논문에서는 배치 대상이 되는 작업들을 TensorFlow colocation_with feature 방법과 이에 휴리스틱을 더해 그룹화하여 배치 대상의 개수를 줄였다고 한다.

Asynchronous Distributed Training

학습에 있어 특징 중 하나는 Asynchronous Distributed Training으로 학습 속도를 높인다는 점이다. 전체적으로 아래 이미지와 같은 구조를 가지고 있으며 구체적으로 (1) Controller와 worker의 관계, (2) Controller와 Parameter Server의 관계 두 가지로 나누어 생각해 볼 수 있다.

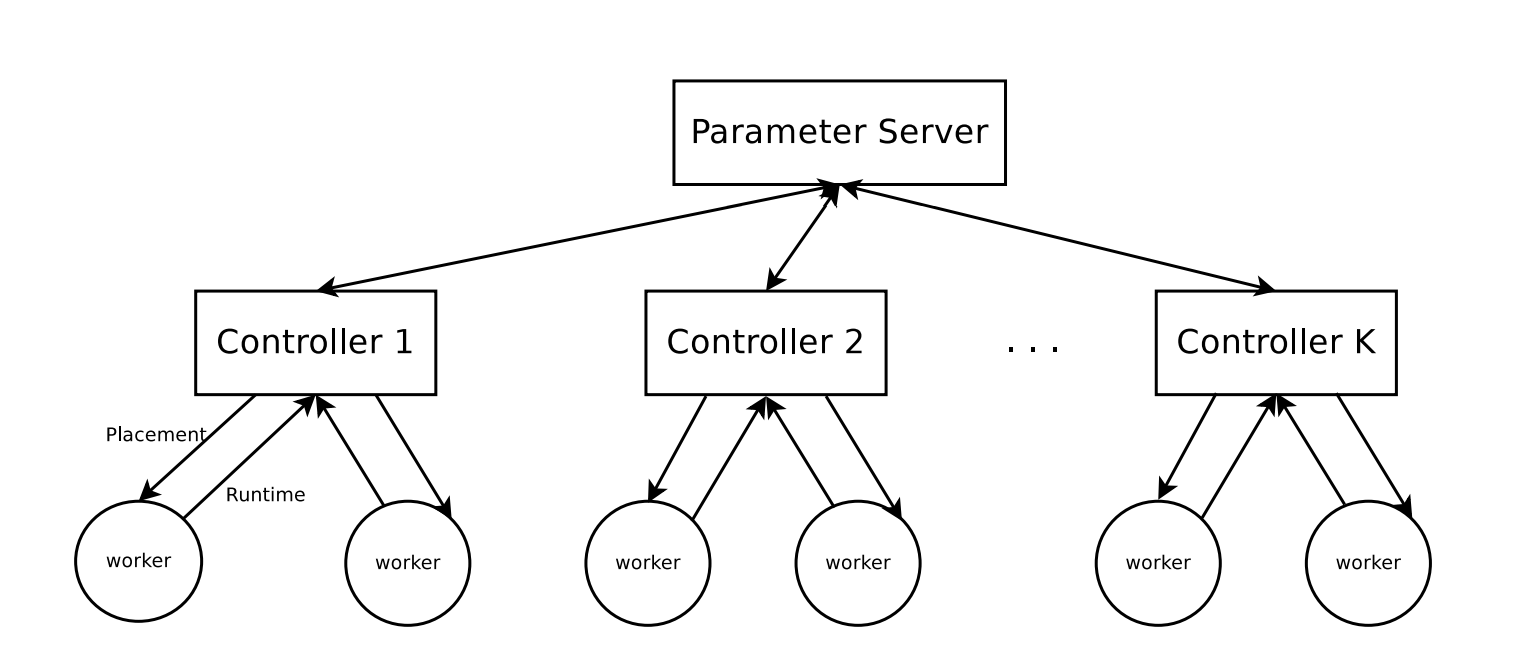
Controller - Worker

Controller는 Policy Network로서, 독립적으로 입력 Graph에 대한 출력 Placement를 샘플링할 수 있다. 현재 가지고 있는 Policy Parameter에 따라 확률적으로 구한 복수의 Placement를 Worker에 분배하면 Worker는 Placement에 따라 실제로 작업을 수행하고 Runtime, 즉 Reward Signal을 다시 Controller에 보내게 된다. Policy Gradient 방법에 따라 Policy를 업데이트하기 위해서는

\[\nabla_\theta J(\theta) \approx {1 \over K} \Sigma_{i=1}^K (r(\mathcal P) - B) \cdot \nabla_\theta \log p(\mathcal P \lvert \mathcal G; \theta)\]

식을 정확하게 추정하는 것이 중요하다. 여기서 Worker의 숫자가 \(K\)가 되므로, Worker가 많으면 많을수록 현재 Controller가 가지고 있는 Policy Parameter \(\theta\)의 Gradient를 보다 정확하게 추정할 수 있다. 논문 실험에서는 20개의 Controller 각각에 4~8개의 Worker를 붙여 진행했다고 한다.

Reducing Variance

Controller 마다 복수의 Worker를 가지고 있어 Gradient의 Variance가 줄어드는 효과를 얻을 수 있다. 하지만 시뮬레이터 환경이 아닌 실제 GPU 환경에서 학습이 이뤄지기 때문에 학습 과정에서 Noise가 발생할 여지가 매우 크다. 정확한 Reward 계산을 위해 개별 Worker는 하나의 Placement를 10회 반복 수행하고, 이것의 Moving Average가 가장 작은 경우를 Execution Time으로 Controller에 전달한다.

Controller - Parmater Server

Controller가 Worker들이 계산한 Execution Time을 수집하여 Gradient를 구한 후에는 이를 사용하여 Parameter Server에 저장되어 있는 Controller Parameter를 비동기적으로 업데이트하게 된다.