논문 제목 : Chip Placement with Deep Reinforcement Learning
- Azalia Mirhoseini, Anna Goldie, Mustafa Yazgan, Joe Jiang, Ebrahim Songhori, Shen Wang, Young-Joon Lee 등
- 2020
- 논문 링크
Summary
- 반도체 설계에 있어 중요한 단계 중 하나인 Chip Placement 문제를 강화학습으로 해결하는 논문으로, 현재 업계에서 사용되는 방법보다 더 빠르고 좋은 결과물을 도출할 수 있다고 한다.
- 도메인 지식에 근거하여 Reward 및 Constraint를 Wire Length, Placement Density, Routing Congestion로 설정하며, 이를 통해 PPA(Power, Performance, Area)를 기준으로 최적 배치를 달성하는 것을 목표로 한다.
- 네 가지 유형의 정보를 State로 받고 있으며, 각각의 의미를 정확히 파악하기 위해 논문에서 제안하는 Graph Neural Network를 사용한다. 또한 넓은 State Space에 대응하기 위해 Transfer Laerning을 적용하고 있다.
Keywords
- Chip Netlist
- Macro and Standard Cell
- WireLength
- Routing Congestion
- Placement Density
- Chip Canvas
Chip Placement Problem
Chip placement는 반도체 설계 과정에서 가장 복잡하고 시간이 오래 걸리는 작업 중 하나이다. Chip Placement Problem은 다음과 같이 정의되는 최적화 문제라고 할 수 있다.
- 배치의 대상은 크게 Macro(SRAM)와 Standard Cell(LOGIC GATE)이다.
- PPA(Power, Performance, Area)를 기준으로 최적 배치를 달성해야 한다.
- Placement Density와 Routing Congestion이 적으면 적을 수록 좋다.
- Netlists Graph가 크면 클수록 문제의 복잡도는 높아진다.
논문에서는 전문가가 몇 주간 처리해야 하는 작업을 6시간 내에 해결하면서도 성능이 비슷하거나 더 나은 방법을 제시하고 있다. 이를 통해 강화학습을 반도체 설계에 적용하는 새로운 가능성을 보여주고 있다.
What is the target of placement?
Chip Placement에서 해결해야 하는 것은 아래 두 가지 요소를 적절히 배치하는 것이다.
1. Standard Cell
NAND Gate, NOR Gate 등과 같이 가장 기본적인 수준의 기능을 제공하는 구성요소들을 말한다.
2. Macro
SRAM, 레지스터 등과 같이 고유의 기능을 가지고 있으면서 기능,효율 상의 이유 또는 외부 IP 구매 계약 상의 이유로 설계가 고정적인 덩어리를 말한다. Macro 자체가 수백 수천 개의 Standard Cell로 구성되기 때문에 Standard Cell과 비교해 크기가 크다.
What is Good Placement Design?
반도체 설계에서 좋은 Placement Design이란 Power, Performance, Area 세 가지 모두에 대해 최적화를 달성한 Design이라고 할 수 있다. 즉 전력 소모가 적을수록, 성능이 높을수록(클럭 등), 배치 면적이 좁을 수록 좋다. 그런데 이 세 가지를 매번 계산하는 것은 시간이 오래 걸리는 등 비용이 높기 때문에 효율성을 위해 설계 과정에서 상대적으로 쉽고 빠르게 계산할 수 있는 지표들로 대신하곤 한다. 논문에서는 이러한 지표들로 다음 세 가지를 제시하고 있으며, 알고리즘 또한 아래 세 가지를 기준으로 학습한다.
1. WireLength
반도체를 구성하는 Macro와 Standard Cell이 작동하기 위해서는 Power Supply, Clocks, Signal을 위한 Wire가 필요하다. 이때 각 요소를 연결하는 Wire의 길이(WireLength)가 짧으면 짧을수록 빠르게 전달할 수 있으므로 전력 소모와 속도의 면에서 우수하다고 볼 수 있다.
2. Routing Congestion
또한 제한된 크기의 Chip Canvas 상에서 라우팅 자원은 한정적이므로 적절하게 라우팅 자원을 분배하는 것이 중요하다. 이때 일정한 영역 내에 연결해야 하는 요소의 갯수가 많아지면 많아질수록 라우팅 자원은 부족해질 수밖에 없고, 그 결과 전체적인 설계의 질에 악영향을 미치게 된다. 따라서 Chip Canvas의 부분 영역 상에서 일정 수준 이하의 라우팅 혼잡도(Routing Congestion)를 유지하는 것이 중요하다.
3. Placement Density
한 가지 더 중요한 것이 있다면 Macro와 Standard Cell 등 Chip Canvas 상에 배치되는 요소들이 서로 가까우면 안된다는 것이다. 이를 만족하지 못하는 반도체가 정상적으로 작동하지 않을 가능성이 높아지므로 밀집도(Placement Density)가 일정 수준 이상 높아지는 경우는 없어야 한다.
Formulated as MDP
강화학습을 적용하기 위해서는 문제의 MDP(Markov Decision Process)를 정의해야 한다. 논문에서 정의하고 있는 MDP의 구성요소 \((S, A, P_{s,s'}, R, \gamma)\)는 다음과 같다.
1. state \(S\)
Chip Canvas 상에 Netlist 구성요소들을 놓을 수 있는 모든 경우의 수로 정의한다. 구체적으로 State는 다음 네 가지 정보를 포함한다.
- Netlist의 Graph Embedding: Adjecency Matrix
- 배치할 Node의 특성: Width, Height, Type etc
- Netlist에 대한 메타 정보: Routing Allocations, Totla Number of Wire, Macros, Standard Cell Cluster
- Feasibiliy Mask: 현재 Node를 배치할 수 있는 Grid Cell에 대한 정보
그리고 첫 번째 State \(s_0\)은 어떠한 Macro도 배치되지 않았을 때를 의미한다.
2. action \(A\)
Chip Canvas 상에 Macro를 놓을 수 있는 위치들의 집합으로 정의한다. 따라서 매 시점 선택 가능한 Action이 달라진다.
3. state transition \(P_{s,s'}\)
Chip Canvas에서 특정 Action \(a\)를 선택하여 Macro를 배치했을 때 어떠한 State를 가지게 될 것인지로 정의한다.
4. reward
강화학습에서 Reward는 매 시점에 이전 시점의 State와 Action에 따라 결정된다. 논문에서는 WireLength와 Congestion에 따라, 즉 최적화 수준에 따라 Reward를 받는 방법을 제시하고 있다.
Reward Function
강화학습은 안정적인 성능을 확보하기 위해서 필요로하는 학습 횟수가 매우 많은 편이기 때문에 Reward Function의 계산이 빠르고 정확해야 한다. 이와 관련하여 무엇을 기준으로 Reward를 계산할 것인지가 문제되는데 논문에서는 측정 속도가 빠르면서도 전력 소모 및 성능에 영향을 미치는 WireLength를 Reward를 계산한다. 이와 함께 Chip의 안정성에 큰 영향을 미치는 Routing Congestion도 Reward를 계산하는 데에 사용한다. 구체적으로 Reward Function이 계산되는 과정은 다음과 같다.
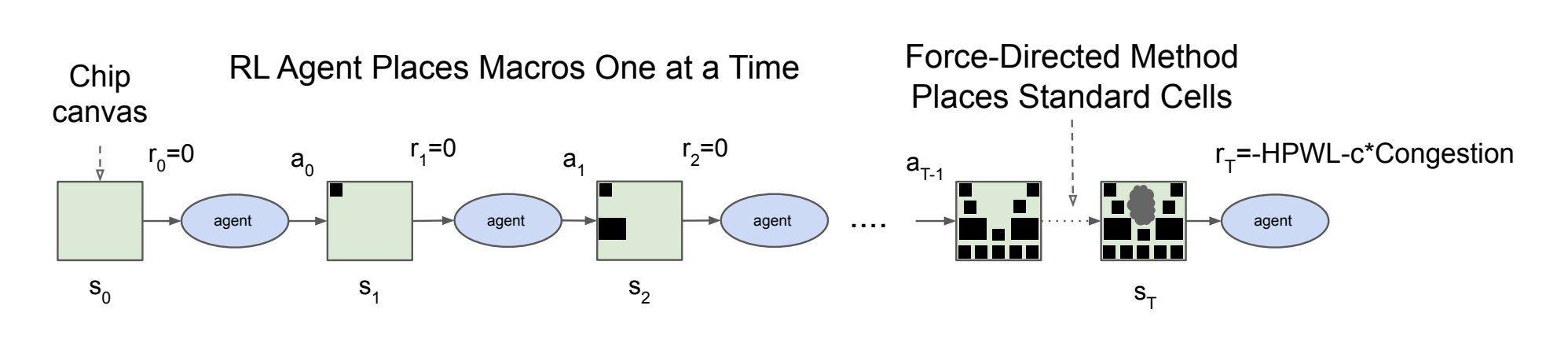
- Chip Canvas를 Grid로 수천 개의 Grid Cell로 이산화한다.
- 강화학습 알고리즘(PPO)에 따라 Macro를 각 Grid Cell 중심에 배치한다.
- Force-Directed 방법에 따라 Standard Cell을 남은 Grid Cell 중심에 배치한다.
- WireLength의 계산을 단순화하기 위해 Standard Cell과 연결되는 Wire는 모두 해당 Standard Cell이 포함된 Cluster의 중심에서 출발한다고 가정한다.
- Congestion Cost의 계산을 단순화하기 위해 평균적인 혼잡도가 상위 10% 이상인 Grid Cell에 대해서만 측정한다.
- 계산된 WireLength와 Congestion Cost로 최종 Reward를 산출한다.
Reward Calculation
모든 강화학습 알고리즘이 그러하듯 여기서도 Return(Episode Reward)을 극대화하는 것이 목표가 된다. 이때 하나의 에피소드 단위는 크기가 \(K\)인 Netlist \(g\)가 되며, 전체 Netlist \(G\)에 대해 다음과 같이 기대 Return을 극대화하는 것이 Chip Placement의 Objective Function이 된다.
\[J(\theta, G) = {1 \over K} \Sigma_{g \backsim G} E_{g,p \backsim \pi_\theta} [R_{p,g}]\]이때 마지막 Time step에 받는 Reward는 아래와 같이 계산되며 이외의 Reward는 모두 0으로 한다.
\[R_{p,q} = -\text{WireLength}(p, g) - \lambda \text{Congestion}(p, g) \\ \text{S.t. } \text{density}(p,g) \leq \max_{\text{density}}\]논문에서는 \(\lambda = 0.01\), \(\max_{\text{density}} = 0.6\)으로 설정하고 실험을 진행했으며 개별 항의 계산 방법은 아래와 같다.
1. WireLength
WireLength를 빠르게 계산하기 위해 Shahookar & Mazumder가 제시한 Half-Perimenter WireLength(HPWL)을 사용한다. HPWL은 Netlist에 포함되어 있는 모든 노드들의 경계 상자의 절반으로 정의된다.
2. Routing Congestion
Routing Net은 각 Grid Cell의 Routing Resoure를 점유하게 된다. 논문에서는 Routing Congestion를 계산하기 위해 개별 Grid Cell의 수평/수직 할당량을 추적했고, 이 과정에서 \(5 \times 1\) Convolution filter를 수평/수직 방향으로 적용했다고 한다. 또한 Routing이 모두 완료된 이후에는 MAPLE의 ABA10이라는 메트릭을 적용하여 상위 10%의 혼잡도의 평균을 최종적인 혼잡도 계산에 사용했다고 한다.
3. Placement Density
Placement Density는 Hard Constraint, 즉 밀집도가 일정 수준 이상으로 올라갈 가능성이 있으면 해당 영역에 배치를 하지 못하도록 Poliy Network의 선택을 제한하는 방식으로 적용된다. 이렇게 하므로서 논문에서는 다음 두 가지의 이점을 가질 수 있다고 언급한다
- 유효하지 않은 결과물이 나올 가능성을 줄인다.
- 최적화 문제의 Search Space를 줄인다.
과정상 Policy Network가 먼저 Macro를 배치하게 되므로 이후 배치될 Standard Cell을 배치할 위치도 고려해야 한다. 이를 위해 Density Threshold \(\max_{\text{density}}\)를 0.6으로 설정하고 실험을 진행했다고 한다. 그리고 Binary Mask를 적용하여 Density Threshold를 넘어선 Grid Cell은 선택이 불가능하도록 하여 Policy의 Action을 제한하게 된다.
Grid & Order
논문에서는 Chip Placement 문제를 강화학습에 적용 가능하도록 구체화하고 강화학습 알고리즘이 이를 보다 잘 학습할 수 있도록 하기 위해 여러 방법론들을 적용하고 있다. 그 중 Grid를 어떻게 설정할 것인지와 Macro의 배치 순서는 어떻게 되는지에 대해서는 다음과 같이 설정하고 있다.
Grid
Chip Canvas를 행과 열로 나눌 것인지는 최적화 문제의 복잡도와 설계의 질에 직접적인 영향을 미치기 때문에 중요하다. 이를 위해 논문에서는 행과 열의 최대 개수를 128개로 제한한 뒤, 이를 Bin Packing 문제로 보고 각각의 시도에서 낭비되는 공간의 크기를 계산했다고 한다.
Macro Order
Macro를 어떠한 순서대로 배치할 것인지 또한 중요하다. 이와 관련하여 논문에서는 다음 두 가지 조건을 제시한다.
- 큰 것을 먼저 배치한다.
- 위상 정렬, 즉 그래프의 선행 순서를 유지한다.
큰 것을 먼저 배치하므로써 이후 시점에 큰 것을 배치할 공간이 부족한 경우를 최소화하고, 위상 정렬을 따름으로써 Policy Network가 서로 연결된 노드를 가까이에 배치하면 좋다는 것을 학습하도록 도울 수 있다고 한다.
Model Architecture
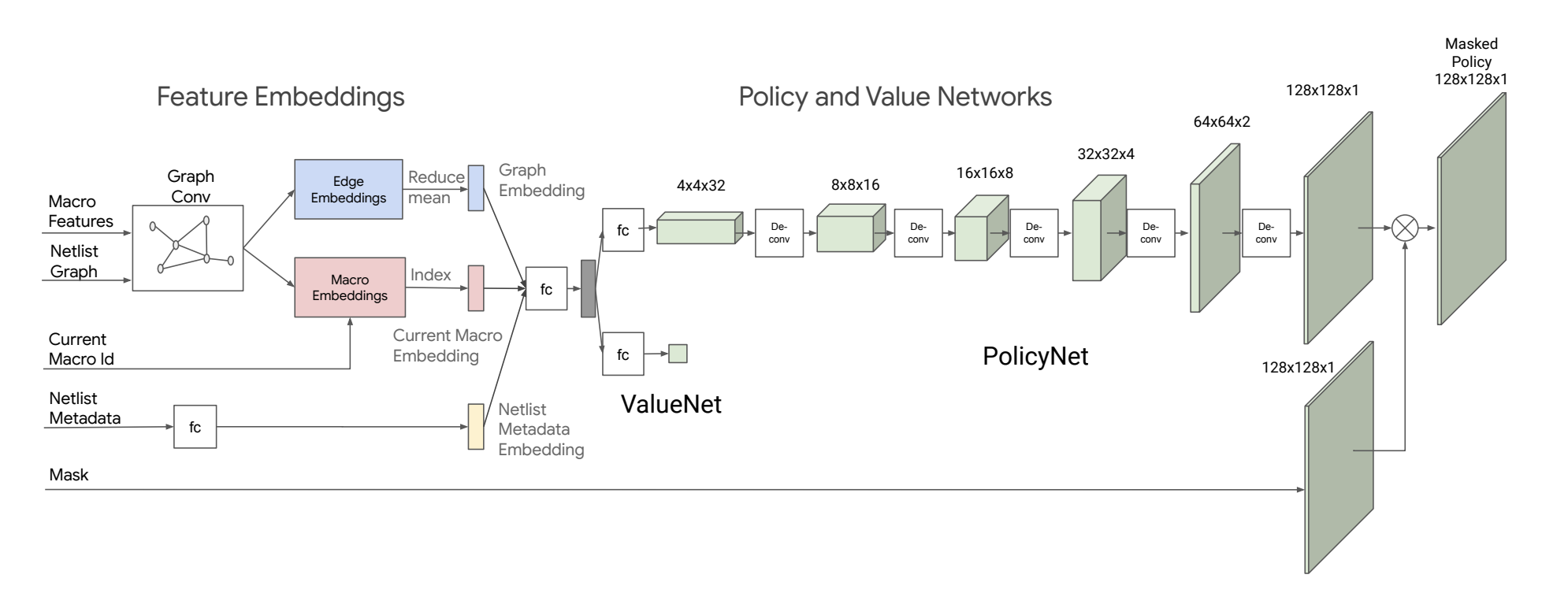
Feature Embeddings: Transfer Learning with Supervised Model
강화학습 알고리즘을 단순화한다면 어떤 state \(s\)를 보고 가장 좋을 것으로 기대되는 action \(a\)를 선택하는 것이다. 논문에서 다루고 있는 Chip Placement 문제 또한 Action이 Grid 상의 한 점을 선택하는 것일 뿐, 좋은 Action을 선택하기 위해서는 현재 Agent가 처해있는 상황에 대한 정보인 state \(s\)를 정확하게 이해하는 것이 중요하다. 논문의 표현을 빌리자면 Representation of State Space에 대해 모델이 학습을 해야 한다. 하지만 Chip Placement 문제에서는 다음 두 가지 이유 때문에 이를 달성하는 것이 쉽지 않다.
- Netlist와 Grid의 조합에 따라 너무 많은 것이 달라진다.
- 하나의 Netlist, Grid Setting에 대해 가능한 배치의 경우의 수가 많다.
Policy Network가 정확하게 State를 판단하기 위해서는 Feature Embeddings에서 본 적이 없는 State에 대해서도 충분한 의미를 추출할 수 있어야 한다. 이를 위해 논문에서는 Transfer Learning을 도입하여 Feature Embeddings를 다양한 Netlist, Grid, Placement에 대해 미리 학습시키고 이를 전이하는 방법을 사용한다.
Dataset for Supervised Model
구체적으로 논문에서는 State를 받아 그에 따른 Reward를 예측하는 Supervised Model을 Pre-Training하는 방법으로 접근한다. Supervised Model이므로 각각의 Chip Placement State와 이에 매치되는 Reward로 구성된 Dataset을 확보해야 한다. 이를 위해 5개의 서로 다른 Netlist를 사용하여 2,000번의 배치를 수행하게 되는데 이 과정에서 다양한 Placement의 경우의 수를 확보하기 위해 다음 세 가지를 적용했다고 한다.
- 초기화된 Policy Network부터 학습이 되는 과정 상의 모든 Placement Result를 수집하여 질적으로 다양한 경우를 보게 한다.
- Routing Congestion Weight \(\lambda\)를 0과 1사이의 값 중에서 다양하게 설정한다.
- Seed를 랜덤으로 한다.
그리고 각 Placement Result에 대한 Label은 Reward Function에서 언급한 것과 마찬가지로 WireLength와 Routing Congestion의 가중 합으로 구하게 된다.
Architecture of Feature Embeddings
State의 특성을 추출하는 Feature Embedding은 다음과 같이 세 단계로 이뤄져 있다.
(1) Node Feature & Node Adjacency
우선 전체 Netlist와 배치의 대상이 되는 Macro에 대해서는 다음과 같은 Graph Neural Network를 사용하여 의미를 추출한다.
- 개별 Node의 타입, 폭, 높이, x-y 좌표값을 concat하여 Vector 형태로 표현한다.
- Node Vector와 Node Adjacency Matrix를 사용하여 아래 수식을 따라 \(v, e\)를 반복적으로 업데이트한다.
- \(i,j\) 번째 Node를 연결하는 Edge \(e_{ij}\)는 \(v_i\), \(v_j\)를 Fully Connected Network \(fc_0\)에 각각 통과시켜 얻은 출력값과 Edge별 \(1 \times 1\)의 웨이트 \(w^e_{ij}\)를 모두 Concat하고, 이를 \(fc_1\)에 통과시켜 얻은 출력값으로 업데이트 한다.
- Node \(v_i\)는 자신과 연결되어 있는 모든 Edge의 Feature \(e_{i,j}\)값의 평균으로 업데이트한다.
이러한 과정을 통해 두 가지를 얻을 수 있는데, 하나는 Model 이미지에서 파란 색으로 표현되는 Edge Embeddings이고, 다른 하나는 빨간 색으로 되어있는 Macro(Node) Embeddings이다.
(2) Feature Embeddings: Netlist MetaData
Nelist MetaData는 다음과 같은 정보들로 구성되며 Fully Connected Network로 정보를 추출하게 된다.
- Horizontal and Vertical Routing Capacity
- Total Number of Edges, Macro, Standard Cell Clusters
- Chip Canvas Size
- Number of Row and Columns of Grid
(3) Concatnation
Feature Embedding의 마지막 단계는 지금까지 언급한 Edge Embeddings, Macro Embeddings, Netlist MetaData Embeddings를 모두 Concat하여 State Embedding을 만드는 것이다. 이때 Edge Embeddings와 Macro Embeddings는 통째로 사용하지는 않고 Edge Embeddings의 경우 reduce mean한 결과값을, Macro Embeddings에서는 현재 Macro Id에 맞는 정보만을 사용한다.
Training Feature Embeddings
Feature Embeddings에 대한 학습은 regression으로 각 Placement에 대한 오차가 최소화가 되도록 하는 방향으로 이뤄진다.
Policy Network
Policy Network는 State의 정보가 담긴 State Embedding을 받아 적절한 Action, 즉 Macro를 배치할 Grid Cell을 정하는 역할을 한다. Policy Network의 출력값은 각 Action을 선택할 확률 분포가 되는데, 이를 위해 State Embedding을 Fully Connected Network에 통과시킨 후 5개의 DeConvolition Network와 Batch Normalization을 반복적으로 적용하여 Grid Cell과 동일한 크기를 출력하게 된다.
최종 Action은 각 Grid Cell 중 선택할 확률이 가장 높은 것으로 결정되는데, 이때 이미 배치되어 있거나 기술적인 이유로 배치해서는 안 되는 Grid Cell은 배제해야 하므로 Mask를 적용하여 이들이 선택되지 못하도록 한다.
Experiments & Results
논문에서는 제시하고 있는 방법론과 관련하여 다양한 실험을 진행하고 그 결과를 정리하고 있다. 배치 대상이 되는 Google TPU의 구체적인 사양에 관해서는 보안 문제로 공개하지 않고 있으며, TPU 한 블럭 당 수백 개의 Macro Module과 수백만 개의 Standard Cell이 있다고만 되어 있다.
Pre-Training
첫 번째는 Feature Embedding을 위해 Pre-Training이 효과적인지 검증하는 실험이다. 이를 위해 논문에서는 다음 네 가지 경우에 대한 실험 결과를 비교하고 있다.
| Setting | Pre-Training | Fine Tuning |
|---|---|---|
| Zero-Shot | O | X |
| 2hr Fine Tuning | O | O(2Hour) |
| 12hr Fine Tuning | O | O(12Hour) |
| 24hr From Scratch | X | X |
결과는 다음과 같다. y축이 Placement Cost이므로 작으면 작을 수록 좋다.
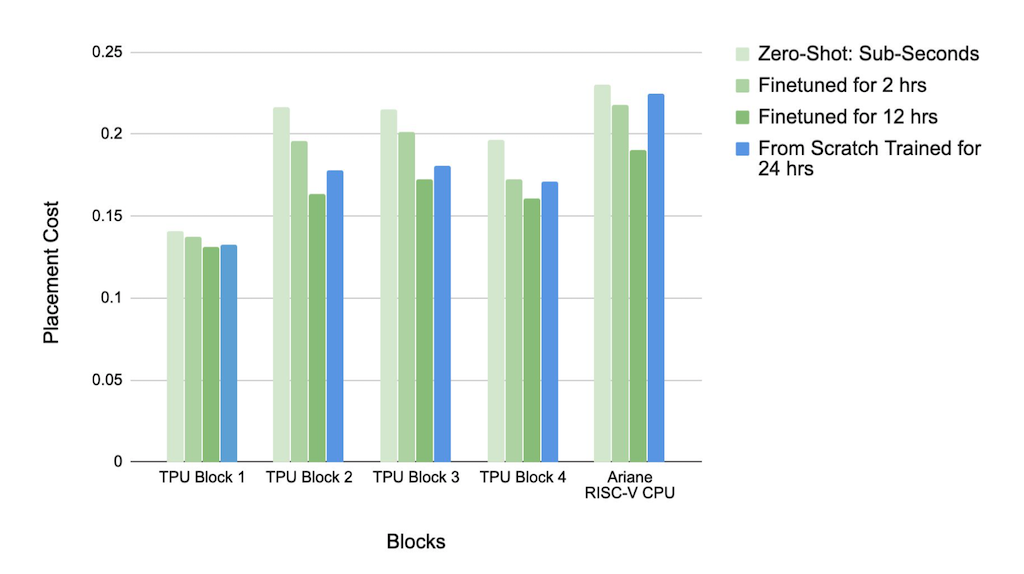
x축의 오른쪽으로 갈수록 문제의 복잡도가 높아진다. 가장 왼쪽의 TPU Block 하나만 가지고 Test를 진행한 경우에는 성능 차이가 크지 않으나 문제가 복잡해질수록 각각의 성능 차이가 커진다는 것을 알 수 있다. 모든 경우에서 성능은 12시간 동안 Test 문제에 대해 Fine Tuning을 실시한 Pre-trained Model이었다.
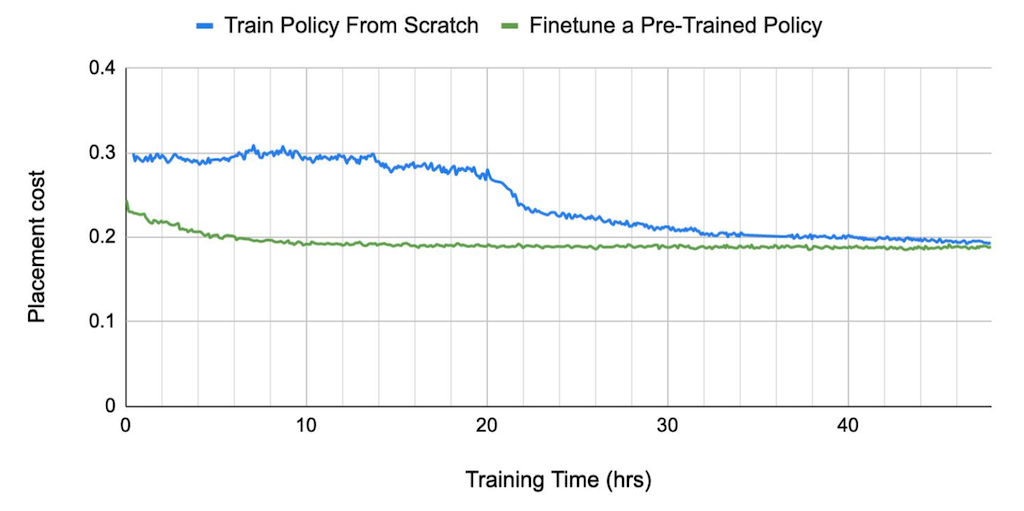
그리고 성능 뿐만 아니라 수렴 속도와 관련해서도 Pre-Trained Model을 사용하는 것이 좋다고 한다. 위의 그림을 보면 초록선으로 표현되는 Pre-Trained Model이 파란선의 From-Scrach 방법보다 더 빠르게 수렴하고 있음을 보여준다. From Scratch를 24시간으로 설정하여 비교한 것 또한 수렴 속도가 느려 보다 적은 학습량으로는 성능을 확보하기 어려웠기 때문이라고 한다. 이러한 점에서 Test Dataset 뿐만 아니라 다른 Design에 대해서도 학습하는 것이 성능과 학습 속도에 중요한 요인이 된다.
Large Dataset
다른 Design에 대해 학습하는 것이 성능과 학습 속도에 영향을 미친다면 Pre-Training에 사용하는 데이터 셋의 크기 또한 학습의 양상에 중요한 요인이 될 수도 있을 것이다. 논문에서는 이와 관련하여 TPU Block의 갯수를 2, 5, 20 Block으로 하여 실험을 진행했다고 한다.
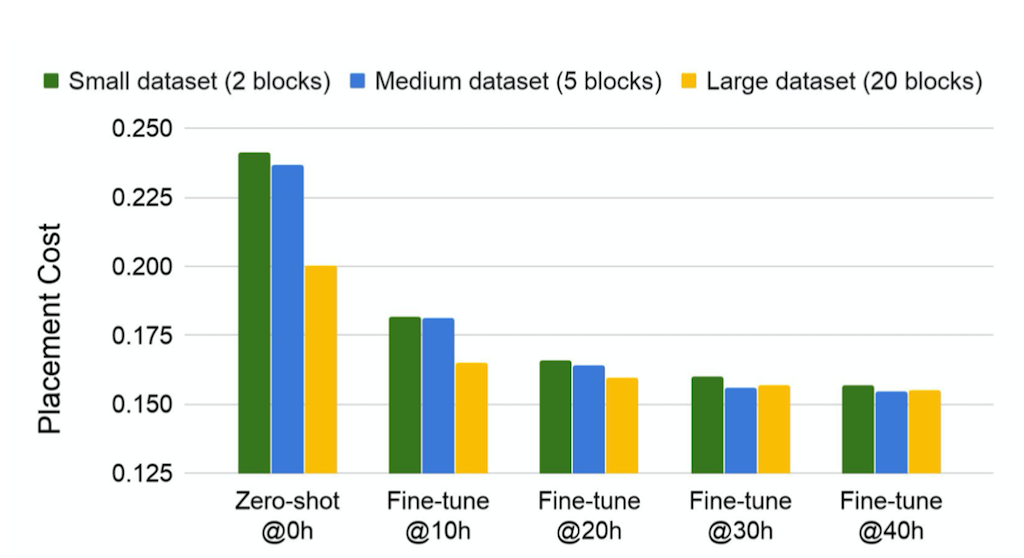
결과를 보게 되면 거의 모든 경우에서 Train Set의 크기가 클수록 성능이 높은 경향을 보이며 Fine-Tuning을 적게 수행했을 때 그 차이가 더욱 도드라진다. 이에 대해 논문에서는 Train Set의 크기가 작으면 OverFitting 문제가 생기는 것으로 보며, Policy Network에 다양한 Block의 가능성을 보여줘야 Train Set에 OverFitting 되는 문제를 방지하고 Test Set으로 들어오는 새로운 Data에 대해서도 잘 해결할 수 있다고 언급한다.
Comparing with Other Methods
마지막으로 SOTA로 알려져 있는 RePLAce와 논문에서 제시하는 방법, 그리고 전문가가 직접 수행하는 방법으로 나누어 비교하는 실험을 진행하였고, 아래와 같은 결과를 얻었다고 한다. 참고로 Ours로 표기된 것이 논문에서 제시하고 있는 방법을 사용한 것으로, 20개의 TPU Block을 대상으로 Pre-Training을 진행하고 5개의 Test TPU Block에 대해 FineTuning 한 것이라고 한다. 그리고 Manual이 전문가 팀이 직접 EDA tool을 사용하여 반복적으로 개선하여 얻은 결과이다.
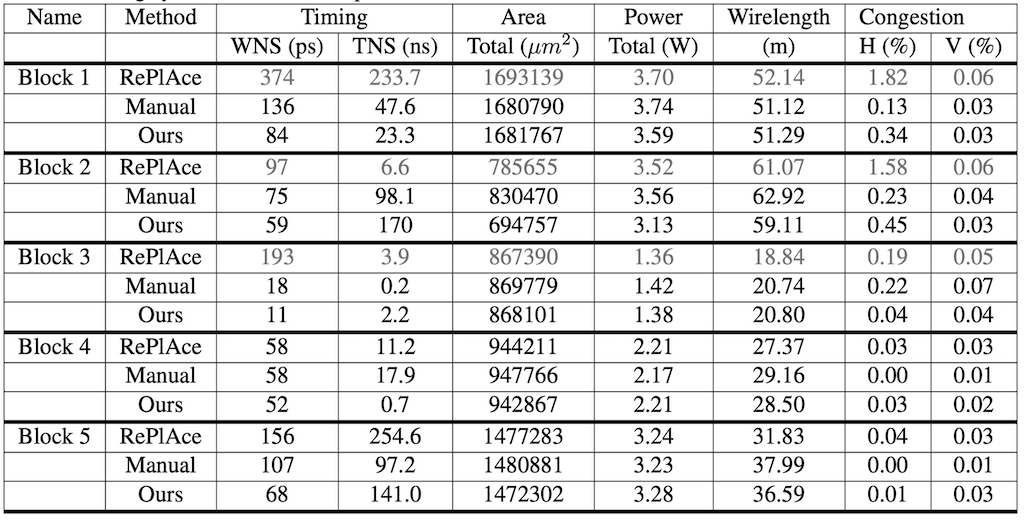
Table을 처음 보았을 때 RePLAce가 더 좋은 것 같아 보이지만 논문에서는 (당연히도) 자신들이 제시하고 있는 방법이 더 좋다(outperform)고 주장한다. 이와 관련하여 반도체 기술상 WNS가 100ps 이상이거나 Horizontal/Vertical Congestion이 1%를 넘기면 적용이 불가능한데, Block 1,2,3에서 회색으로 표기된 RePLAce의 경우 이를 초과하고 있기 때문에 사용할 수 없기 때문이라고 언급하고 있다. RePLAce 방법론의 장점 중 하나는 학습 시간이 적게 걸린다는 것으로 논문의 방법이 3~6시간 정도 걸리는 데 반해 RePLAce는 1~3.5시간이면 학습이 완료된다고 한다.
Oppertunity
논문에서 제시하고 있는 방법은 Standard Cell을 배치하는 데 있어 속도를 이유로 Force-Directed Method를 사용했으나 RePLace, DREAMPlace 등과 같이 최신의 배치 알고리즘을 사용하면 보다 성능이 높아질 것으로 기대할 수 있다.
Additional Study
- Force-Directed Method에 대해서는 VLSI Cell Placement Technique논문 리뷰에 정리해 두었다.