ROC Curve for Binary Classification

• update date: 2020.03.22

Binary Classification

이진 분류 문제는 class가 2개 있는 상황에서의 분류 문제를 말한다. 이진 분류 문제의 대표적인 예로 의사가 X-ray를 보고 암 환자를 판별하는 경우를 생각해 볼 수 있다. X-ray 사진을 보며 의사가 환자에게 말하는 상황에서는 경우의 수가 총 4가지가 있다. 즉, 암환자의 사진을 보고 암환자로 판별하거나 건강한 사람으로 판별하는 2가지 경우가 있을 것이고, 정상인의 사진에 대해서도 똑같이 2가지 경우를 생각해 볼 수 있다. 통계적으로는 이를 True Positive, False Positive, True Negetive, False Negative 라고 표현한다.

TP / TN / FP / FN

True Positive	실제 Postive에 대해 Positive로 예측한 경우
False Positive	실제 Negative에 대해 Positive로 예측한 경우
True Negetive	실제 Negative에 대해 Negative로 예측한 경우
False Negative	실제 Postive에 대해 Negative로 예측한 경우

쉽게 말해서 앞의 True / Positive 는 예측의 옳고 그름을 의미한다. 예측이 맞으면 True, 틀리면 False이다. 뒤의 Positive / Negative는 예측 값을 나타낸다.

Confusion Matrix

confusion matrix란 아래 그림과 같이 binary classification에서 예측 값과 실제 값의 경우의 수를 나타내는 매트릭스라고 할 수 있다. Confusion matrix를 사용하면 True Positive, False Positive, True Negetive, False Negative를 보다 직관적으로 이해할 수 있다.

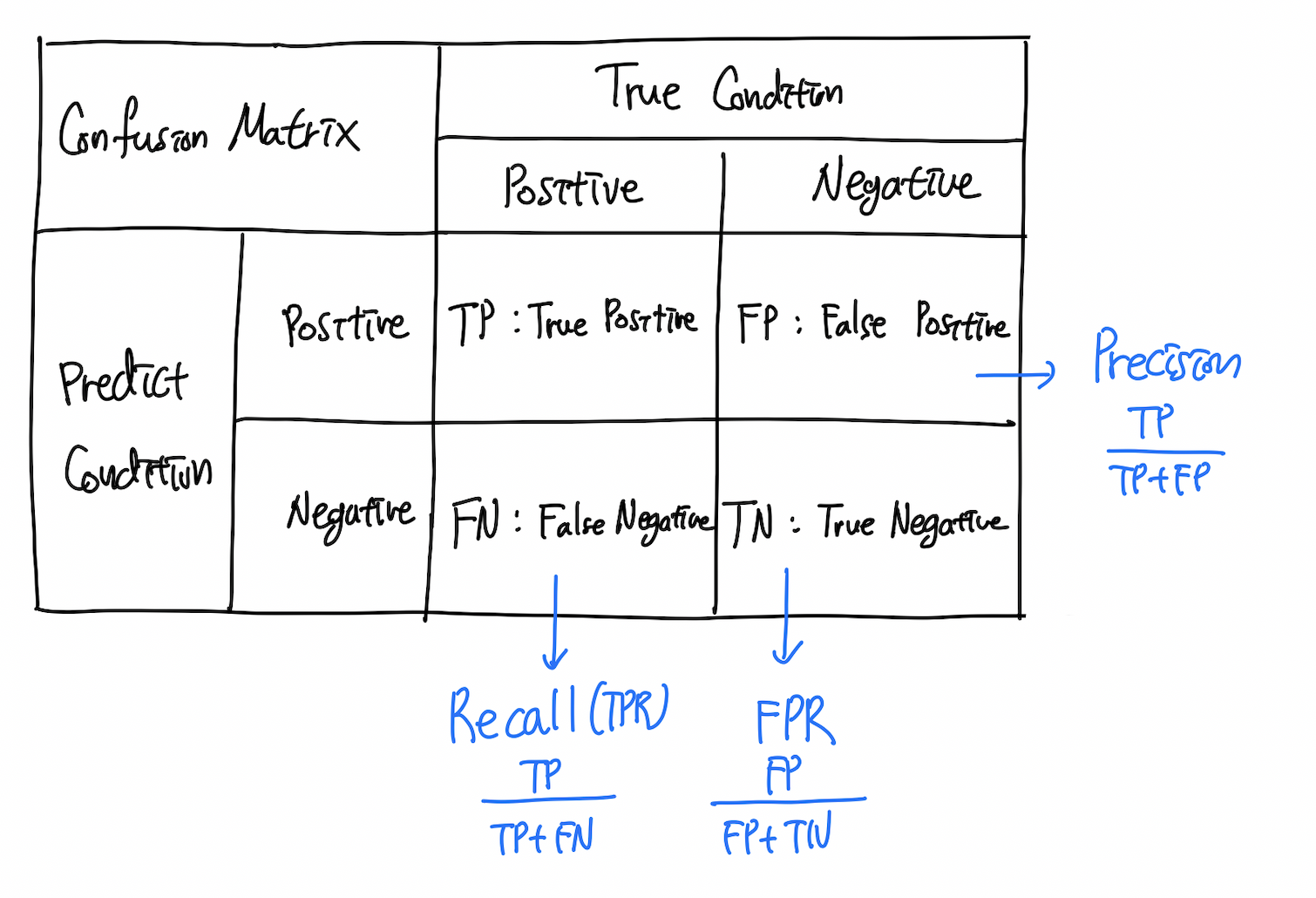
Matric

TP / TN / FP / FN을 사용하여 현재 예측 모델이 얼마나 정확한지 수치화할 수 있다.

Accuracy

어떤 모델의 성능을 판단한다고 할 때 가장 쉽게 떠오르는 것이 있다면 정확도(Accuray)일텐데, 정확도는 다음과 같이 표현할 수 있다.

\[Accuracy = {TP + TN \over TP + TN + FP + FN}\]

정확도는 전체 예측 중 옳은 예측의 비율을 나타내는 것으로, Positive, Negative 각각에 대해 옳은 예측을 의미하는 TP, TN이 분자에 있는 것을 확인할 수 있다.

Precision

Precision은 우리말로 정밀도라고 번역된다.

\[Precision = {TP \over TP + FP}\]

Precision은 Positive로 예측한 것이 얼마나 정확한지에 대해 관심을 가진다. 즉 Positive에 대한 정밀도인 것이다. 구하는 식 또한 Positive로 예측한 경우에서 실제 Positive인 경우의 비율로 표현된다.

Recall(TPR)

\[Recall = {TP \over TP + FN}\]

Recall은 Precision과는 반대로 실제 Positive 중에서 모델이 Positive로 에측한 비율을 의미힌다. 즉, 실제 Positive에 대해 모델이 얼마나 잘 재현하는가에 대한 지표라고 할 수 있다. Recall은 True Positive Rate, 줄여서 TPR이라고도 불린다.

False Positive Rate(FPR)

\[FPR = {FP \over FP + TN}\]

FPR은 False Positive의 비율로, Recall과는 달리 실제 Negative 중 모델이 Negative로 판정한 비율을 의미한다.

ROC curve

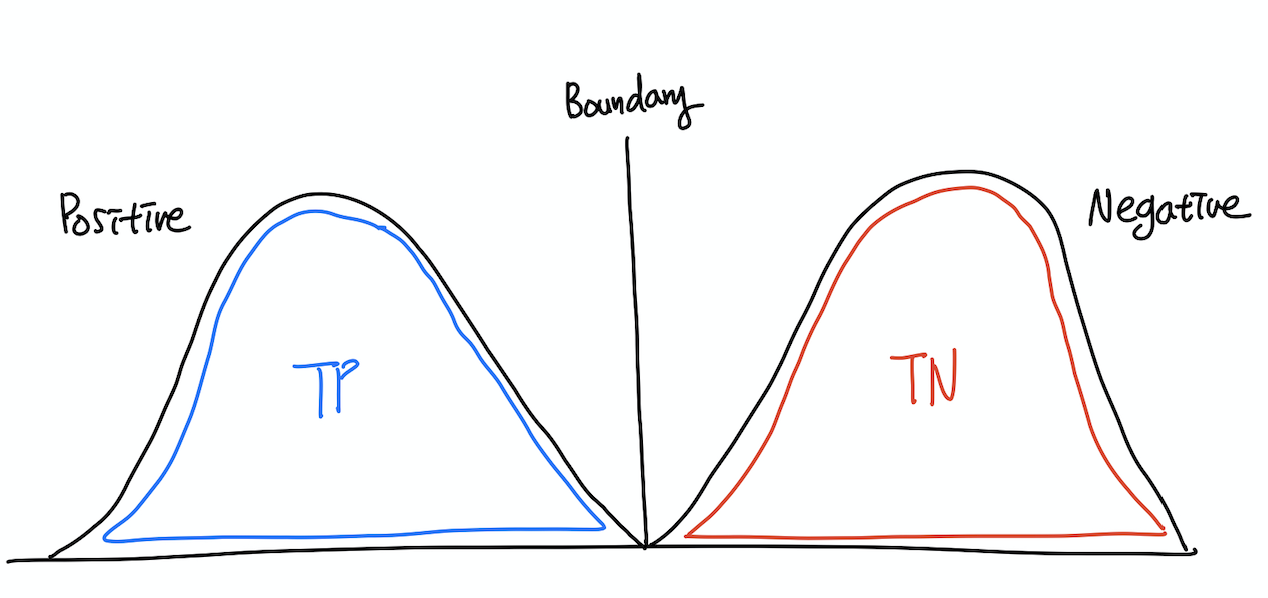
ROC curve는 Receiver-Operating Characteristic curve의 줄임말로, x축으로 FPR, y축으로 TPR을 갖는 평면 위에서 그려지는 curve이다. 직관적으로는 어떻게 그려질지 쉽게 떠오르지 않는데, 결정 경계를 그려보면 보다 쉽게 이해할 수 있다.

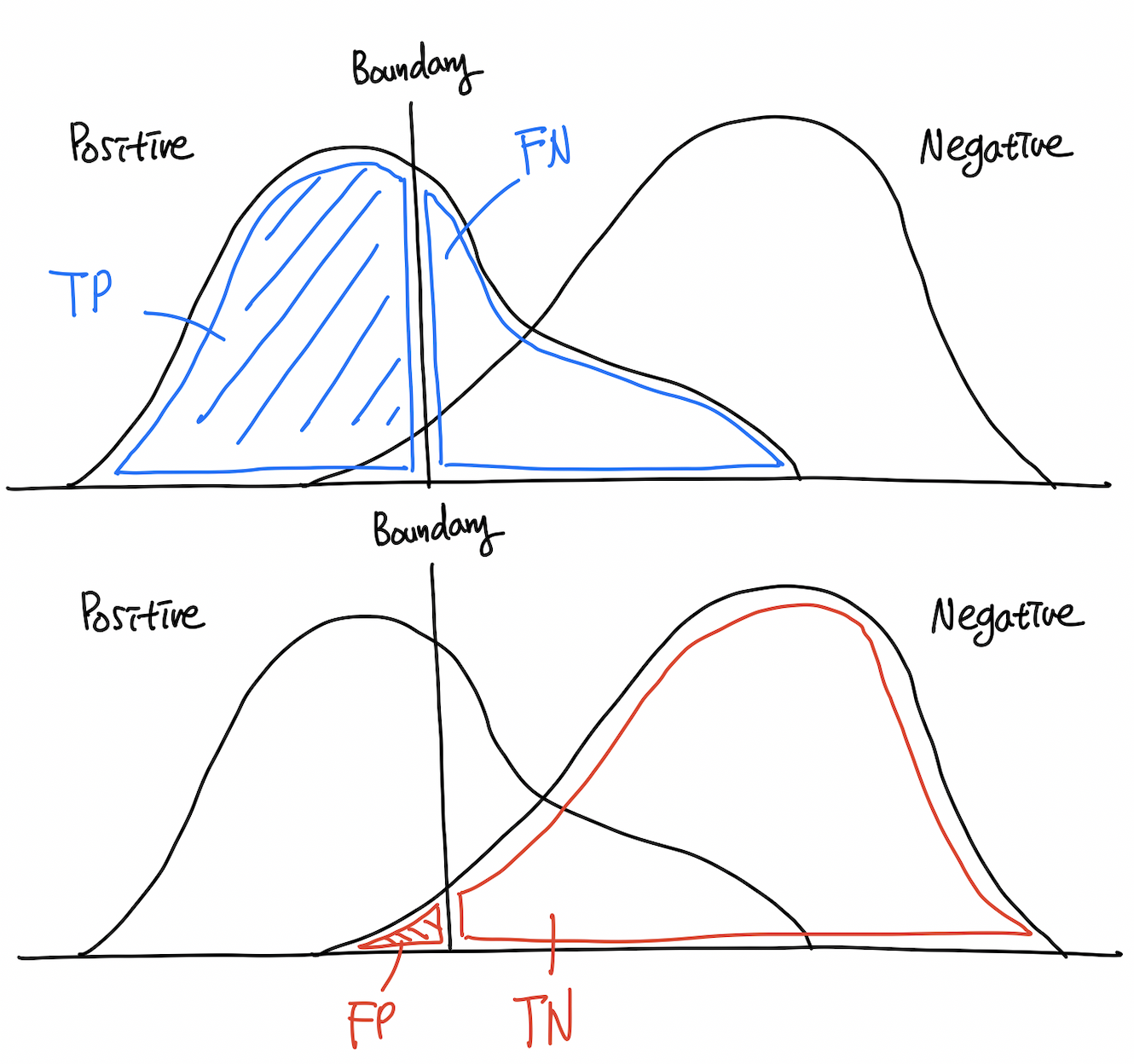
위의 그림에서 파란색으로 표시된 TP + FN의 합은 Positive일 확률의 총합이므로 1이라는 것을 알 수 있고, 그 중 TP가 차지하는 비중은 decision boundary가 오른쪽으로 옮겨감에 따라 커질 것이라는 것도 추측할 수 있다. 빨간 색으로 표시된 FP + TN의 영역 또한 합은 1이고, FP가 차지하는 비중도 decision boundary가 오른쪽으로 옮겨가면서 점점 커지게 된다.

여기서 결정 경계의 움직임에 따라 TPR, FPR이 같은 방향으로 증가, 감소한다는 것을 알 수 있다. 이러한 특성을 이용해 ROC 공간(FPR, TPR) 상에 우상향하는 곡선을 그릴 수 있게 되는데 이것이 바로 ROC curve이다. 즉, ROC curve는 x축 상의 decision boundary를 움직여감에 따라 TP, FP의 상대적인 크기 변화 및 그 관계를 표현하는 그래프라고 할 수 있다.

예를 들어 위의 그림에서 TP가 0.5, FP가 0.05라고 하자.

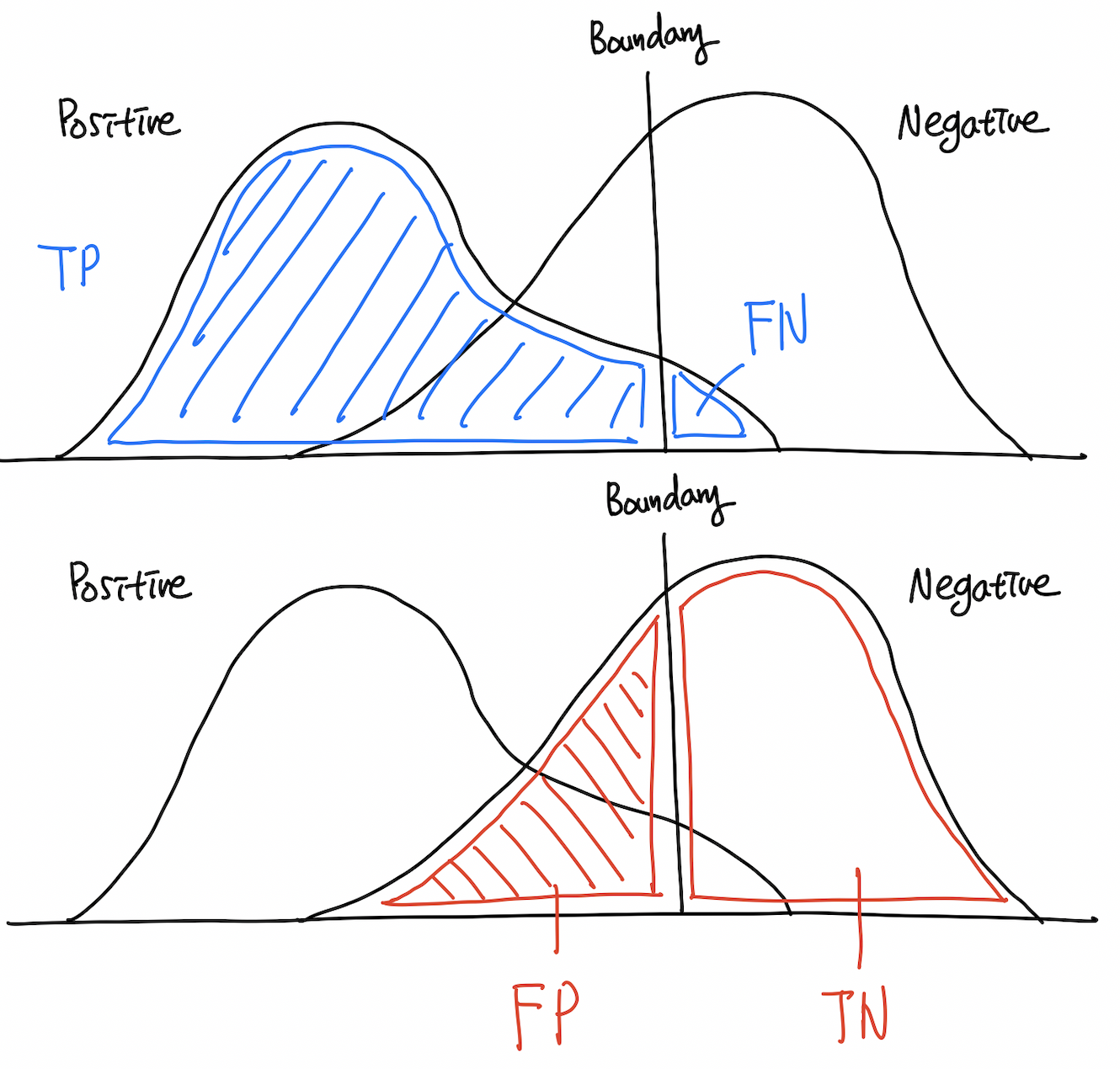
그리고 decision boundary를 오른쪽으로 옮겨 새로 측정해보니 TP가 0.9, FP가 0.4까지 늘었다고 가정하자. 이 경우 ROC 평면 상에는 아래의 왼쪽 그림과 같이 두 개의 점을 찍을 수 있다. 무수히 많은 x에 대해 decision boundary를 상정하고 점을 찍어 이으면 오른쪽 그림처럼 curve를 구할 수 있는데 이것이 바로 ROC curve가 된다.

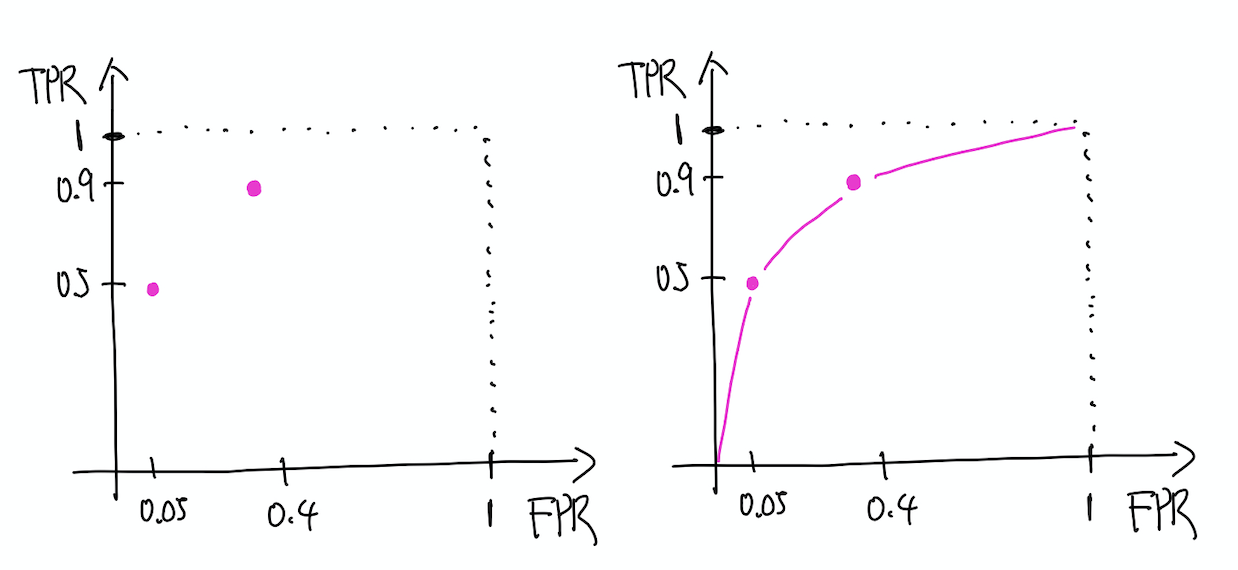
참고로 연속확률공간에서 x의 경우의 수는 무한하므로, 무수히 많은 x에 대해서 구할 수는 없고 test set에 포함된 sample의 수에 대해서만 구하는 것이 일반적이다.

ROC curve가 가장 극단적인 경우는 어떻게 될까. 다시 말해 완벽한 모델을 상정하여 정확도가 100%인 경우라면 다음과 같이 표현할 수 있다.

이같이 Positive, Negative를 완벽하게 나눌 수 있다면, ROC 평면 상의 그래프는 (0,0), (0,1), (1,1)을 직선으로 잇는 형태가 된다.

AUROC

AUROC는 ROC curve로 확인할 수 있는 모델의 성능을 수치화한 것이다. Area Under ROC curve의 줄임말인 AUROC는 말 그대로 ROC curve에 대해 [0,1] 범위에서 적분한 값이다. 바로 위에서 이상적인 경우로 산정한 예에서는 AUROC가 1이 된다. 그리고 랜덤 샘플링의 경우에는 0.5가 된다.

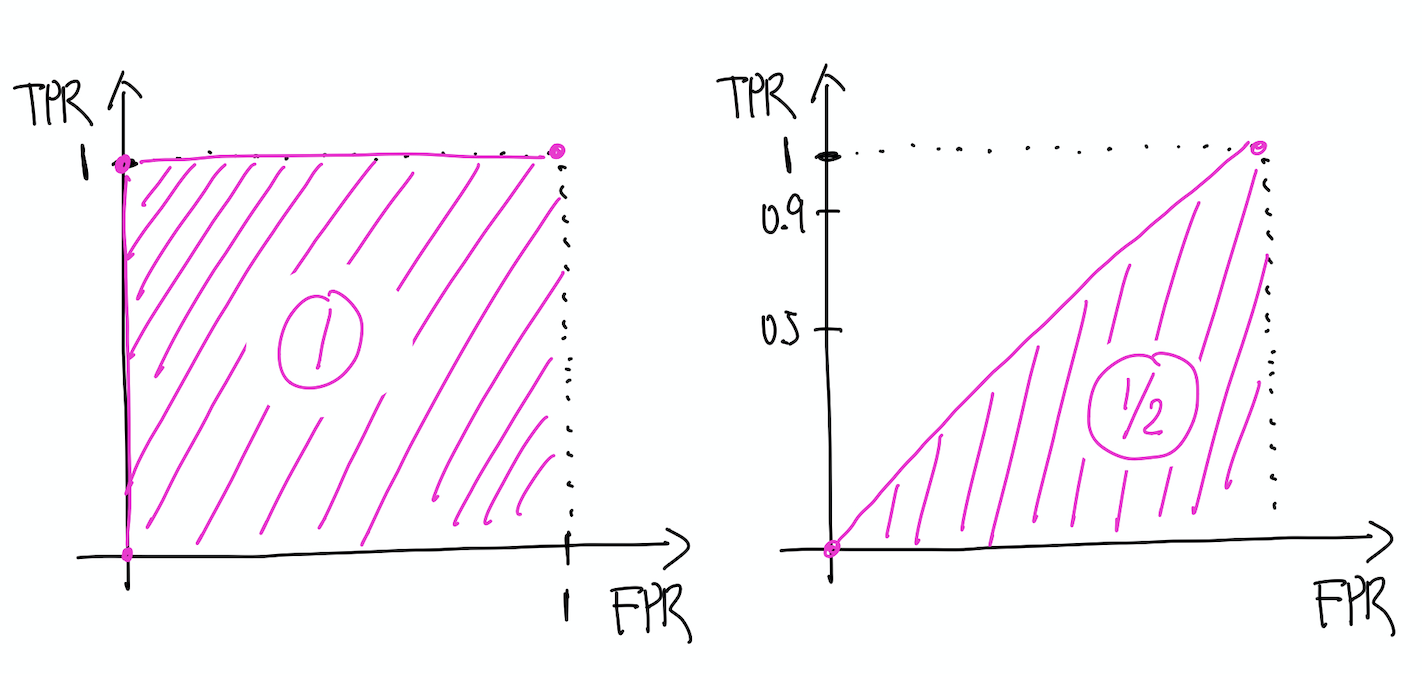
왼쪽이 완벽한 경우, 오른쪽이 랜덤 샘플링의 경우이다.