Decision Theory
- Christopher M. Bishop의 Pattern Recognition and Machine Learning을 참고하여 작성했습니다.
- update date : 2020.02.07
Classification
머신러닝에서 분류 문제란 어떤 주어진 값을 알맞는 클래스로 구분짓는 것이다. 즉 training set에 담겨있는 정보를 통해 분류의 기준을 세워 이후 새로운 정보 \(x\) 각각에 대해 정확한 클래스를 지정해주는 것이다.
분류 문제의 불확실성은 결합 확률 분포 \(P(X, t)\)로 표현할 수 있다. 예를 들어 \(P(X=x_i, t=1)\)는 \(x_i\)이면서 \(t=1\)일 확률을 의미한다. 이때 training set을 이용하여 \(P(X, t)\)를 결정하는 것은 추론(inference) 문제가 된다.
Bayes’ theorem in Disgnosis problem
분류 문제의 대표적인 예시로 진단 문제가 있는데, 이는 X-ray 사진 \(x\)가 있을 때 암세포가 있는지 없는지 정확하게 구분하는 것이다.
- present of cancer : class \(C_1\)
- absence of cancer : class \(C_2\)
통계적으로는 \(P(C_k \lvert x)\)로 표현된다. 즉 어떤 사진 \(x\)가 주어졌을 때 암세포가 있다고 판단할 확률은 \(P(C_1 \lvert x)\)이 되고, 없다고 판단할 확률 \(P(C_2 \lvert x)\)이 된다고 할 수 있다. 이와 같은 조건부 확률은 베이즈 정리에 따라 다음과 같은 등식이 성립한다.
\[P(C_k \lvert x) = {P(x \lvert C_k)P(C_k) \over P(x)}\]위의 식에서 \(P(C_k)\)는 클래스 \(C_k\)에 대한 사전 확률 분포이고, \(P(x \lvert C_k)\)는 가능도(likelihood)이다. 그리고 \(P(C_k \lvert x)\)는 사후 확률 분포가 된다. 즉, 어떤 사진 \(x\)에 암세포가 있다고 판단할 확률은 사전 확률과 가능도의 곱에 비례한다고 할 수 있다.
Decision boundary
분류 문제를 확률 변수 \(X\)의 가능한 값 각각에 대해 정확한 클래스를 찾는 것으로 본다면, 전체 확률 변수 영역 내에서 어떤 영역에 존재하는 샘플에 대해서는 클래스 1로 분류하고, 그렇지 않은 경우에는 클래스 2로 분류하는 것으로 볼 수 있다. 이때 두 영역 간의 경계, 즉 안쪽에 포함되면 클래스 1이 되고 바깥쪽에 포함되면 클래스 2가 되는 경계를 결정 경계(decision boundary)라고 한다.
결정 경계는 새로운 샘플이 들어왔을 때 어떤 클래스로 분류할지 결정하는 기준이 된다. 그리고 분류 문제를 해결하기 위해 모델을 학습한다는 것은 결정 경계를 조정해나가는 것이 된다.
결정 경계와 분류의 정확성
클래스 \(C_1\)로 분류되는 영역을 \(R_1\), \(C_2\)로 분류되는 영역을 \(R_2\)라고 한다면 정확히 분류할 확률은 다음과 같이 표현이 가능하다.
\[\eqalign{ P(correct) &= \Sigma_{k+1}^K P(X \in R_k, C_k)\\ &= \Sigma_{k=1}^K \int_{R_k} P(X, C_k) dX }\]이때 \(P(X, C_k) = P(C_k \lvert X)P(X)\)가 성립하고, P(X)는 데이터의 분포이기 때문에 클래스에 따라 변화하지 않는다. 이러한 점에서 각 \(x\)를 사후분포 \(P(C_k \lvert x)\)가 가장 큰 \(C_k\)로 분류하면 정확하게 분류할 확률이 커진다고 할 수 있다.
반면 잘못 분류할 확률을 다음과 같이 표현할 수 있으며, 우리의 목표는 이것이 최소화되는 것이다.
\[\eqalign{ P(mistake) &= P(X \in R_1, C_2) + P(X \in R_2, C_1) \\ &= \int_{R_1} P(X, C_2) dX + \int_{R_2} P(X, C_1) dX }\]오분류의 가능성은 아래와 같이 그림으로 표현할 수도 있다.
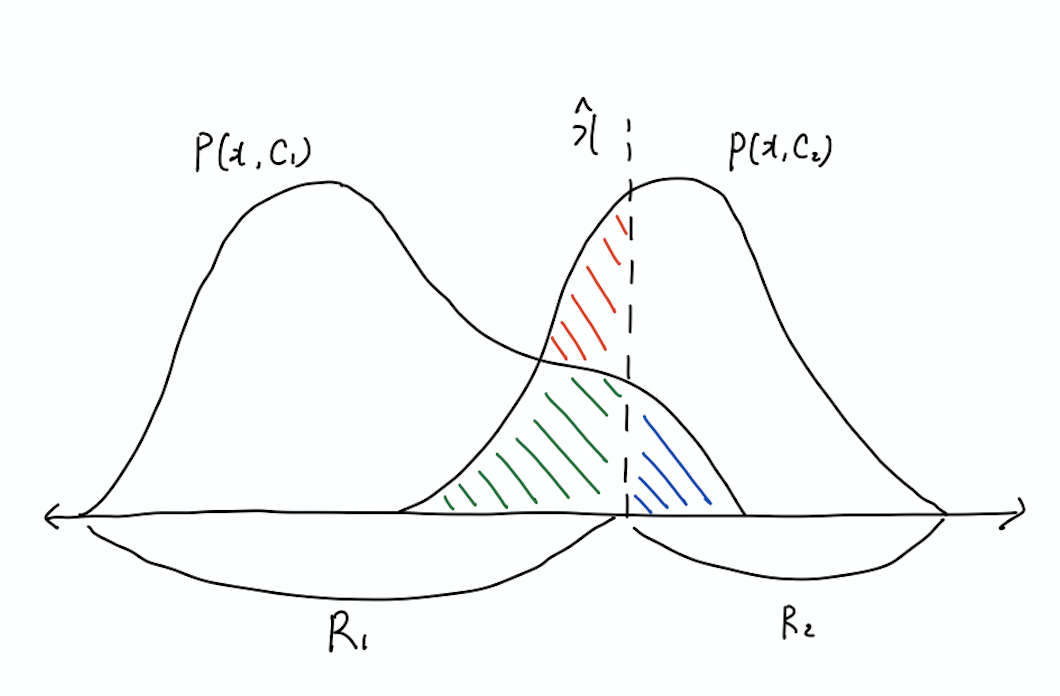
위의 그림에서 \(P(x, C_1)\)은 \(x\)가 \(C_1\)일 확률을, \(P(x, C_2)\)는 \(C_2\)일 확률을 뜻한다. 그리고 \(\hat x\)는 현재의 결정 경계로, 왼쪽은 \(C_1\)로, 오른쪽은 \(C_2\)로 분류되는 영역이 된다. 그런데 위의 그림과 같이 결정 경계를 설정하면 잘못 분류하는 경우가 생기게 된다. 구체적으로는 빨간색과 초록색의 크기의 합만큼 원래 \(C_2\)인 것을 \(C_1\)으로 잘못 분류하게 되고 반대로 파란색의 크기만큼 \(C_1\)를 \(C_2\)로 분류하게 된다.
- \(C_1\)을 \(C_2\)로 오분류 : 파란색
- \(C_2\)을 \(C_1\)로 오분류 : 빨간색 + 초록색
최적의 결정 경계
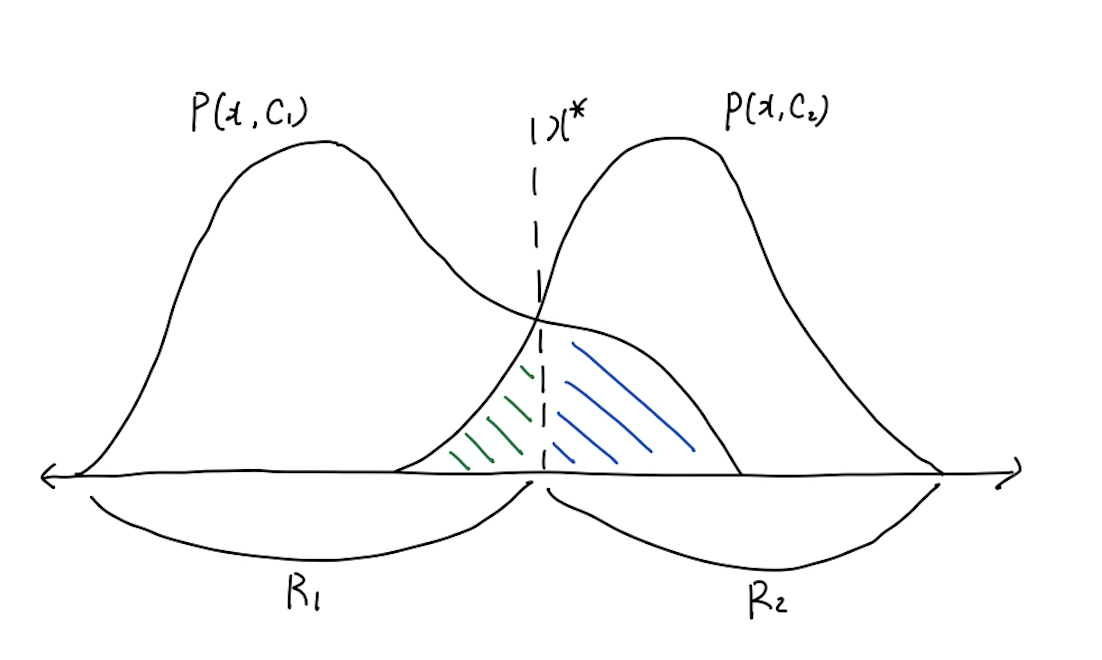
이러한 점을 고려할 때 최적의(optimal) 결정 경계는 위의 그림과 같이 두 확률 함수 \(P(x, C_1)\), \(P(x, C_2)\)가 교차하는 지점이 된다. 이 경우 파란색과 초록색의 크기 만큼은 여전히 오분류가 발생하게 되지만 빨간색 영역 만큼은 줄어들게 된다.
- \(C_1\)을 \(C_2\)로 오분류 : 파란색
- \(C_2\)을 \(C_1\)로 오분류 : 초록색
3 kind of classification methods
분류 문제를 해결하는 데에는 구체적으로 generative model, discriminative model, discriminant function 세 가지 방법이 있다. 앞의 두 가지는 확률을 통해 추정하는 것이고, discriminant function은 직접적으로 분류하는 함수를 찾는 방법이다.
1) Generative model
개별 클래스에 대한 class-conditional density와 prior를 통해 문제를 해결하는 방법이다. 이때 베이즈 정리를 이용하면 posterior를 구할 수 있고, marginalize를 통해 \(p(x)\)를 구할 수도 있다.
\[\eqalign{ &p(C_k \lvert x) = {p(x \lvert C_k) p(C_k) \over p(x)}\\ &p(x) = \Sigma_k p(x |C_k) p(C_k) }\]이 경우 추론의 결과로 얻은 모델을 통해 있을 법한 새로운 데이터를 만들어낼 수도 있다. 이러한 점에서 generative model이라고 한다. 물론 생성한 모델의 성능이 좋지 않다면 새롭게 구한 데이터 또한 좋지 못할 것이다.
- 장점: \(p(x)\)를 구할 수 있기 때문에 각 입력값이 그럴싸한 정도를 확인할 수 있다. 이러한 점 때문에 이상치 탐지에 강점을 보인다.
- 단점: \(x\)와 \(C_k\)의 결합 확률 분포 \(p(x, C_k)\)를 다루는데, \(x\)의 차원이 큰 경우에는 연산 비용이 많이 소요된다. 또한 데이터에 따라 적용하기 어려울 수 있다.
2) Discriminative model
posterior \(p(C_k \lvert x)\)를 직접 근사하는 방법이다. class-conditional density에 비해 posterior가 단순할 수도 있는데, 이러한 경우 사용한다.
- 장점: generative model에 비해 비용이 덜 든다.
3) Discriminant function
어떤 입력 \(x\)에 대해 적절한 class를 반환하는 함수를 직접 구하는 방법이다.
- 장점: 가장 단순한 방법이다.
- 단점: posterior를 구할 수 없다.
구체적으로 posterior를 구할 수 없다는 점은 다음과 같은 한계를 갖는다.
- 일정 수준 이하의 posterior를 갖는 값에 대해서는 판별을 유보할 수 있는데, posterior를 구할 수 없으면 이러한 방법을 사용하기 어렵다.
-
클래스 불균형 문제가 있을 때 인위적으로 균형을 맞춘 데이터를 학습하게 되는데, posterior를 통해 원 데이터 분포를 파악할 수 있다.
\[p(y=c|x) = \frac {p(y=c)q(y=c \lvert x) \over q(y=c)} {\Sigma_{c'} {p(y=c')q(y=c' \lvert x) \over q(y=c')}}\]- 위 식에서 \(p(y=c)\)는 원 데이터셋에서의 prior를, \(q(y=c)\)는 균형을 맞춘 데이터셋의 prior를 의미한다.
Loss function
손실 함수(loss function) 또는 비용 함수(cost function)는 잘못 분류한 경우 발생하는 손실과 관련된 함수이다. 즉 \(C_1\)을 \(C_2\)로 분류했을 때보다 \(C_2\)를 \(C_1\)으로 분류하는 것이 보다 심각한 문제를 초래하는 경우가 있는데, 이러한 점을 고려하여 오분류의 절대적인 크기가 아닌 오분류로 인한 손실의 크기를 표현하는 것이 손실 함수이다. 그리고 이러한 손실 함수의 크기를 최소화하는 것이 목표가 된다.
정답 클래스가 \(C_k\), 모델에 의해 선택된 클래스가 \(C_j\)인 어떤 샘플 \(x\)가 있다고 하자. 그리고 잘못 선택하였을 때 발생하는 손실을 \(L_{kj}\)라고 하면, 전체 손실함수의 기대값은 다음과 같이 표현할 수 있다.
\[E[L] = \Sigma_k \Sigma_j \int_{R_j} L_{kj}P(X, C_k) dX\]그리고 K = {1,2}, J = {1,2} 를 가정하면 위 식은 다음과 같이 풀어쓸 수 있다.
\[\eqalign{ E[L] &= \int_{R_1} L_{11}P(X, C_1) dX \\ &+ \int_{R_1} L_{21}P(X, C_2) dX \\ &+ \int_{R_2} L_{12}P(X, C_1) dX \\ &+ \int_{R_2} L_{22}P(X, C_2) dX }\]각각의 샘플 \(x\)는 어떤 클래스 \(C_j\)로 분류되는데, 매 경우 손실의 크기가 최소가 되도록 해야 한다. 이때 \(L_{11}\)과 \(L_{22}\)의 경우 정확하게 맞춘 것이 되므로 0이라 한다면,
\[\eqalign{ E[L] &= \int_{R_1} L_{21}P(X, C_2) dX \\ &+ \int_{R_2} L_{12}P(X, C_1) dX }\]이 성립한다. \(R_1\)의 범위에서 \(C_2\)로 분류될 가능성과 \(R_2\)의 범위에서 \(C_1\)로 분류될 가능성을 최소화하되 이때 두 가지 loss \(L_{21}, L_{21}\)를 적절히 고려하여야 한다는 것으로 이해할 수 있다.
참고로 \(L_{11}, L_{22}\)와 같이 예측값과 정답이 동일하면 0, \(L_{21}, L_{12}\)와 같이 틀리면 1의 손실을 가정하면 일반적인 분류 문제와 동일해진다. 이를 0/1 loss라고도 한다.
Loss functions for Regression
회귀 문제의 목표는 target value \(t\)에 가까운 \(y(x)\)를 선택하여 기대 손실 함수를 최소화하는 것이다. 데이터셋 \(X = {x_1, x_2 ... x_n}\)에 대한 기대 손실 함수\(E[L]\)은 다음과 같이 정의된다.
\[E[L] = \int \int L(t, y(x))p(x, t) dx dt\]여기서 손실함수를 \(L(t, y(x)) = \{ y(x) - t \}^2\) 로 정의하면 기대 손실 함수는 다음과 같다.
\[E[L] = \int \int \{ y(x) - t \}^2p(x, t) dx dt\]이를 전체 데이터 셋이 아닌 개별 \(x\)에 대한 식으로 바꾸면 다음과 같다.
\[E[L] = \int \{ y(x) - t \}^2p(x, t) dt\]위 식을 최소화하기 위해서는 \(y(x)\)에 대해 미분했을 때 그 값이 0이 되는 지점을 찾아야 한다.
\[{\delta E[L] \over \delta y(x)} = 2 \int (y(x) - t) p(t, x) dt = 0\]전개하면 다음과 같다.
\[\eqalign{ &\int (y(x) - t) p(t, x) dt = 0 \\ &\Rightarrow \int y(x) p(t, x) dt = \int t p(t, x) dt \\ &\Rightarrow {\int y(x) p(t, x) dt \over p(x)} = {\int t p(t, x) dt \over p(x)} \\ &\Rightarrow \int y(x) p(t \lvert x) dt = \int t p(t \lvert x) dt \\ &\Rightarrow y(x)= \int t p(t \lvert x) dt = E[t \lvert x] }\]