On-Policy Approximation of Action Values

• Sutton의 2011년 책 Reinforcement Learning: An Introduction 2nd edition을 참고해 작성했습니다.

Introduction

10x10 Grid World와 같이 State와 Action의 개수가 적어 Table의 형태로 모든 State 혹은 State Action pair에 대한 Value를 저장해 두고 하나씩 업데이트하는 것이 가능한 경우를 Tabular RL Problem이라고 한다. 하지만 많은 문제, 특히 현실에 가까워질수록 State와 Action의 개수가 크게 많아지면서 모든 경우의 수에 대해 Table의 형태로 저장하는 것이 어려워진다. 이는 저장 공간(Memory)의 문제와 더불어 각각의 State 또는 State-Action Pair에 대해 개별적으로 Value를 업데이트해줘야 하기 때문에 연산량이 크게 늘어난다는 문제로 이어진다.

이러한 문제를 해결하기 위해서는 일반화 효과(Generalization), 즉 소수의 State에 대해서만 Policy가 업데이트 되었을지라도 경험하지 못한 State에서도 당황하지 않고 적절한 Action을 선택할 수 있도록 해야 한다. 특히 현실적으로 모든 State를 경험하고 이를 학습한다는 것이 불가능할 만큼 State Space가 큰 상황이 많다는 점을 고려한다면 이러한 일반화 효과의 필요성은 더욱 중요해진다.

Function Approximation

여기서 말하는 일반화 효과는 목표로 하는 어떤 이상적인 Function이 존재하고, 이를 근사한다는 점에서 지도학습(Supervised Learning)의 개념인 Function Approximation과 동일하다고 할 수 있다. 따라서 지도학습에서 Function Approximation을 위해 사용되는 인공신경망, 의사결정트리 등과 같은 방법론들을 강화학습에도 도입하여 이러한 일반화 효과를 얻을 수 있다. 다만 지도학습은 학습에 사용되는 데이터셋이 확정되어있다면 강화학습은 Policy의 업데이트에 따라 환경과의 상호작용의 결과가 바뀌고 그에 맞춰 학습의 대상이 되는 데이터의 분포가 변화할 수 있다는 점에서 강화학습에 사용되는 방법론은 지속적으로 늘어나는 데이터 및 변화하는 데이터의 분포에 유연하게 대처할 수 있어야 한다.

Approximating Value Function

Value Function을 근사한다는 것은 현재 Policy \(\pi\)가 주어져 있을 때, 이에 대한 정확한 Value Function인 \(v_\pi(s)\)를 Parameterized Funciton \(\hat v_\pi(s, \boldsymbol{w})\)으로 근사하겠다는 것을 의미한다.

\[\hat v_\pi(s, \boldsymbol{w}) \approx v_\pi(s)\]

지도학습에서는 어떤 입력이 주어졌을 때 입력에 맞는 Label을 출력으로 나오도록 학습이 이뤄진다. 강화학습의 Value Function을 근사하는 것이 목표라면 State라는 입력이 주어졌을 때 State Value라는 Label이 나오도록 해야 한다. 이때 이 Label을 어떻게 구할 것인가에 따라 강화학습의 여러가지 방법론들이 나누어진다고 할 수 있다. 만약 state \(s\)의 state value를 \(v\)로 보고 업데이트한다고 할 때 그 표기법은 다음과 같다.

\[s \mapsto v\]

즉 왼쪽에 입력인 state \(s\)가 주어지고, State에 대한 Value Function Approximation 값이 오른쪽의 \(v\)에 보다 가까워지도록 업데이트하겠다는 것으로 보고 아래 식을 이해하면 된다.

RL Method	Backup Operation
Monte Carlo(MC)	\(S_t \mapsto G_t\)
Temporal Difference TD(0)	\(S_t \mapsto R_{t+1} + \gamma \hat v(S_{t+1}, w_t)\)
Temporal Difference TD(\(\lambda\))	\(S_t \mapsto G_t^\lambda\)
Dynamic Programming(DP)	\(S_t \mapsto E_\pi[R_{t+1} + \gamma \hat v (S_{t+1}, w_t) \lvert S_t = s]\)

한 가지 덧붙이자면 일반화 효과를 거두기 위해서는 전체 State의 개수보다 근사 함수의 Parameter 개수\(\lvert \boldsymbol{w} \rvert\)가 적어야 한다. 이는 곧 하나의 \(w\)를 업데이트하면 복수의 state에 대한 값이 업데이트된다는 것을 의미한다.

Performance Measure for Approximation

어떤 함수를 근사한다고 한다면 얼마나 근사를 잘했는지 평가할 수도 있어야 할 것이다. 지도학습의 방법론을 사용하는 만큼 그것에 대한 평가 척도도 지도학습의 것을 그대로 사용할 수 있는데, 평균 제곱근 오차(root-mean-squared error, RMSE)가 대표적이다.

\[\text{RMSE}(w) = \root \of { \Sigma_{s \in \mathcal S} d(s) [v_\pi(s) - \hat v (s, w)]^2 }\]

평균 제곱근 오차는 워낙 많이 사용되는 것이므로 특별할 것 없지만 \(d(s)\)가 곱해지면서 단순 평균이 아니라 가중 평균이라는 점에 유의할 필요가 있다. \(d(s)\)는 State에 따른 중요도를 의미한다는 점에서 어떤 State에서는 Value 계산에 오차가 어느 정도 있어도 되지만, 중요한 State에 대해 발생하는 Value 오차는 보다 크게 줄여야 한다는 것으로도 이해할 수 있다.

이와 같이 State 별로 가중치를 두고 오차를 계산하는 것은 Parameter의 개수가 State의 개수보다 적어 현실적으로 모든 State에서의 Error를 0으로 만드는 것이 많은 경우 불가능하기 때문이다. 오차가 0이 되는 해가 존재하지 않는 상황이므로 오차를 최소한으로 줄이는 방향으로 업데이트해야 하고, 따라서 중요한 State에 대해서는 오차를 크게 줄이도록 하는 것이 성능에 큰 영향을 미칠 수 있다.

On-Policy Distribution

그렇다면 State 간의 상대적인 중요도를 정할 필요가 있다. 가장 먼저 생각나는 방법은 Value Function이 어떤 Policy \(\pi\)에 대한 것인 만큼 현재 Poilcy \(\pi\)에 따라 Agent가 Action을 수행할 때 State를 방문하는 빈도가 크면 클수록 중요한 State로 보는 방법이다. 많이 방문하는 State에서 정확히 판단하는 것이 중요하다는 점에서 그 오차에 민감하게 반응하도록 하는 것이 직관적이기도 하다. 이와 같이 현재 Policy에 따라 Action을 결정할 때 State의 방문 빈도를 On-Policy Distribution이라고 한다.

Gradient Descent Method

Function Approximation Method의 대표적인 방법론이 딥러닝과 함께 너무나도 유명해진 Gradient Descent Method이다. Gradient Descent Method에 대해 매우 간단하게 정리하면, 기본적으로 다음과 같은 column vector로 이뤄진 parameter \(\boldsymbol{w}\)를

\[\boldsymbol{w} = (w_1, w_2, ... w_n)^T\]

목적함수(여기서는 RMSE)의 Gradient \(\nabla f(w_t)\)에 따라 업데이트하는 방법이다.

\[\eqalign{ \boldsymbol{w_{t+1}} &= \boldsymbol{w_{t}} - {1 \over 2} \alpha \nabla [v_\pi(S_t) - \hat v(S_t, \boldsymbol{w_t})]^2\\ &= \boldsymbol{w_{t}} \alpha [v_\pi(S_t) - \hat v(S_t, \boldsymbol{w_t})] \nabla \hat v (S_t, \boldsymbol{w_t}) }\]

여기서 \(\alpha\)는 Step Size이고, Gradient \(\nabla f(w_t)\)는 개별 파라미터의 편미분으로 구해진다. 업데이트가 진행됨에 딸 Step Size는 점차 줄어드는 것이 일반적인데, 이것이 Stochastic Approximation Theorem을 만족하면 Local Optimum으로의 수렴이 보장된다(CHAPTER 2. MULTI-ARM BANDITS).

\[\Sigma_{k=1}^\infty \alpha_k(a) = \infty \qquad \text{and} \qquad \Sigma_{1}^\infty \alpha^2_k(a) < \infty\]

Step Size외에도 Value Function Approximation의 수렴성이 보장되기 위해서는 학습에 사용되는 State Value \(V_t\)에 Bias가 존재해선 안 된다는 조건이 붙는다. 즉 아래의 식을 만족해야 한다.

\[E[V_t] = v_\pi(S_t)\]

이것의 대표적인 예시가 Monte Carlo Method인데, Monte Carlo에서는 어떤 State의 Value를 실제로 수행한 Episode에서 구한 Return \(G_t\)로 상정하기 때문에 Variance는 존재하더라도 Bias는 존재하지 않으므로 위의 식을 만족한다.

Linear Methods

선형 모델(Linear Method)는 Gradient Descent Function Approximation의 특별한 예시 중 하나로 \(\hat v\)를 선형함수로 만드는 것이다. 즉 일반적인 딥러닝 모델과 달리 Non-Linearity가 없는 경우라고 할 수 있다. Non-Linearity가 없으므로 Universal Function Approximation Theorem의 조건을 만족하지 못한다. 하지만 이와 같은 선형 모델은 Optimal \(\boldsymbol{w}^*\)가 단 하나 존재한다는 특성을 가진다. 따라서 Linear Method는 수렴성이 보장되기만 한다면 Local Mimumum에 빠지지 않는다.

\[\hat v (s, \boldsymbol{w}) = \boldsymbol{w}^T x(s) = \Sigma_{i=1}^n w_i x_i(s)\]

위의 식에서 \(x(s)\)는 State의 Feature로 아래 식과 같이 단순하게 구할 수도 있고, 다른 여러 방법들을 사용할 수도 있다.

\[x(s) = (x_1(s), x_2(s), ...x_n(s))^T\]

선형 모델은 위에서 확인한 모든 RL Method들에 대해 On-Policy Distribution을 가정하면 수렴성이 보장된다. 예를 들어 TD(\(\lambda\))는 Step Size가 Stochastic Approximation Theorem를 만족하고 무한히 Parameter를 업데이트한다고 가정하면 다음과 같이 오차가 Bound 된다.

\[RMSE(\boldsymbol{w}_\infty) \leq {1 - \gamma \lambda \over 1 - \gamma} RMSE(\boldsymbol{w}^*)\]

\(RMSE(\boldsymbol{w}^*)\)는 Optimal Parameter에서의 오차이므로 이상치가 되고, \(\lambda\)가 1에 가까워지면 가까워질수록 이상치에 점차 가까워지는 것으로 이해할 수 있다.

Feature as State Representation

선형 모델의 수렴성은 증명이 되었지만 현실적으로 무한히 Parameter를 업데이트 할 수는 없으므로 효율적으로 수렴하도록 하는 방법 또한 중요하다. 선형 모델의 효율적인 업데이트를 위해서는 개별 State를 표현하는 방법, 즉 Feature \(x(s)\)를 잘 설정하여 한 번에 유사한 여러 State에 대한 Value들을 업데이트하는 일반화 효과를 높여야 한다. 다시 말해 좋은 Feature란 일반화 효과를 높일 수 있도록 State 간의 연관성을 포착할 수 있어야 한다.

이러한 점에서 책에서는 강화학습에서의 Domain Knowledge를 강조한다. 환경에 대한 지식을 가지고 그것을 반영하도록 State의 Feature를 뽑아내면 보다 효과적인 업데이트가 가능해지기 때문이다.

Coarse Coding

Feature 설정의 중요성을 보다 구체적으로 확인하기 위한 예시이자 State를 Feature로 표현하는 방법 중 하나로 Coarse Coding이 있다. Coarse Coding이란 State Space를 어떤 특징을 가지는 State들에 대해서는 1, 그렇지 않은 State에 대해서는 0을 부여하는 방법을 말한다. 이러한 점에서 Coarse Coding으로 만들어진 Feature를 Binary Feature라고도 한다. 예를 들어 2차원의 State Space에서 개별 Feature를 다음 원과 같이 표현했다고 하자.

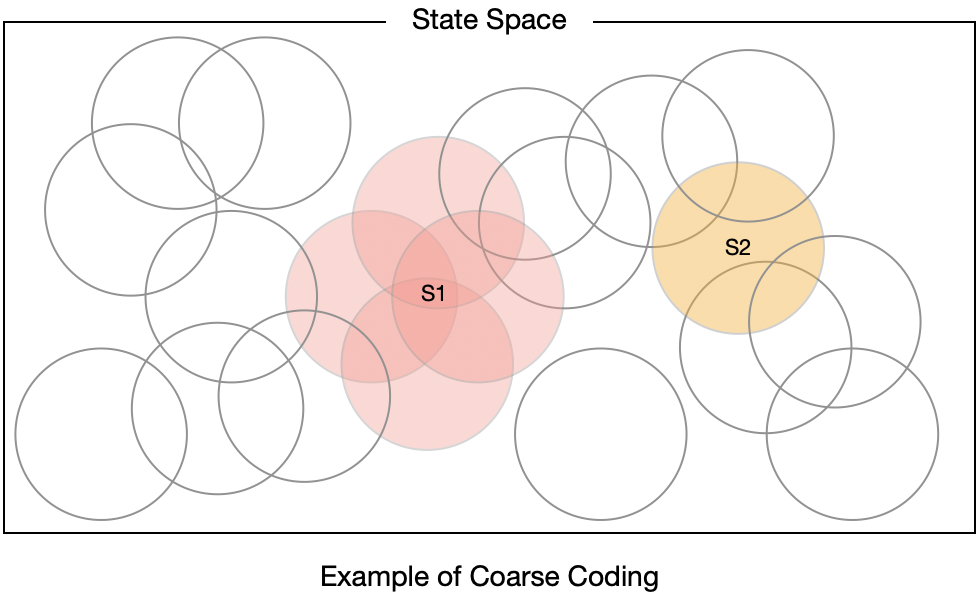
이때 Coarse Coding은 아래 Vector처럼 표현된다. 즉 원 안에 들어가면 1, 그렇지 않으면 0이 부여되는 식이다.

선형 모델을 Gradient Descent 방법으로 근사한다고 가정하면, State Space 상에 표현되어 있는 원은 어떤 State에 대해 학습이 이뤄질 때 업데이트 되는 \(\boldsymbol{w}\)의 개별 파라미터를 의미하는 것으로도 볼 수 있다(Reception Feild). 그렇다면 원의 크기가 크면 클수록 한 번의 업데이트로 보다 많은 State의 Value가 영향을 받는다는 점에서 일반화 효과가 크고, 반대로 작으면 작을수록 일반화효과가 작은 것이 된다. 아래의 두 예시는 차례대로 중심점은 모두 동일하지만 원이 작은 경우와 원이 큰 경우를 보여주고 있다.

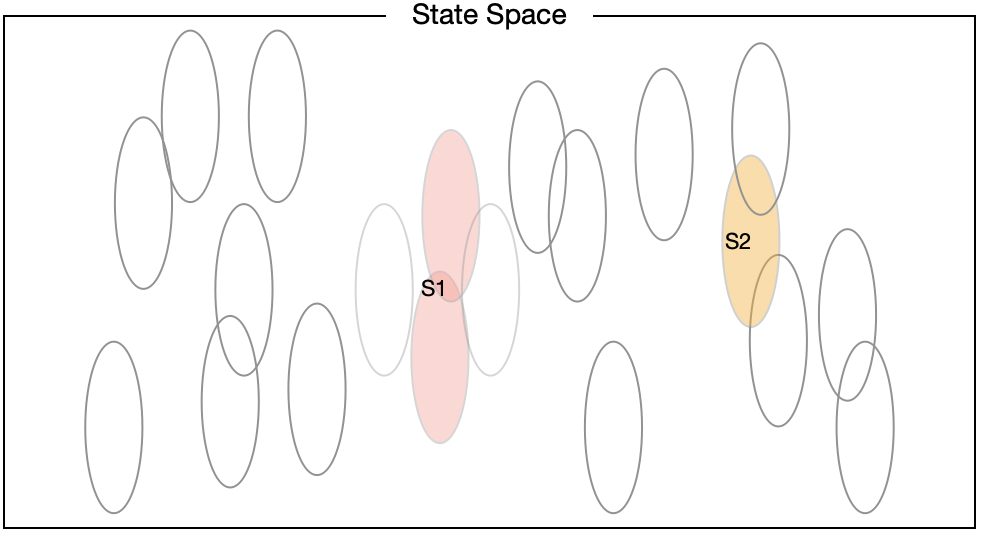
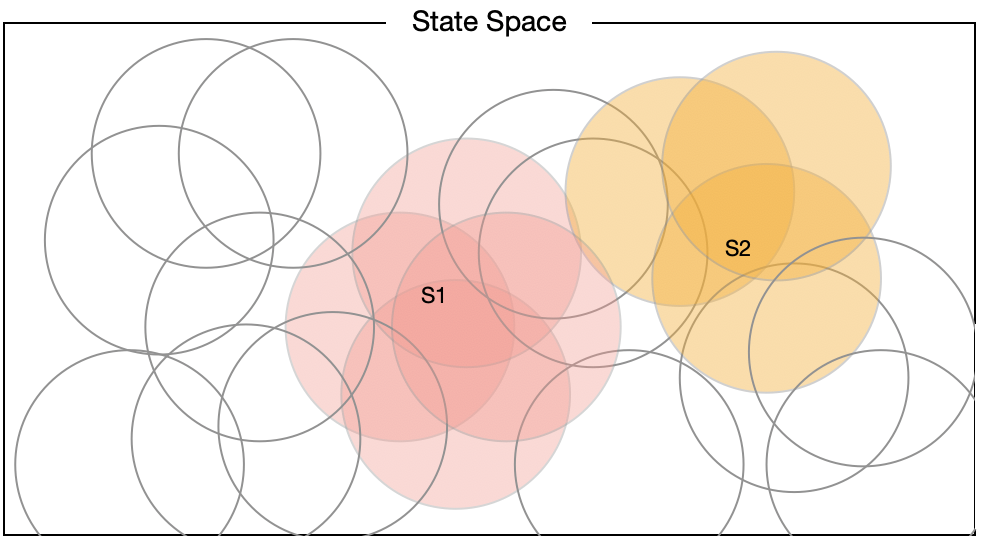
당연한 말이지만 원의 크기가 크면 클수록 State Space 상에서 업데이트가 이뤄지는 영역의 크기가 커진다는 것을 알 수 있다. 즉 Reception Field가 크면 클수록 일반화의 효과가 크다. 위의 그림과 같이 원으로 표현하는 것은 Coding의 예시일 뿐 구체적인 방법은 다양하게 제시될 수 있다. 책에서는 Tile Coding, Radial Basis Functions, Kanerva Coding 등을 예시로 들고 있으며, 어떤 방법을 택하느냐에 따라 Reception Field의 형태는 달라질 수 있다.

Size and Shape of Reception Field

원(Reception Field)의 크기에 따라 Function Approximation이 이뤄지는 양상도 달라지게 진다. 아래 그림은 Feature의 분포 등 다른 조건들은 모두 동일하고 Feature의 크기만 Narrow, Medium, Broad 세 가지로 나누어 Value Function에 수렴한 결과를 보여주고 있다. State Space를 1차원으로 가정하므로 Circle이 아니라 Interval로 표현되며, Square Wave 형태의 Value Function을 근사하는 것을 목표로 한다.

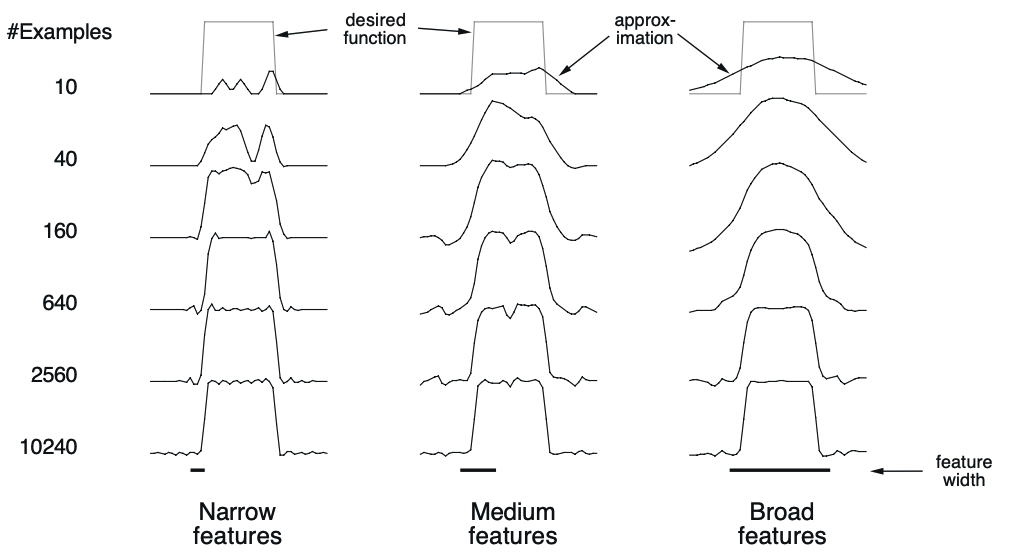
10개의 Example에 대해 학습을 했을 때에는 크게 차이나지만 오랫동안 학습이 이뤄진 후의 결과는 크게 차이가 없다. 즉 Reception Field에 따라 학습의 양상에는 차이가 발생하더라도 Feature의 분포가 적절하다면 거의 동일하게 수렴한다는 것을 확인할 수 있다.

Non-linear Gradient Method

Non-Linear Gradient Method에서는 Backpropagation을 통해 학습이 이뤄진다. 선형 모델에서는 복수의 레이어를 쌓는 것이 의미가 없지만 레이어마다 비선형성이 추가되는 경우에는 그것을 쌓았을 때 입력값에서 보다 복잡한 특성을 포착해낼 수 있게 된다. 따라서 비선형 모델을 사용하면 레이어를 많이 쌓아 Feature를 추출하는 부분을 대신할 수도 있다.

Should we bootstrap?

지금까지 Bootstrapping Method를 중심으로 Function Approximation을 소개했지만 이론적으로는 Non-bootstrapping Method들에 Function Approximation을 적용하는 것이 더욱 안정적인 수렴이 보장된다고 한다. 그럼에도 Bootstrapping Method를 강화학습에서 많이 사용하는 것은 성능이 더 좋기 때문이다. 이에 대해 Sutton은 On-Policy Bootstrapping Method가 더 잘 되는 이유는 불확실(unclear)하고 이에 대해서는 보다 많은 연구가 필요하다고 언급한다.