Dynamic Programming
- Sutton의 2011년 책 Reinforcement Learning: An Introduction 2nd edition을 참고해 작성했습니다.
Summary
- 강화학습에서 Dynamic Programming이란 Optimal Policy를 구하기 위해 각각의 State에 대한 Value를 정확히 구하는 방법을 말한다.
- Policy Iteration은 Value Function을 정확하게 구하는 Policy Evaluation과 새로운 Value Function에 맞춰 보다 나은 Policy를 찾는 Policy Improvement 두 가지로 구성되어 있다.
- Policy Iteration의 비효율성을 해소하기 위해 수렴성을 봊장하면서도 보다 효율적인 Value Iteration, Asynchronous Update 등이 있다.
Introduction
Dynamic Programming(DP)이란 한 번에 해를 구하기 어려운 문제가 있을 때 이를 여러 개의 하위 문제로 분할하고 각각에 대한 해를 찾아 본래의 문제를 해결하는 방법이다. 기본적으로 DP는 본래의 문제를 해결할 수 없거나, 본래의 문제를 곧바로 해결하는 데에 소요되는 비용보다 복수의 하위 문제를 해결하는 데에 소요되는 총 비용이 더 작을 때에 유용하다.
강화학습의 목표는 주어진 환경에 대해 Optimal Policy를 찾는 것이다. 하지만 이를 무턱대고 구하는 것은 쉽지 않기 때문에 각 State 또는 State-Action Pair의 Value를 먼저 구하고 이를 사용하여 Optimal Policy를 구하는 방법을 생각해 볼 수 있다. 즉 강화학습에서의 DP란 각 State에 대한 Value를 구하는 작은 문제를 해결하여 Optimal Policy라는 큰 문제를 해결하는 방법이다.
Policy Iteration
각 State(또는 State-Action Pair)의 Value를 보다 정확하게 계산하는 Value Function을 구하는 방법으로 Bellman Equation이 있었다. 만약 아래와 같이 Bellman Optimality Equation을 만족하는 Optimal Value Function을 찾는다면 그에 따라 Optimal Policy도 구할 수 있다.
\[\eqalign{ v^*(s) &= \max_{a \in A(s)} \Sigma_{s', r} p(s', a \lvert s, a) [r + \gamma v^*(s')]\\ q^*(s, a) &= \Sigma_{s', r} p(s', r \lvert s, a) [r + \gamma \max_{a'} q^*(s',a')] }\]당연하게도 Optimal Value Function을 구하는 것 역시 쉽지 않다. 그런데 현재의 Policy가 갖는 Value Function을 정확히 계산하고, 이를 통해 보다 나은 Policy를 구하는 방법으로 Optimal Value Function과 유사한 Value Function을 구하는 것이 가능하다. Policy Iteration은 Value Function을 정확하게 구하는 Policy Evaluation과 새로운 Value Function에 맞춰 보다 나은 Policy를 찾는 Policy Improvement 두 가지를 통해 Optimal Policy를 구하는 방법이다.
\[\pi_0 \rightarrow^E v_{\pi_0} \rightarrow^I \pi_1 \rightarrow^E v_{\pi_1} \rightarrow^I ... \rightarrow^I \pi^* \rightarrow^E v^{*}\]Policy Evaluation
Value Function은 기본적으로 어떤 Policy \(\pi\)에 대해 정의된다. 따라서 다음과 같이 두 가지 특성을 가진다.
- Value Function은 Bellman Equation을 통해 더욱 정확하게 업데이트 할 수 있다.
- Value Function을 정확하게 구했다고 해서 Optimal Value Function이 되는 것은 아니다. 단지 현재 Policy의 정확한 Value Function을 알아냈을 뿐이다.
Policy Evaluation은 아래와 같이 Bellman Equation을 모든 State에 대해 적용하여 Value Function을 보다 정확하게 만드는 과정이다.
\[\eqalign{ v_{k+1}^\pi(s) &= E_\pi [r_{t+1} + \gamma v(s_{t+1}) \lvert s_t = s]\\ &= \Sigma_a \pi (a \lvert s) \Sigma_{s', r} p(s', r \lvert s, a) [r + \gamma v^\pi_k(s')] }\]이와 관련하여 Policy Evaluation은 다음과 같은 특성을 갖는다.
1) Convergence
위의 업데이트 식에 따르면 모든 \(s \in S\)에 대해 \(v_k = v_\pi\)는 Fixed Point가 되고, 따라서 \(k \rightarrow \infty\)라면 \(v_k\)가 \(v_\pi\)에 수렴하는 것이 보장된다. 즉, 모든 State에 대해 위의 식에 따라 반복적으로 Value를 업데이트하게 되면 임의의 \(v_0\)에서 출발했다 할지라도 \(v_\pi\)에 매우 가까워 질 수 있다는 것이다.
2) Full Backup
위의 업데이트 식을 보면 이전 step의 Value Function \(v_k\)를 사용하여 \(v_{k+1}\)을 구한다는 것을 알 수 있다. 그리고 업데이트를 하기 위해서는 현재 state에서 어떤 action을 통해 갈 수 있는 모든 next state의 Value를 알고 있어야 한다. DP의 이러한 특성을 Full Backup이라고 표현한다.
3) Algorithm

위와 같이 반복적으로 업데이트하여 \(v_\pi\)와 매우 근접한 Value Function을 구할 수 있다. 모든 State 각각에 대해 업데이트를 수행하게 되며(Full Backup) 전체 반복문의 탈출 조건은 업데이트의 크기 \(\Delta\)가 일정 수준 이하인 경우로 설정(Fixed Point Algorithm)하고 있다. 참고로 모든 State에 대해 차례대로 업데이트 하는 것을 Sweep이라고 한다.
Policy Improvement
위에서 언급한대로 Value Function을 정확하게 아는 것만으로는 Optimal Value Function를 구할 수 없다. 하지만 Value Function을 알고 있다면 보다 나은 Policy가 무엇인지 힌트를 얻을 수 있다.
\(q\) and \(v\)
이와 관련하여 Policy와 Value Function이 가지는 의미를 다시 한 번 짚고 넘어가고자 한다.
- Policy \(\pi(a \lvert s)\): 어떤 State \(s\)에서 어떤 Action \(a\)을 선택할 것인지 알려주는 함수
- \(v(s)\): 어떤 State \(s\)에 있을 때 기대되는 Return
- \(q(s, a)\): 어떤 State \(s\)에서 어떤 Action \(a\)을 수행했을 때 기대되는 Return
Policy Evaluation을 통해 충분히 정확한 \(v_\pi\)를 구했다면 다음과 같이 충분히 정확한 \(q_\pi\)또한 구할 수 있다.
\[q_\pi(s,a) = \Sigma_{s', r} p(s', r \lvert s, a) [ r + \gamma v_\pi(s') ]\]더 좋은 Policy, 즉 어떤 State에서 현재보다 기대 Return을 높일 수 있는 Action을 선택하는 것은 \(q\)와 \(v\) 간의 크기를 비교하는 것과 관련이 깊다. 왜냐하면 어떤 State \(s\)와 Action \(a\)에 있어 \(q(s,a) \geqq v(s)\)가 성립한다는 것은 \(s\)에서 단순히 현재 Policy \(\pi\)를 따르는 것보다 일단 한 번 Action \(a\)를 선택하고, Next State에서부터 \(s'\)를 따르는 것이 더 낫다는 것을 의미하기 때문이다.
\[q_\pi(s, \pi'(s)) \geqq v_\pi(s)\]그리고 모든 State \(s \in S\)에 대해 위와 같은 공식이 성립한다면 \(\pi'\)는 \(\pi\)보다 더 좋은 Policy라고 할 수 있다.
Greedy Policy
그렇다면 \(v, q\)를 알고 있는 상황에서 Policy를 최적으로 업데이트하는 방법은 무엇일까. 아마도 매 State \(s\)가 주어져 있을 때 \(q(s, a)\)가 가장 큰 Action \(a\)를 선택하는 방법일 것이다. 즉 매 State에서 Greedy한 선택을 하는 것이다.
\[\eqalign{ \pi'(s) &= \arg_a \max q_\pi (s,a)\\ &= \arg_a \max \Sigma_{s', r} p(s',r \lvert s, a)[r + \gamma v_\pi (s')] }\]이와 같이 Value Function에 기반하여 더 나은 Policy를 구하는 방법을 Policy Improvement라고 한다. 그리고 \(\pi = \pi^*\)인 경우를 제외하고는 Policy Improvement를 따를 때 항상 더 좋은 Policy를 만든다.
Policy Iteration Algorithm

정리하자면 Policy Iteration는 위와 같이 표현할 수 있다. Finite MDP에서는 Policy의 개수도 유한하며 이 경우 Policy Iteration의 수렴성이 보장된다고 한다.
Generalized Policy Iteration
Policy Evaluation과 Policy Improvement는 다음과 같은 특성을 가진다고 한다.
- Value Function은 Policy가 일관적일 때(consistent) 안정적이다.
- Policy는 Value Function의 Greedy가 변화하지 않을 때 안정적이다.
이를 그림으로 정리하자면 Policy Iteration은 다음과 같이 표현할 수 있다.
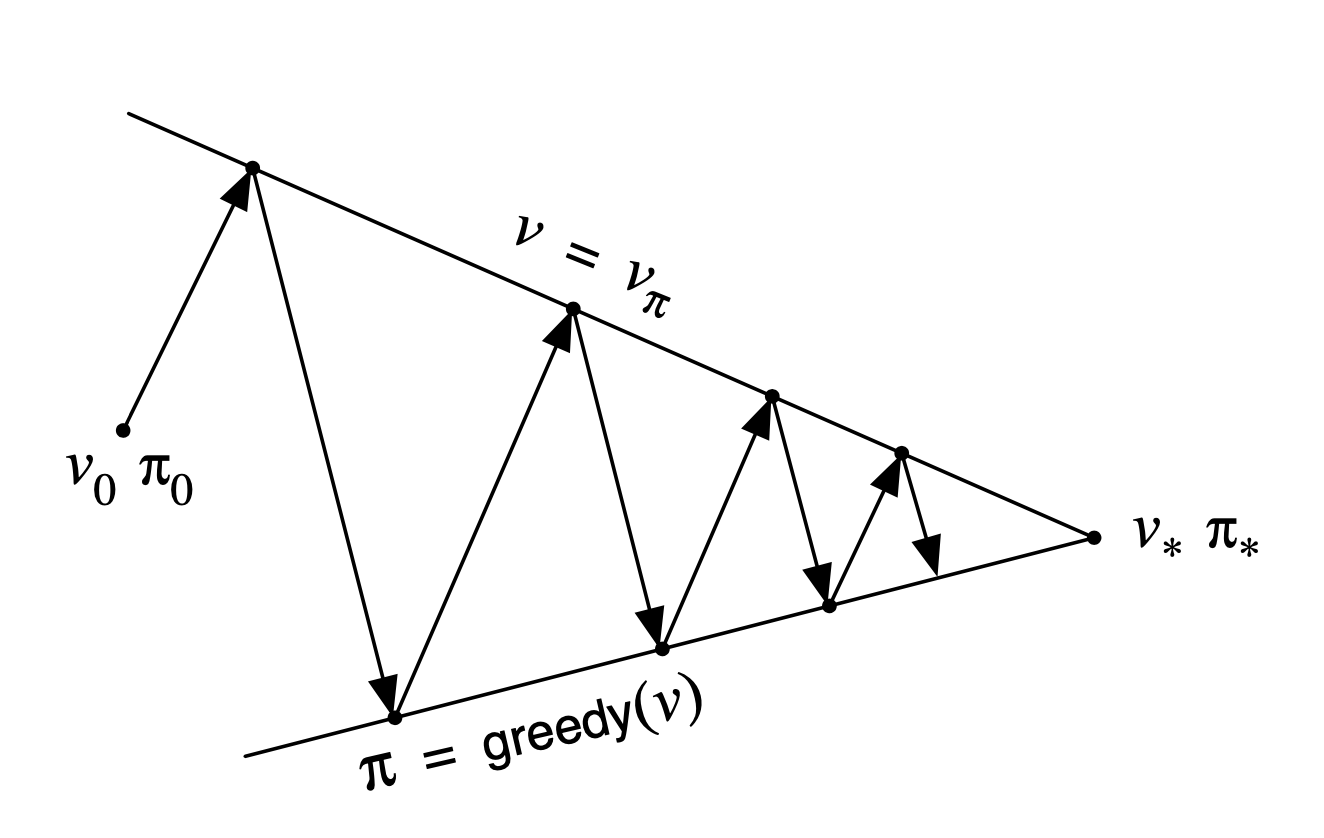
Policy Evaluation과 Policy Improvement를 통해 안정적으로 Value Function과 Policy가 업데이트 된다면 Optimal Value Function, Optimal Policy로 수렴할 수 있다. 뒤집어 이야기하면 Evaluation과 Improvement로 인한 변화가 거의 없다면 Optimal에 충분히 가까워진 것으로 볼 수 있다.
Various DP Method
Policy Iteration은 수렴성이 보장되지만 (1) 모든 State에 대해 Value를 구해야 한다는 점 (2) Value Function이 수렴할 때까지 무한히 반복해야 한다는 점 때문에 연산량이 많고 시간이 오래 걸린다는 단점을 가지고 있다. 이를 해소하기 위해 다음과 같이 보다 효율적인 방법들이 제시되었다.
1) Value Iteration
Value Iteration은 수렴은 하지 않았으나 적절한 수준에서 Policy Evaluation을 멈추고(Truncated) Policy Improvement를 수행하는 방법이다.
- Policy Iteration = Multi Evaluation Sweep + Single Improvement Sweep
- Value Iteration = Single Evaluation Sweep + Single Improvement Sweep
Value Iteration은 Policy가 달라지면 Value Function을 다시 구해야 한다는 점에서 정확한 Value를 구하는 데에 너무 많이 투자할 필요가 없다는 점에서 착안한 방법이다. Discounted Finite MDP 환경에서라면 Value Iteration를 통해 보다 빠른 수렴이 보장된다고 한다.
2) Asynchronous Dynamic Programming
Value Iteration이 Policy Evaluation의 횟수에 관한 것이었다면 Asynchronous Dynamic Programming는 Policy Evaluation의 방식에 관한 것이다. 구체적으로 Policy Evaluation에서 모든 State에 대한 Value를 한 번씩 업데이트하는 것이 아니라 각 State에 대한 업데이트 횟수와 순서를 달리하더라도 수렴이 보장된다는 것을 활용하는 방법이다. 이를 만족하기 위해서는 다음과 같은 두 조건을 만족해야 한다고 한다.
- 업데이트 Sequence {\(s_k\)}의 순서와 중복 여부는 무관하나 모든 \(s \in S\)가 하나 이상은 포함되어야 한다.
- Discount Factor는 \(0 \leqq \gamma < 1\)를 만족해야 한다.
이러한 특성이 전체 연산량을 줄여주는 것은 아니지만 한 번 업데이트 할 때 모든 State를 차례대로 Sweep할 필요가 없기 때문에 필요에 따라 유연한(Flexible) 업데이트가 가능하다. 이러한 특성을 통해 충분히 정확한 Value를 알고 있거나, Optimal을 찾는 데에 딱히 중요하지 않은 State에 대해서는 적게 업데이트하는 등 보다 효율적인 업데이트가 이뤄질 수 있다.
Efficient but Limited
DP를 이용하여 강화학습의 문제를 해결하는 방법은 매우 오래 전에 고안된 것으로, 당시에는 기존 방법과 비교해 볼 때 다음과 같은 장점을 가져 각광받았다.
- Direct Search보다 빠르게 Optimal Policy를 찾을 수 있다.
- Linear Programming보다 넓은 State Space를 커버할 수 있다.
특히 컴퓨터 연산 속도의 발전으로 DP 방법을 통해 수백만 State를 가지는 Finite MDP 환경에서도 최적 Policy를 찾을 수 있다고 한다. 하지만 기본적으로 DP를 강화학습에 적용하는 것은
- Model에 대한 완벽한 정보를 가정한다.
- 매우 큰 연산량을 필요로 한다.
라는 점에서 다소 제한적이며, 현대에 들어서는 직접적으로는 사용되지 않는다. 다만 DP 알고리즘의 많은 내용들은 최근의 강화학습 알고리즘의 근간을 이룬다는 점에서 매우 중요하다.