Optimization Introduction

• Introduction to Optimization, 4th Edition(Chong, Zak-An)의 Chapter 6의 내용을 참고하였습니다.
• Update at: 21.07.29

Optimization Problem

\[\eqalign{ \text{minimize } &f(x)\\ \text{subject to } &x \in \Omega }\]

최적화 문제란 위의 수식과 같이 Constraint set(Feasible set) \(\Omega\) 내에서 어떤 Objective Function \(f: \mathbb{R}^n \rightarrow \mathbb{R}\)의 값을 최소화하는 어떤 점 \(x^*\)를 찾는 문제를 말한다. 여기서 \(\Omega = \mathbb{R}\) 인 경우, 즉 Objective Function의 Domain과 Constraint set이 동일한 경우에는 사실상 제약 조건이 없다고 할 수 있으므로 Unconstrainted Optimization Problem 이라고 한다. 반대로 \(\Omega < \mathbb{R}\) 인 경우에는 Constrainted Optimization Problem이라고 부른다.

Global Minimizer & Local Minimizer

Objective Function \(f\)의 값을 최소화하는 점 \(x^*\)를 찾는 것이 Optimization Problem의 목표라고 했는데, 이때 \(x^*\)를 Global Minimizer라고 부른다. 보다 구체적으로 Global Minimizer는 Constraint Set에 속한 모든 점 \(x\) 중에서 \(f(x)\)의 값이 가장 작은 점을 의미하며, 다음과 같이 표현한다.

\[f(x^*) = \min_{x \in \Omega} f(x) \\ x^* = \arg\min_{x \in \Omega} f(x)\]

Local Minimizer는 전체 Constraint Set이 아니라, 어떤 점이 있을 때 그것의 주변부와만 비교하여 \(f\)의 값이 가장 작은 지점을 말한다. Introduction to Optimization(p.82)에서는 다음과 같이 정의한다.

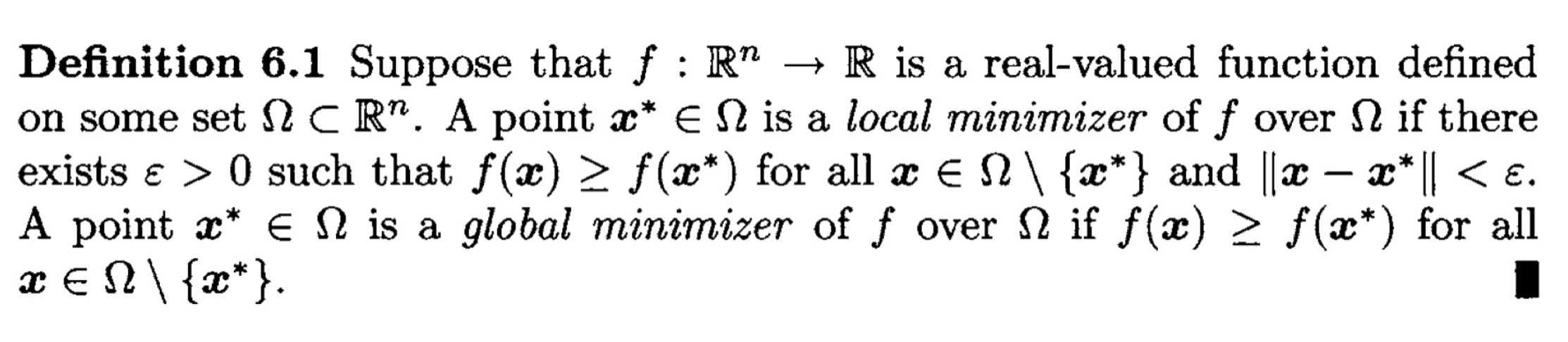
하나씩 풀어보면 다음과 다음과 같이 정리할 수 있다.

• Local이라는 것은 어떤 점 \(x\)가 있다고 할 때 \(\| x' - x \| < \epsilon\)을 만족하는 모든 \(x'\)를 의미한다.
• 모든 \(f(x')\)보다 \(f(x)\)가 더 작거나 같으면 \(x\)는 Local Minimizer 이다.
• \(\epsilon\)은 양수이기만 하면 되며, 아무리 작더라도 항상 \(f(x) \leq f(x')\)를 만족하는 \(\epsilon\) 하나만 찾으면 된다.

Local minimizer and Directional derivatives

Local Minimizer의 특징 중 하나는 가능한 모든 방향으로의 Directional derivative \(\boldsymbol{d}^T \nabla f(x^*)\) 가 항상 0보다 크거나 같다는 것이다(p.85).

여기서 feasible direction \(\boldsymbol{d}\) 이란 아래 그림을 통해 보면 보다 쉽게 이해할 수 있다. 기준점 \(x\)에서 \(\boldsymbol{d_1}\) 방향으로 \(\alpha_1\)의 크기만큼 이동한 점 \(x + \alpha_1 \boldsymbol{d_1}\) 사이의 모든 점들은 feasible set \(\Omega\)에 포함되므로, \(\boldsymbol{d_1}\)은 feasible direction이다. 반면 \(\boldsymbol{d_2}\)의 경우에는 \(\alpha_2\)를 아무리 작게 잡아도 포함될 수 없으므로 feasible direction이 아니다.