Convex Optimization Introduction

• updated at : 20.10.28

Convex Optimization

Optimization이란 주어진 제약 조건 하에서 최적의 경우를 찾는 것이다. Optimization은 문제는 제약 조건과 목적 함수를 정의하는 것과 정의된 목적 함수와 제약 조건에 따라 최적의 해를 찾는 두 단계로 나누어 볼 수 있고, 각각을 Problem Design과 Problem Solving 이라고 한다. Optimization 문제를 푼다고 하면 Problem Solving을 먼저 떠올리는 경향이 있지만 추상적인 문제를 정확하게 수식으로 표현하는 Problem Design 과정 또한 매우 중요하다.

Convex Optimization Problem Design

Optimization Problem Design은 수학적으로 말해 아래와 같은 형태를 갖는 적절한 Optimization Formulation을 도출하는 것을 말한다.

\[\eqalign{ & \min_x \ f(x)\\ & \ s.t. \eqalign{ & g(x) \leq 0 \\ & h(x) = 0 } }\]

그리고 Convex Optimization이란 Optimization Formulation의 특별한 형태로서, 다음과 같은 조건을 만족하는 경우를 말한다.

• Objective Function: \(f(x)\)가 Convex Function이다.
• Inequality Constraint \(g(x)\)가 Convex Function이다.
• Equality Constraint: \(h(x)\)가 Affine Function이다.
• Domain: \(x \in C\)일때 \(C\)는 Convex Set이다.

Feasible set of convex optimization problem is convex

Convex Optimization 문제의 가장 중요한 성질 중 하나는 Convex Optimization Problem 의 Feasible set 은 Convex set이라는 것이다.

• Equality Constraint -> Convex(Affine)
• Inequality Constraint -> Convex
• Intersection of Convex -> Convex

Convexity

Convex Optimization이 무엇인지 정확히 알기 위해서는 Convex Set과 Convex Function이 무엇인지 알아야 한다.

Convex Set

어떤 집합 \(C\)가 Convex하다는 것은 다음과 같이 정의된다.

\[\begin{multline} \shoveleft \textbf{Definition: } \text{ The set } C \text{ is convex when } \\ \theta x + ( 1 - \theta) y \in C \qquad \forall x, y \in C \qquad \\ \shoveleft \text{ where } 0 \leq \theta \leq 1 \end{multline}\\\]

수식의 의미를 보다 쉽게 이해하기 위해 아래 이미지를 보자. 왼쪽 이미지의 경우 집합의 어떤 a, b를 선택하더라도 두 원소를 잇는 선분 또한 집합에 포함된다. 반면 오른쪽 이미지에서는 두 원소 a’, b’를 통해 확인할 수 있듯 위 식을 항상 만족하지는 못한다. 이와 같이 집합의 어떤 두 원소를 잇는 선분이 항상 그 집합에 포함되는 집합을 Convex Set이라고 한다.

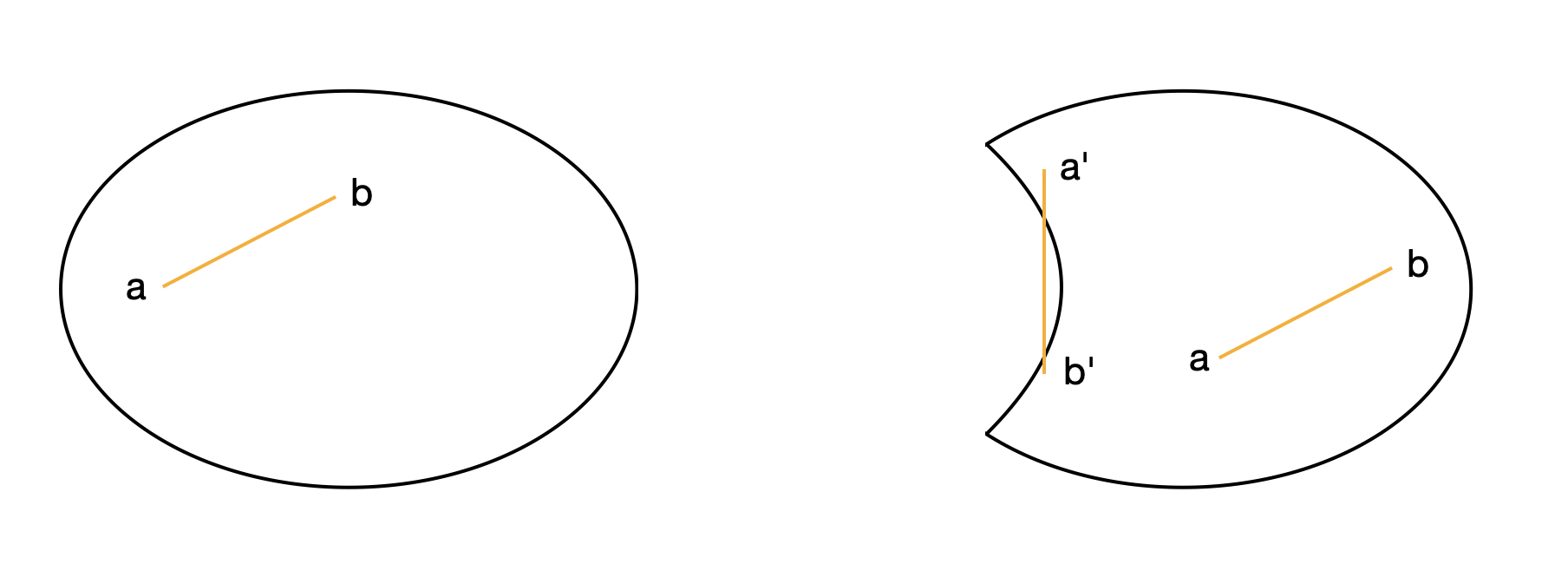
참고로 Convex Hull이란 어떤 Non-Convex Set에 대해 그것을 모두 포함하는 가장 작은 Convex Set을 말한다. 위의 오른쪽 Non-Convex Set에 대한 Convex Hull은 다음 파란 점선과 같이 구해진다.

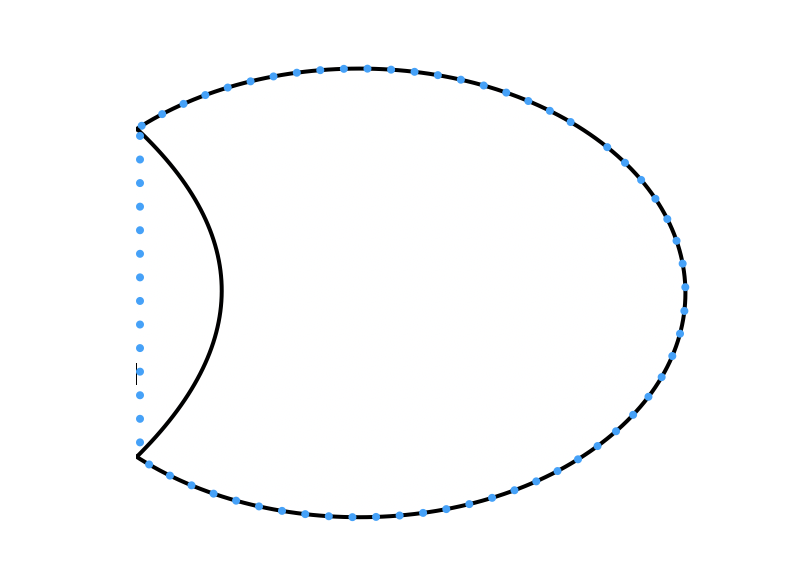
Convex Function

Convex Function는 수학적으로 다음과 같이 정의할 수 있다.

\[\begin{multline} \shoveleft\textbf{Definition: } \text{The function } f \text{ is convex function } \text{when } f \text{ satisfy } \\ f(\theta x + (1 - \theta) y) \leq \theta f(x) + (1 - \theta)f(y) \\ \shoveleft \text{ where } 0 \leq \theta \leq 1, \forall x, y \in Dom f \\ \end{multline}\]

Convex Function 의 Epigraph 는 항상 Convex Set 이다.

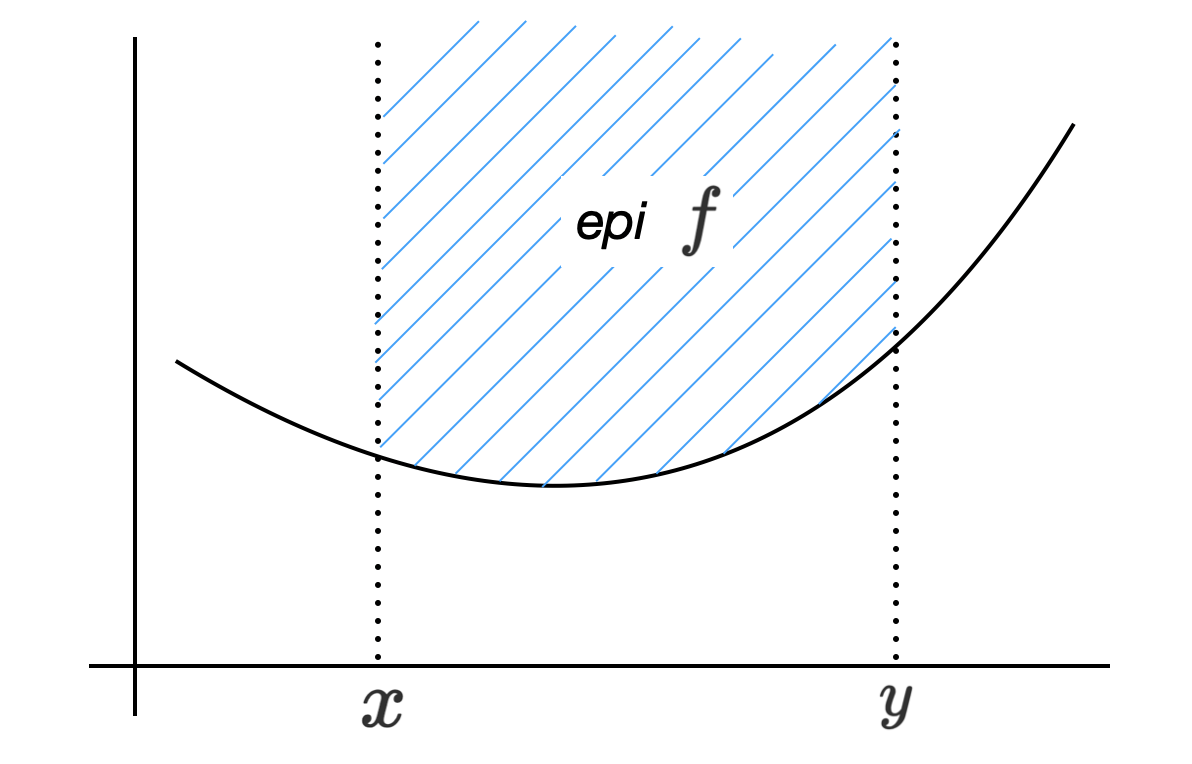
또한 부등호를 등호로 바꾸면 Strict Convex 라고 한다.

\[\begin{multline} \shoveleft\textbf{Definition: } \text{The function } f \text{ is strict convex function } \text{when } f \text{ satisfy } \\ f(\theta x + (1 - \theta) y) < \theta f(x) + (1 - \theta)f(y) \\ \shoveleft \text{ where } 0 \leq \theta \leq 1, \forall x, y \in Dom f \\ \end{multline}\]

\(y = ax\) is Convex Function

1차 함수 \(y = x\) 또한 위의 정의를 만족하므로 Convex Function 이다. 이러한 점에서 보면 Convex Optimization에서 말하는 Convex가 우리가 상상하는 ‘볼록’하다는 것에는 차이가 있으며, Convex Optimization에서 Convex의 의미를 볼록이라는 표현에 집중하기 보다는 Convex Set을 정의하는 수식으로 받아들이는 것이 적절하다.

Local and Global Optima

Convex Function의 가장 큰 특징 중 하나는 Local optima 가 곧 Global optima 라는 것이다. 즉 Local optima 를 찾으면 그것이 곧 Global optima 가 된다.

Local optima 는 어떤 점 \(x\)가 있다고 할 때, 이 점의 주변에 있는 모든 점 \(z\)들에 대해 \(f(x) <= f(z)\) 가 성립하는 \(x\)를 말한다. 수학적으로는 다음과 같이 표기할 수 있다.

\[f(z) >= f(x) \qquad \text{ where } z \text{ is feasible and } \| z -x \|_2 \leq R\]

이는 귀류법으로 접근하면 쉽게 증명할 수 있다. \(x\) 외에 또다른 Local optima \(y\) 가 있다고 가정해보자. 그리고 함수 \(f\) 는 Convex Function 이므로 다음이 성립해야 한다.

\[f(\theta x_1 + (1 - \theta) x_2) \leq \theta f(x_1) + (1 - \theta)f(x_2)\]

두 개의 local optima \(x, y\)가 모두 Convex Set 의 원소이므로 다음과 같은 \(z\) 또한 feasible 하다.

\[z = \theta x + (1 - \theta) y\]

이때 세 가지 경우의 수를 나누어 생각해 볼 수 있다.

1. \(f(x) < f(y)\) 인 경우

\(y\)는 Local optima 이므로 다음이 성립한다.

\[f(y) \leq f(z)\]

또한 \(x, y\) 모두 Convex Set의 원소이므로 다음이 성립한다.

\[f(\theta y + (1 - \theta) x) \leq \theta f(y) + (1 - \theta) f(x)\]

좌변은 \(f(z)\)로 치환할 수 있고, 우변은 \(f(x) < f(y)\) 이므로 \(f(y)\) 보다 작다.

\[f(z) \leq \theta f(y) + (1 - \theta) f(x) < f(y)\]

이렇게 되면 \(f(y) \leq f(z)\) 와 모순된다. 따라서 성립할 수 없다.

2. \(f(y) \leq f(x)\) 인 경우

위에서 \(x, y\)만 스왑하여 동일하게 증명할 수 있다.

3. \(f(x) = f(y)\) 인 경우

첫 번째와 비슷하게 전개하되, 우변이 \(f(x) = f(y)\) 이므로 등호가 된다는 점에서 다르다.

\[f(z) \leq \theta f(y) + (1 - \theta) f(x) = f(x) = f(y)\]

이 또한

\[f(z) < f(x) = f(y)\]

이면 Local Optima 의 가정을 만족시키지 못하므로 성립할 수 없다. 하지만

\[f(z) = f(x) = f(y)\]

등호인 경우에는 수식이 성립하는데, Local optima \(x, y\) 의 \(f\) 값이 같으므로 Global optima 가 복수인 상황이 된다(정확하게는 \(x\)와 \(y\) 사이의 모든 값 \(z\)의 \(f(z)\)도 동일해야 한다). Strict Convex Function 에서는 이 또한 만족하지 않기 때문에 유일한 Local Optima 이자 Global Optima 가 된다.