Differentiation of Multivariate Function

• 김홍종 교수님의 미적분학 1,2를 참고하여 개인 공부를 목적으로 작성했습니다.
• Update at: 2021.01.03

Multivariate

다변수 함수(Multivariate Function)란 말 그대로 함수의 입력 변수가 여러 개인 경우를 말한다.

\[f: U \subset \mathcal R^n \rightarrow \mathcal R\]

공역이 \(m\) 차원의 공간, 즉 함수의 출력이 벡터로 주어질 수도 있다.

\[f: U \subset \mathcal R^n \rightarrow \mathcal R^m\]

첫 번째 예시와 같이 출력이 스칼라 값으로 주어지면 실수 함수(Real-Valued Function)라고 하고, 벡터 값으로 주어지면 벡터 함수(Vector-Valued Function)이라고 한다.

Continuous Function

어떤 함수가 주어져 있을 때 미분 가능하려면 그 함수는 연속 함수여야 한다. 조금 더 정확하게 말해 모든 미분 가능한 함수는 연속 함수이다. 미적분학에서 말하는 함수의 연속성(Continuity)이란 다음과 같이 정의된다.

\[\eqalign{ &\text{Let } f: U \subset \mathcal R^n \rightarrow \mathcal R^m \text{ and } p \in U\\ & \text{If and only if } \lim_{x \rightarrow p} f(x) = f(p), \\ &\text{then the function } f \text{ is continuous on } p }\]

한 마디로 함수 \(f\)의 정의역 \(U\)의 한 점 \(p\)가 있다고 할 때 \(f(p)\)와 \(\lim_{x \rightarrow p} f(x)\)가 같으면 \(p\)에서 \(f\)는 연속이라고 할 수 있다. 그리고 함수 \(f\)가 연속이라고 하기 위해서는 정의역 \(U\)의 모든 \(x\)에 대해 연속이어야 한다.

Properties of Continuous Function

연속 함수는 기본적으로 다음과 같은 특성을 가진다.

• 상수 함수는 연속 함수이다.
• 두 연속 함수의 곱과 합 또한 연속 함수이다.
• 두 연속 함수의 합성 또한 연속 함수이다.

Extreme Value Theorem

최대 최소 정리(Extreme Value Theorem)란 유계(Bounded)인 닫힌 집합(Closed Set)에서 정의된 연속 함수는 최대 값과 최소 값을 가진다는 것에 대한 정리로, 해의 존재성을 보장한다는 점에서 연속 함수의 중요한 특성 중 하나라고 할 수 있다. 정리의 결과는 최대 최소의 해가 존재한다는 것으로 명확하지만 조건으로 제시된 내용 중 유계(Bounded)와 닫힌 집합(Closed Set)이라는 특성에 대해서는 정리할 필요가 있다.

우선 닫힌 집합이 무엇인지 정확하게 알기 위해서는 이를 정의하기 위해 사용되는 Open Ball(or Interval, Disk)에 대한 개념부터 알아야 한다.

Open Set & Closed Set

열린 공(Open Ball)이란 아래 식과 같이 어떤 점 P를 중심으로 하고 반지름이 r인 원을 의미한다. 만약 아래 식에서 정의역이 1차원 공간이라면 Open Interval이 되고, 2차원 공간이라면 Open Disk라고 부를 수 있지만 표현 상의 차이이지 의미는 동일하다.

\[\mathcal B^n (p, r) = \{ x \in \mathcal R^n \lvert \ \lvert x - p \rvert < r \}\]

이를 기준으로 부분 집합 \(U\)와의 관계에 따라 \(\mathcal R^n\) 상에 존재하는 모든 점들을 다음 세 가지로 나누어 볼 수 있다.

• 내점: 해당 점을 중심으로 하는 임의의 열린 공이 모두 \(U\)에 포함되는 경우
• 외점: 해당 점을 중심으로 하는 임의의 열린 공이 모두 \(U\)에 포함되지 않는 경우
• 경계점: 해당 점을 중심으로 하는 임의의 열린 공의 일부는 \(U\)에 포함되지만 일부는 그렇지 않은 경우

부분 집합 \(U\)에 포함되는 모든 점이 내점이라면 \(U\)는 열린 집합(Open Set)이라고 한다. 즉 Open Set에는 \(U\)의 경계점은 하나도 포함되어 있지 않다. 반대로 내점과 함께 \(U\)의 모든 경계점이 \(U\)에 포함되는 경우를 닫힌 집합(Closed Set) 이라고 한다.

Bounded Set

유계 집합(Bounded Set)은 지름이 유한한 집합을 말한다. 이때 말하는 지름이란 다음과 같이 집합의 임의의 두 점 사이의 거리의 상한을 의미한다.

\[\text{diam} U = \sup \{ \lvert p - q \rvert \lvert p, q \in U \}\]

Partial Derivative & Directional Derivative

다변수 함수 미분의 특징 중 하나는 변화의 방향이 하나만 존재하는 일변수 함수와 달리 다변수 함수는 변화의 방향이 다양하다는 것이다. 따라서 변화의 방향에 따라 동일한 지점에서도 다양한 미분 값이 계산될 수 있다. 예를 들어 \(n\) 차원 공간이라고 한다면 \(n\)개의 축이 있다는 것을 의미하는데, 각 축의 방향으로 다변수 함수의 순간 변화율을 편미분(Partial Differentiation)라고 하고, 이를 구하는 함수를 편도함수(Partial Derivative)라고 한다. 특정 축이 아닌 임의의 방향에 대해서도 순간 변화율을 구할 수 있는데, 이를 구하는 함수는 방향도함수(Directional Derivative)라고 한다.

Derictional Derivative

벡터 함수 \(f: U \rightarrow \mathcal R\)가 주어져 있을 때, 어떤 점 \(p \in U\)에서 특정한 방향(Vector \(v\))으로의 순간 변화율은 다음과 같이 정의된다.

\[D_v f(p) = \lim_{t \rightarrow 0} { f(p + tv) - f(p) \over t} = \lim_{t \rightarrow 0} { f(p_1 + tv_1, p_2 + tv_2, ..., p_n + tv_n) - f(p_1, p_2, ..., p_n) \over t}\]

이는 다음과 같이 표기하기도 한다. 참고로 우항의 Vertical Line은 Evaluation Bar라고 하며, ‘Evaluated at’의 의미를 가진다.

\[D_v f(p) = {d \over dt}f(p + tv) \biggr\vert_{t=0}\]

\(t\)가 \(0\)으로 무한히 가까워질 때 \(f(p + tv)\)가 변화하는 크기의 비율이라는 의미이다.

Partial Derivative

위의 방향미분은 임의의 방향 \(v\)로의 순간 변화율을 의미하는데, 편미분은 특정한 방향, 즉 공간을 구성하는 축의 방향으로의 순간 변화율이라는 점에서 방향미분의 특수한 예라고도 할 수 있다. 쉽게 말해 편미분은 표준 단위 벡터 방향으로의 방향미분이다.

\[D_{e_k} f(p) = \lim_{t \rightarrow 0} { f(p + te_k) - f(p) \over t} = \lim_{t \rightarrow 0} { f(p_1, p_2, ..., p_k + t ..., p_n) - f(p_1, p_2, ..., p_n) \over t}\]

편미분도 동일하게 다음과 같이 표기할 수 있다.

\[D_{e_k} f(p) = {d \over dt}f(p + te_k) \biggr\vert_{t=0}\]

편미분은 그 특징 상 \(f\)의 입력 값 중 \(k\)번째 입력 값 \(x_k\) 단 하나만 바꾼다. 즉 함수 \(f\)의 입력 값 중 \(x_k\)를 제외한 다른 모든 입력 값들은 상수로 보아도 된다는 것이다. 따라서 다음과 같이 표기하기도 한다.

\[D_{e_k} f(p) = {\partial f \over \partial x_k } (p_1, p_2, ..., p_n) = {\partial f \over \partial x_k } \biggr\rvert_{(p_1, p_2, ..., p_n)}\]

여기서 \(D_{e_k} f = {\partial f \over \partial x_k}\)를 어떤 위치에서 \(e_k\) 방향으로의 편미분 값을 구하는 함수, 즉 편도함수라고 한다.

Gradient

Gradient Vector란 다음과 같이 각 축에 대한 편미분 값으로 이뤄진 벡터이다. nabla \(\nabla\)로 표기하는 것이 일반적이다.

\[\nabla f(p) = ({\partial f \over \partial x_1}(p), {\partial f \over \partial x_2}(p), ..., {\partial f \over \partial x_n}(p))\]

일변수 함수에서는 \(f'(p)\)가 \(p\)에서 접선(Tangetn Line)의 기울기였다면 다변수 함수에서는 \(\nabla f (p)\)가 접평면(Tangent Plane)의 기울기가 된다.

Differentiable Function

다변수 함수 \(f\)가 어떤 한 지점 \(\boldsymbol{p}\)에서 미분 가능하려면 다음과 같은 조건들을 만족해야 한다.

• \(\boldsymbol{p}\)에서 \(f\)에 대한 편미분 값들이 모두 존재한다.
• \(\lim_{\boldsymbol{x} \rightarrow \boldsymbol{p}} { f(\boldsymbol{x}) - f(\boldsymbol{p}) - \nabla f (\boldsymbol{p}) (\boldsymbol{x} - \boldsymbol{p}) \over \vert \boldsymbol{x} - \boldsymbol{p} \vert} = \boldsymbol{0}\) 를 만족한다.

두 번째 조건을 보게 되면 다변수 함수에서 미분 가능한 지점 \(\boldsymbol{p}\)에 접하는 접평면은 기울기가 \(\nabla f (\boldsymbol{p})\)로 유일하게 결정된다는 것을 알 수 있다. 다르게 말하면 다변수 함수 \(f\)를 미분 가능한 지점 \(\boldsymbol{p}\)에서 선형 근사한 결과는 기울기가 \(\nabla f (\boldsymbol{p})\)인 평면이 된다. 이들 조건들은 접평면의 특성과 연관된다.

Tangent line

일변수 함수 \(f\)가 어떤 점 \(p\)에서 미분이 가능하다고 할 때 접선(Tangent Line)은 다음과 같이 나타낼 수 있다.

\[l : f'(p)(x-p) + f(p)\]

그래프로 표현하면 다음과 같다.

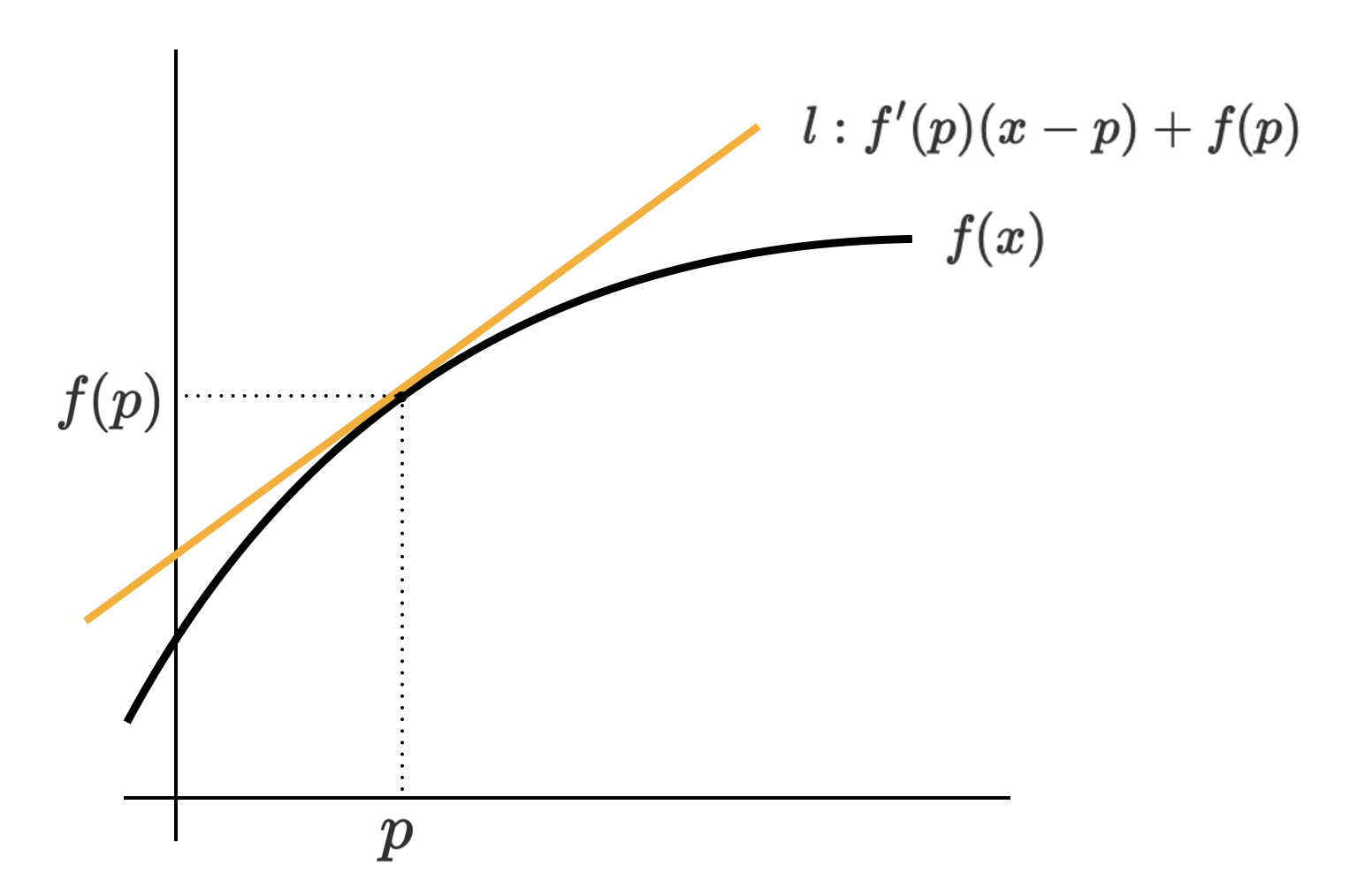
접선의 의미를 미분 계수로도 확인할 수 있다.

\[\eqalign{ &f'(x) = \lim_{t \rightarrow 0} { f(p + t) - f(p) \over t} = \lim_{x \rightarrow p} { f(x) - f(p) \over x - p}\\ \Rightarrow & \lim_{x \rightarrow p} { f(x) - f(p) \over x - p} - f'(x) = 0 \\ \Rightarrow & \lim_{x \rightarrow p} { f(x) - f(p) - f'(p) (x - p) \over x - p} = 0 \\ }\]

여기서 극한 값 내의 \(- f(p) - f'(p) (x - p)\)는 위에서 확인한 접선의 식에 음수를 취한 것과 같다. 이러한 점에서 위 식의 의미를 보면 \(f(x)\)가 접선 \(l: f(p) + f'(p) (x - p)\)에 가까워지는 속도가 \(x\)가 \(p\)에 가까워지는 속도보다 빠르다는 것을 알 수 있다.

Tangent plane

다변수 함수에서는 접선이 아니라 접평면(Tangent Plane)으로 나타난다. 예를 들어 두 개의 입력 값을 받는 함수 \(z = f(x_1, x_2)\)가 있다고 하자. \(z = f(x_1, x_2)\)의 그래프는 한 차원 높은 3차원 공간\((x_1, x_2, y)\)에 존재하므로, 접평면 또한 3차원 공간 상의 한 평면이라고 할 수 있다. \((y, f(\boldsymbol{p}))\)를 지나는 접평면은 다음과 같이 정의된다.

\[y = f(\boldsymbol{p}) + \boldsymbol{a} \cdot (\boldsymbol{x} - \boldsymbol{p})\]

접선의 방정식에서 확인한 수식을 그대로 적용하여 평면이 \(\boldsymbol{p}\)에서 \(f\)를 선형 근사하도록 하면 다음과 같이 접평면 식을 구할 수 있다. 이때 \(\boldsymbol{a}\)는 평면의 기울기 벡터이다.

\[\lim_{\boldsymbol{x} \rightarrow \boldsymbol{p}} { f(\boldsymbol{x}) - f(\boldsymbol{p}) - \boldsymbol{a} (\boldsymbol{x} - \boldsymbol{p}) \over \vert \boldsymbol{x} - \boldsymbol{p} \vert} = \boldsymbol{0}\]

이를 각 컴포넌트 \(x_k\)에 대한 식으로 분리하면

\[\eqalign{ &\lim_{x_k \rightarrow p_k} {f(x_k) - f(p_k) - a_k (x_k - p_k) \over x_k - p_k} = 0\\ &\Rightarrow a_k = \lim_{x_k \rightarrow p_k} {f(x_k) - f(p_k) \over x_k - p_k} \\ &\Rightarrow a_k = {\partial f \over \partial x_k}(p_k) \\ }\]

기울기 벡터 \(\boldsymbol{a} = (a_1, a_2, ..., a_n)\)가 각 축에 있어 \(f\)에 대한 편미분 값이라는 것을 알 수 있다. 다시 말해 다변수 함수에서 접평면의 기울기는 그래디언트 벡터가 된다.

Tangent Plane & Directional Derivative

접평면의 기울기를 구하는 과정에서 사용된 식

\[\lim_{\boldsymbol{x} \rightarrow \boldsymbol{p}} { f(\boldsymbol{x}) - f(\boldsymbol{p}) - \boldsymbol{a} (\boldsymbol{x} - \boldsymbol{p}) \over \vert \boldsymbol{x} - \boldsymbol{p} \vert} = \boldsymbol{0}\]

은 \(\boldsymbol{x} = \boldsymbol{p} + \boldsymbol{v}\)로 하여 다음과 같이 쓸 수도 있다.

\[\eqalign{ &\lim_{\boldsymbol{v} \rightarrow 0} { f(\boldsymbol{p} + \boldsymbol{v}) - f(\boldsymbol{p}) - \boldsymbol{a} ((\boldsymbol{p} + \boldsymbol{v}) - \boldsymbol{p}) \over \vert (\boldsymbol{p} + \boldsymbol{v}) - \boldsymbol{p} \vert} = \boldsymbol{0}\\ \Rightarrow & \lim_{\boldsymbol{v} \rightarrow 0} { f(\boldsymbol{p} + \boldsymbol{v}) - f(\boldsymbol{p}) - \boldsymbol {a} \boldsymbol{v} \over \vert \boldsymbol{v} \vert} = \boldsymbol{0}\\ }\]

\(\boldsymbol{v}\)의 방향과 크기를 분리하여 \(\boldsymbol{v}\)를 동일한 방향을 가지는 단위 벡터 \(\boldsymbol{v'}\)와 크기 \(t\)의 곱으로 나타낸다고 하면 다음과 같다.

\[\eqalign{ & \lim_{t \rightarrow 0} { f(\boldsymbol{p} + t\boldsymbol{v'}) - f(\boldsymbol{p}) - \boldsymbol {a} t\boldsymbol{v'} \over t} = \boldsymbol{0}\\ \Rightarrow & \lim_{t \rightarrow 0} { f(\boldsymbol{p} + t\boldsymbol{v'}) - f(\boldsymbol{p}) \over t} - \boldsymbol {a} \boldsymbol{v'} = \boldsymbol{0}\\ \Rightarrow & \lim_{t \rightarrow 0} { f(\boldsymbol{p} + t\boldsymbol{v'}) - f(\boldsymbol{p}) \over t} = \boldsymbol {a} \boldsymbol{v'}\\ }\]

위 식은 \(\boldsymbol{v'}\) 방향으로의 방향 미분 값과 동일하다.

\[D_{v'} f(\boldsymbol{p}) = \lim_{t \rightarrow 0} { f(\boldsymbol{p} + t\boldsymbol{v'}) - f(\boldsymbol{p}) \over t} = \boldsymbol {a} \boldsymbol{v'}\]

여기서 \(\boldsymbol{a}\)는 \(f\)의 그래디언트 벡터이므로, 어떤 지점 \(\boldsymbol{p}\)에서 특정 방향 \(\boldsymbol{u}\)로의 방향 미분 값은 \(\nabla f(\boldsymbol{p}) \boldsymbol{u}\)임을 알 수 있다.

\[D_{v'} f(\boldsymbol{p}) = \nabla f(\boldsymbol{p}) \boldsymbol{v'}\]