Talyor Series
- 김홍종 교수님의 미적분학 1,2를 참고하여 개인 공부를 목적으로 작성했습니다.
- Update at: 2020.01.02
- References
Approximate Function with Polynomial
테일러 급수(Talyor Series)는 임의의 함수를 다루기 쉬운 다항 함수(Polynomial)로 근사하여 표현하는 방법이다. 근사한다는 점에서 어느 정도의 오차를 감안해야 하지만 테일러 급수를 사용하면 다루기 어려운 함수를 비슷한 다항 함수로 대체할 수 있다는 점에서 함수 또는 모델을 단순하게 만들어 준다는 장점을 가지고 있다.
Little-o \(o(x)\) Notation
어떤 함수를 근사한다는 것은 작은 수준의 오차를 허용하면서 원래 함수보다 더욱 다루기 쉬운 함수를 찾겠다는 것을 의미한다. 그렇다면 ‘작은 수준의 오차’를 어떻게 정의할 것인가가 근사의 정확도를 결정한다고 할 수 있다. 근사의 오차를 표현하는 방법 중 하나로 알고리즘의 시간 복잡도를 평가할 때 사용되는 점근적 표기법 중 하나인 Little-o Notation \(o(x)\)를 사용하는 방법이 있다. 참고로 알고리즘에서 사용되는 Little-o Notation의 정의는 다음과 같다.
\[\eqalign{ &\text{if } \exists \ n_0, c > 0, \text{ such that } 0 \leq f(n) < c g(n) \text{ where } n_0 \leq n \\ &\text{then } f(n) \in o(g(n)) }\]CMU에서 제공하는 Lecture Appendix에서는 Big-O와 Little-o를 다음과 같이 정의한다.
- Big-O: is of the same order as
- small-o: is ultimately smaller than
여기서 “Same Order”라는 것은 동일한 속도로 증가한다는 것을 의미한다. 즉 Big-O는 \(f(x)\)와 기준이 되는 \(g(x)\)가 동일한 속도로 증가한다는 것을, small-o는 \(f(x)\)가 훨씬 더 느린 속도로 증가한다는 뜻을 가진다.
이러한 개념을 함수를 근사하는 데에도 기준으로 사용하는 것도 가능한데, 가장 쉬운 예를 들면 원점(\(0\))에서 어떤 함수 \(f(x)\)와 가장 가까운 함수 \(p(x)\)를 찾고자 할 때 두 함수가 가지는 오차의 크기(\(f(x) - p(x)\))가 기준 함수 \(g(x) = x\)보다 빠르게 줄어드는지 확인하여 근사 여부를 판단하겠다는 것이다. 참고로 위의 시간 복잡도를 위해 사용하는 little-o와 차이가 있다면 위에서는 입력의 크기가 무한히 증가하는 경우, 즉 \(x \rightarrow \infty\)를 가정했다면 여기서는 \(x \rightarrow 0\)을 가정하고 있다.
\[f(x) - p(x) = o(x)\]위 식이 성립한다면 \(g(x) = x\)보다 \(p(x)\)가 \(f(x)\)에 더 빠르게 원점에 시작하는 지점이 존재하게 된다.
When \(p(x)\) is First Order
기준을 세웠으니 이제 근사 함수 \(p(x)\)를 구할 차례이다. 테일러 급수는 어떤 함수든 간에 다항 함수로 근사할 수 있다는 뜻이라고 했으므로 \(p(x)\)는 다항함수가 되어야 하는데, 다항 함수 중에서도 가장 기초적인 1차 함수(First Order)으로 가정해보자.
\[p(x) = a + bx\]이때 \(x \rightarrow 0\)일 때 \(f(x) - p(x) = o(x)\)를 만족하기 위해서는 \(f(x)\)와 \(p(x)\)가 원점에서 서로 같은 값을 가져야 하고, 비교 대상이 되는 \(g(x) = x\)보다 원점에 접근하는 속도(근사 함수의 오차가 줄어드는 속도)가 더 빨라야 한다. 이는 수식으로 다음과 같이 표현할 수 있다.
\[\eqalign{ &1. \ {f(0) - p(0) = 0}\\ &2. \ {\lim_{x \rightarrow 0} {f(x) - p(x) \over x} = 0}\\ }\]첫 번째 조건을 통해 \(f(0) = a\)여야 함을 확인할 수 있고,
\[\eqalign{ f(0) - p(0) &= 0\\ f(0) - (b \cdot 0 + a) &= 0\\ f(0) - a &= 0\\ f(0) &= a\\ }\]이어 두 번째 조건에서 \(f'(0) = b\)를 만족해야 함을 알 수 있다.
\[\eqalign{ 0 &= \lim_{x \rightarrow 0} {f(x) - p(x) \over x}\\ &=\lim_{x \rightarrow 0} {f(x) - (a + bx) \over x} \\ &=\lim_{x \rightarrow 0} {f(x) - (f(0) + bx) \over x} \\ &=\lim_{x \rightarrow 0} {f(x) - f(0) \over x - 0} - b \\ &= f'(0) - b \\ }\]따라서 \(f(x)\)를 근사하는 1차 함수 \(p(x)\)를 다음과 같이 정의하면 \(f(x) - p(x) = o(x)\)를 만족한다.
\[p(x) = f'(0)x + f(0)\]Over the First Order
지금까지는 \(f(x) - p(x) = o(x)\)인 경우, 즉 근사 값의 오차가 기준 함수 \(g(x) = x\)보다 빠른 경우에 대해서만 살펴보았다. 그런데 여기서 근사 값이 줄어드는 속도를 보다 빠르게 기준을 높이는 것도 가능한데, 단순하게 말하면 기준 함수의 차수를 높이면 된다.
\[f(x) - p(x) = o(x^n)\]아래 그림을 보면 차수가 높아질수록 기준이 점차 엄격해진다는 것을 직관적으로 확인할 수 있다. 빨간 선부터 검은 선까지 차례대로 각각 \(y=x, x^2, x^3, x^4, x^5\)의 그래프이다.
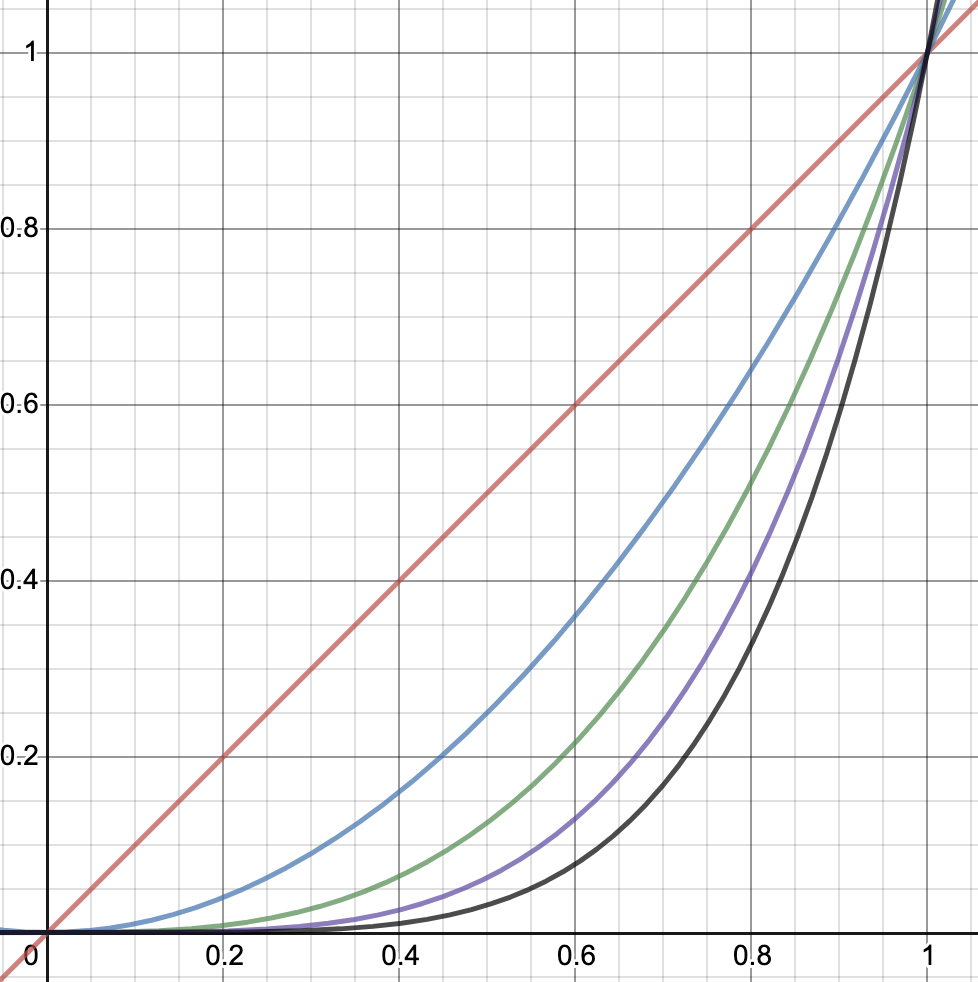
계속해 위의 조건을 만족하기 위해서는 \(f(x) - p(x)\)가 \(n\)차 미분이 가능한 함수여야 한다는 조건 외에도 1차 함수인 경우와 마찬가지로 다음 두 조건을 만족해야 한다.
\[\eqalign{ &1. \ {f(0) - p(0) = 0}\\ &2. \ {\lim_{x \rightarrow 0} {f(x) - p(x) \over x^n} = 0}\\ }\]첫 번째 조건은 \(g(x) = x\)인 경우와 동일하고 두 번째 조건에서 분모의 차수가 \(n\)으로 늘어난 것이 유일한 차이이다. 그런데 이를 만족하기 위해서는 다음과 같이 \(1\)차 미분부터 \(n\)차 미분까지의 값들이 모두 0이 되어야 한다. (Notation을 단순히 하기 위해 \(h(x) = f(x) - p(x)\)로 표기했다)
\[h(0) = h'(0) = h''(0) = ... = h^{(n)}(0) = 0\]이에 대한 증명은 다음과 같이 로피탈의 정리를 적용하는 것에서 시작한다.
\[{\lim_{x \rightarrow 0} {h(x) \over x^n} = \lim_{x \rightarrow 0} {h'(x) \over n x^{(n-1)}} = \lim_{x \rightarrow 0} {h''(x) \over n(n-1) x^{(n-2)}} = ... = \lim_{x \rightarrow 0} {h^{(n-1)}(x) \over n! x}}\]여기서 \(h(0) = h'(0) = h''(0) = ... = h^{(n-1)}(0) = 0\)이라고 한다면 다음과 같이 식을 정리할 수 있다.
\[\lim_{x \rightarrow 0} {h(x) \over x^n} = {h^{(n)}(0) \over n!}\]이에 더해 \(h^{(n)}(0) = 0\) 이라면 최종적으로
\[\lim_{x \rightarrow 0} {h(x) \over x^n} = {h^{(n)}(0) \over n!} = 0\]이 성립하여 \(h(x) = o(x^n)\)이라고 할 수 있다. 다시 말해 \(h(x) = o(x^{(n-1)})\)이고, \(h^{(n)}(0) = 0\)이면 \(h(x) = o(x^{(n)})\)라는 것이다. 이때 \(n=1\)인 경우에 대해서는
\[\eqalign{ &1. \ {f(0) - p(0) = 0}\\ &2. \ h'(0) = 0\\ }\]를 만족하면 성립한다는 것을 확인했으므로 \(n=2\)이면 이에 더해 \(\ h''(0) = 0\)을, \(n=3\)이면 이에 더해 \(\ h^{(3)}(0) = 0\)을 반복적으로 만족해야 한다는 것을 알 수 있다(수학적 귀납법). 따라서 \(n=n\)인 경우에는
\[h(0) = h'(0) = h''(0) = ... = h^{(n)}(0) = 0\]를 만족해야 한다.
Taylor Series
\(f(x) - p(x) = o(x^n)\)을 만족하는 근사 다항식 \(p(x)\)를 테일러 다항식(Taylor Polynomial)이라고 한다. 어떤 함수 \(f(x)\)에 대한 테일러 다항식은 다음과 같이 \(T_n f(x)\)로 표기한다.
\[\eqalign{ T_n f(x) &= p_0 + p_1 x + p_2 + x^2 + ... + p_n x^n\\ &= f(0) + f'(0) x + ... + {f^{(n)}(0) \over n!} x^n }\]앞서 언급한 것처럼 \(n\)의 크기가 크면 클수록 근사의 정확도는 높아진다. \(n \rightarrow \infty\)일 때 위 식을 테일러 급수(Taylor Series)라고 한다.
Not on origin
원점(0)을 기준으로 하지 않는 경우에 대해서도 일반화하여 테일러 급수를 표현할 수 있다. 이를 위해서는 어떤 임의의 한 지점 \(a\)에서 아래 식을 만족해야 한다.
\[\lim_{x \rightarrow a} { f(x) - p(x) \over (x - a)^n} = 0\]이 때의 테일러 다항식은 다음과 같이 구해진다.
\[\eqalign{ T_n^a f(x) &= \Sigma_{k=0}^n {f^{(k)}(a) \over k!}(x - a)^k\\ &= f(a) + f'(a) (x - a) + ... + {f^{(n)}(a) \over n!}(x-a)^n }\]테일러 급수의 정확도는 테일러 다항식의 \(n\) 뿐만 아니라 기준점 \(a\)에 따라서도 결정된다. 정리하자면 \(T_n^a f(x)\)의 차수 \(n\)이 커지면 커질수록, 구하고자 하는 지점이 \(f(b)\)일 때 테일러 다항식의 기준 점 \(a\)와 \(b\)가 가까울수록 근사의 정확도는 높아지게 된다.