Outper Product and Determinant
- 3Blue1Brown의 다음 영상을 참고하여 작성했습니다.
- update at : 2020.10.02
Determinant
외적(Outer Product)이 무엇인지 알아보기 전에 행렬식(Determinant)의 의미를 먼저 확인할 필요가 있다. 행렬식은 역행렬의 존재 여부를 확인할 때 사용하는 식이라고 할 수 있으며 2차원 행렬에서는 다음과 같이 정의된다.
\[\det ( \begin{bmatrix} a && b \\ c && d\\ \end{bmatrix} ) \ = \ {ad - bc}\]3차원 행렬은 다음과 같다.
\[\det ( \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{bmatrix} ) \ = \ a \det ( \begin{bmatrix} e && f \\ h && i\\ \end{bmatrix} ) - b \det ( \begin{bmatrix} d && f \\ g && i\\ \end{bmatrix} ) + c \det ( \begin{bmatrix} d && e \\ g && h\\ \end{bmatrix} )\]Geometric Meaning of Determinant
어떤 행렬의 행렬식은 기하학적으로 행렬을 구성하는 칼럼 백터들로 만들 수 있는 공간의 크기를 의미한다. 예를 들어 2개의 칼럼 벡터를 가지는 \(2 \times 2\) 행렬 \(A, B\)의 행렬식과 각 칼럼으로 만들 수 있는 평면(2차원 이므로)의 크기는 다음과 같이 같음을 알 수 있다.
\[\eqalign{ &\det ( A ) = \det ( \begin{bmatrix} 1 && 0 \\ 0 && 1 \\ \end{bmatrix} ) = 1 \\ &\det ( B ) = \det ( \begin{bmatrix} 3 && {1 \over 2} \\ {1 \over 2} && 2 \\ \end{bmatrix} ) = 5.75 \\ }\]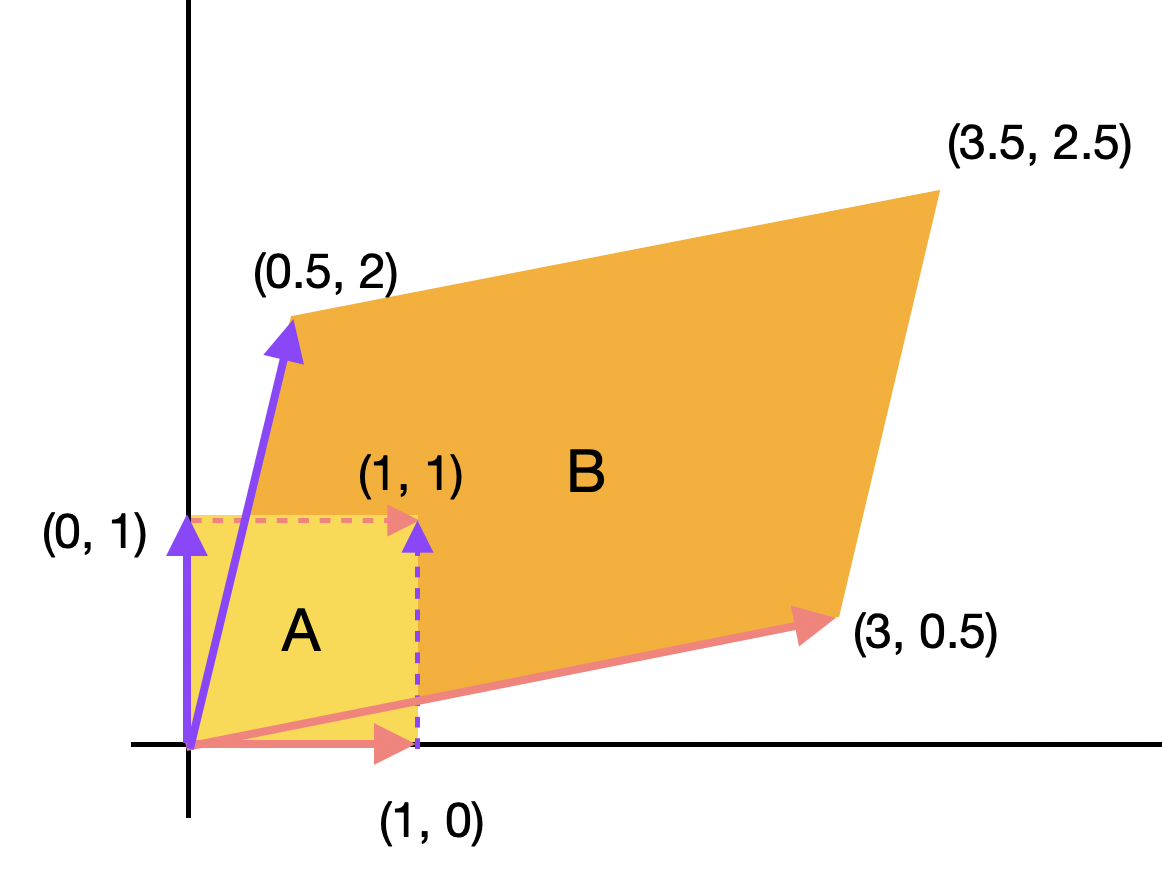
행렬식이 0인 경우, 즉 역행렬이 존재하지 않는 경우는 다음과 같이 각 칼럼 벡터의 Span이 겹치는 경우라고 할 수 있다. 역행렬을 어떤 행렬의 선형 변환의 결과를 되돌릴 수 있는 행렬이라고 생각한다면, 정방향의 선형 변환의 결과 Span이 줄어들기 때문에 역방향으로 되돌릴 때에 해가 무수히 많거나 없게 된다.
\[\det ( C ) = \det ( \begin{bmatrix} 1 && {3 \over 2} \\ 2 && 3 \\ \end{bmatrix} ) = 0 \\\]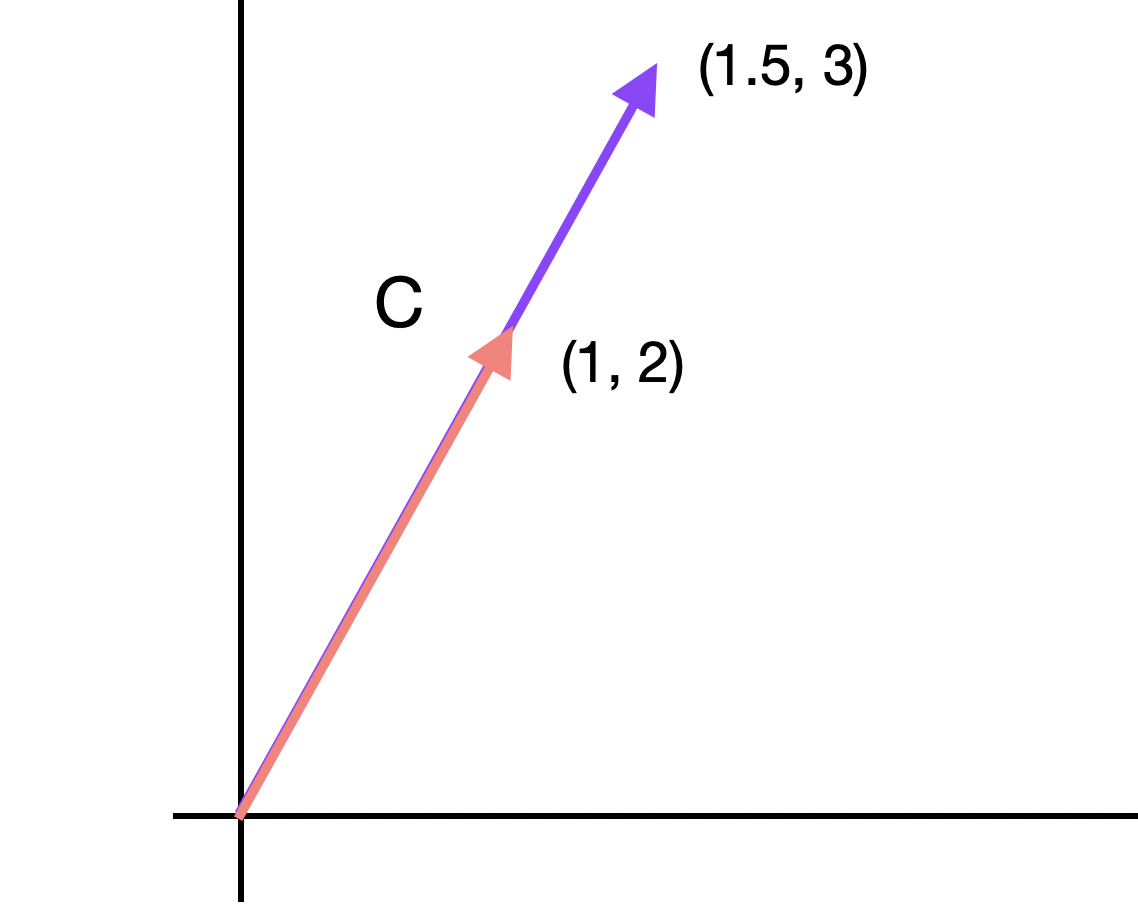
행렬식의 값이 음수가 나올 수도 있는데 이는 면적이 음수라는 것이 아니라 원 평면에서의 단위 벡터가 뒤집어졌다는 것(flip)을 의미한다.
\[\eqalign{ &\det ( A' ) = \det ( \begin{bmatrix} 0 && 1 \\ 1 && 0 \\ \end{bmatrix} ) = -1 \\ &\det ( B' ) = \det ( \begin{bmatrix} {1 \over 2} && 2 \\ 3 && {1 \over 2} \\ \end{bmatrix} ) = -5.75 \\ }\]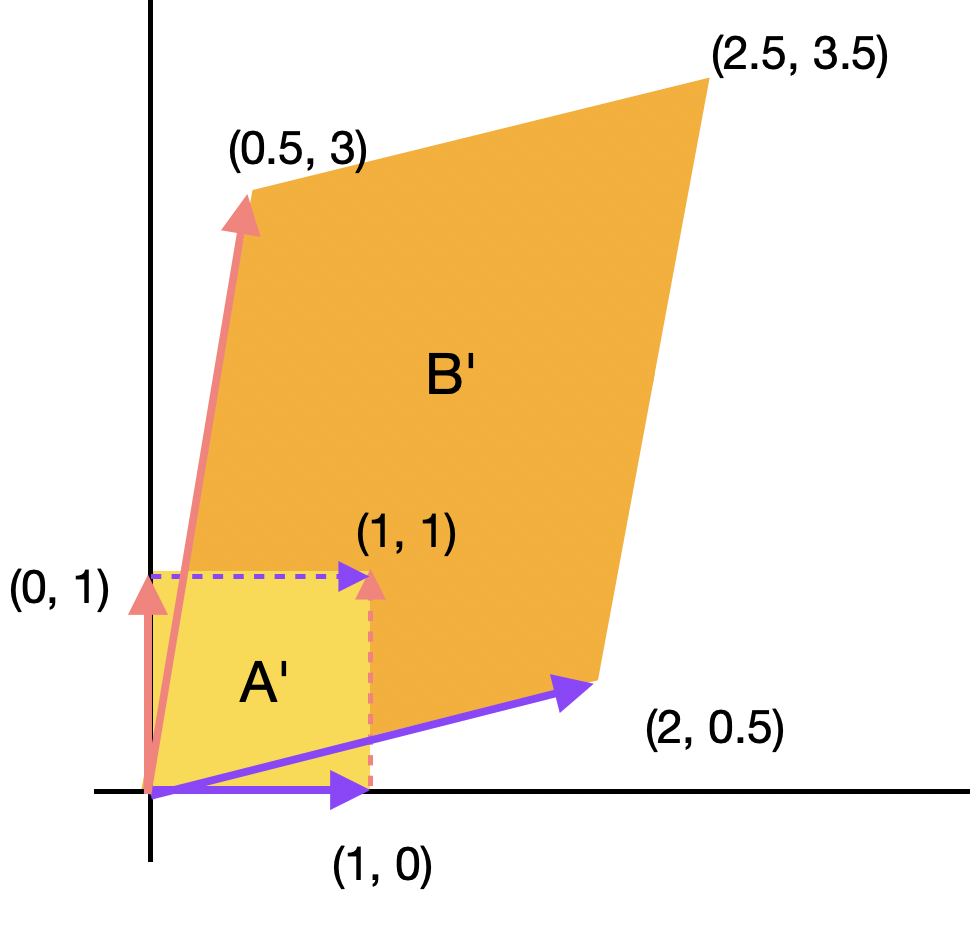
끝으로 행렬을 구성하는 칼럼 벡터 중 하나에 \(k\)를 곱하면 행렬식의 크기도 \(k\)배가 된다. 이는 넓이가 \(k\)배가 된다는 것을 통해 확인할 수 있다.
\[\eqalign{ &\det ( B ) = \det ( \begin{bmatrix} 3 && {1 \over 2} \\ {1 \over 2} && 2 \\ \end{bmatrix} ) = 5.75 \\ &\det ( B'' ) = \det ( \begin{bmatrix} 3 && 1 \\ {1 \over 2} && 4 \\ \end{bmatrix} ) = 11.5 \\ }\]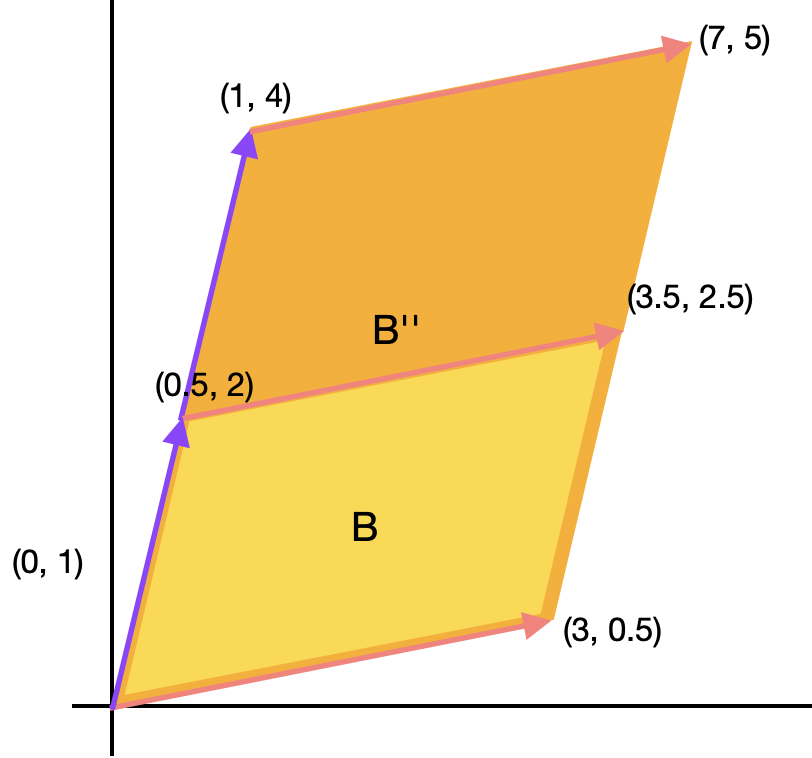
Properties of Determinant
행렬식의 특성을 다음과 같이 정리할 수 있다.
- 어떤 행렬의 행벡터 또는 열벡터 중 하나가 영벡터이면 행렬식의 값 또한 0이다.
- 어떤 행렬의 행벡터 또는 열벡터 중 하나에 \(k\)를 곱해준 행렬의 행렬식은 원 행렬의 행렬식에 \(k\)를 곱한 것과 같다.
- 어떤 행렬의 행렬식과 그것의 두 열의 위치를 바꾼 행렬의 행렬식은 크기는 같고 부호가 다르다.
- 어떤 행렬의 행렬식과 그것의 두 행의 위치를 바꾼 행렬의 행렬식은 크기는 같고 부호가 다르다.
- 어떤 행렬의 행렬식과 그것의 전치행렬의 행렬식은 동일하다.
Outper Product
외적(Outer Product)은 Cross Product, Vector Product라고도 하며, \(\times\)로 표기한다. 내적과 마찬가지로 벡터 간 연산이지만 스칼라 값을 반환하는 내적과는 달리 벡터 값을 반환한다. 그리고 두 2차원 벡터의 외적으로 얻은 벡터는 두 2차원 벡터 모두와 직교(Orthogonal)한다. 따라서 2차원의 두 벡터 외적을 표현하기 위해서는 3차원 공간이 필요하다. 두 3차원 벡터 \(\boldsymbol{u}, \boldsymbol{u}\)의 외적 \(\boldsymbol{u} \times \boldsymbol{v}\)는 다음과 같이 구할 수 있다. 이때 \(\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\)는 3차원 공간의 단위벡터들이다.
\[\eqalign{ & \boldsymbol{a} = \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ \end{bmatrix} \\ & \boldsymbol{b} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ \end{bmatrix} \\ &\eqalign{ \boldsymbol{a} \times \boldsymbol{b}&=\det ( \begin{bmatrix} \boldsymbol{i} & a_1 & b_1 \\ \boldsymbol{j} & a_2 & b_2 \\ \boldsymbol{k} & a_3 & b_3 \\ \end{bmatrix} ) \\ &=\det ( \begin{bmatrix} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ \end{bmatrix} ) \\ & = \det ( \begin{bmatrix} a_2 && a_3 \\ b_2 && b_3 \\ \end{bmatrix} ) \boldsymbol{i} - \det ( \begin{bmatrix} a_1 && a_3 \\ b_1 && b_3\\ \end{bmatrix} ) \boldsymbol{j} + \det ( \begin{bmatrix} a_1 && a_2 \\ b_1 && b_2\\ \end{bmatrix} ) \boldsymbol{k}}}\]외적이 무엇인지 알기 위해 행렬식을 먼저 본 이유가 보다 명확해졌다고 할 수 있다. 외적을 구하는 식은 \(3 \times 3\) 행렬의 행렬식을 구하는 식과 동일하다. 그렇다면 외적을 통해 구한 벡터 \(\boldsymbol{a} \times \boldsymbol{b}\)의 크기와 방향은 어떤 의미를 가질까.
Magnitude of Outer Product
간단히 정의하면 두 벡터의 외적의 크기는 두 벡터로 만들 수 있는 평행사변형의 넓이이다. 이때 아래와 같이 수식을 정리하여 보다 쉽게 그 크기를 구할 수 있다.
\[\eqalign{ \boldsymbol{a} \times \boldsymbol{b} & = \det ( \begin{bmatrix} a_2 && a_3 \\ b_2 && b_3 \\ \end{bmatrix} ) \boldsymbol{i} - \det ( \begin{bmatrix} a_1 && a_3 \\ b_1 && b_3\\ \end{bmatrix} ) \boldsymbol{j} + \det ( \begin{bmatrix} a_1 && a_2 \\ b_1 && b_2\\ \end{bmatrix} ) \boldsymbol{k} \\ \Rightarrow \| \boldsymbol{a} \times \boldsymbol{b} \| & = \det ( \begin{bmatrix} a_2 && a_3 \\ b_2 && b_3 \\ \end{bmatrix} )^2 + \det ( \begin{bmatrix} a_1 && a_3 \\ b_1 && b_3\\ \end{bmatrix} )^2 + \det ( \begin{bmatrix} a_1 && a_2 \\ b_1 && b_2\\ \end{bmatrix} )^2\\ &= (a_2 b_3 - b_2 a_3)^2 + (a_1 b_3 - b_1 a_3)^2 + (a_1 b_2 - b_1 a_2)^2\\ &= (a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) - (a_1 b_1 + a_2b_2 + a_3b_3)\\ &= \|a\|^2\|b\|^2 - \|a\|\|b\|\cos^2\theta \\ &= \|a\|^2\|b\|^2 \sin^2\theta \\ \therefore \| \boldsymbol{a} \times \boldsymbol{b} \| &= \|a\|^2\|b\|^2 \sin^2\theta }\]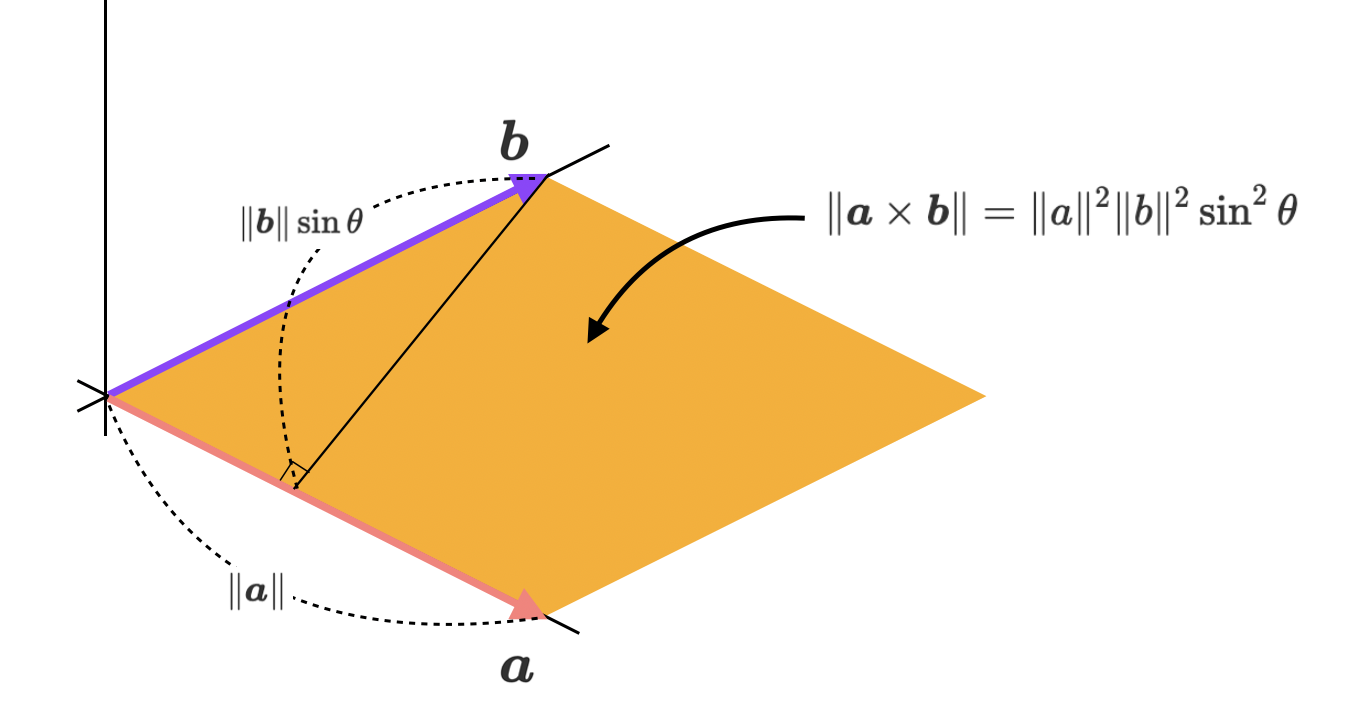
Direction of Outer Product
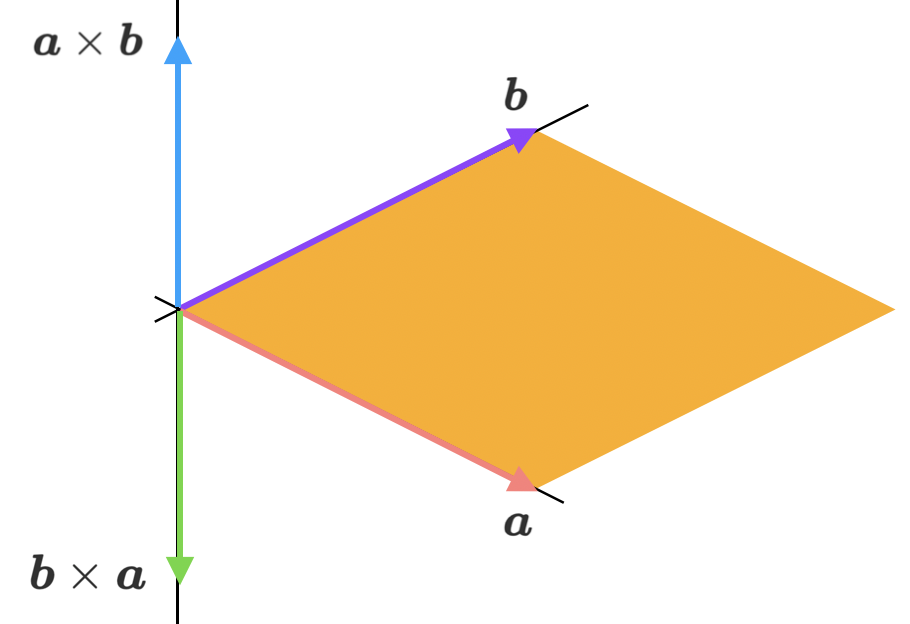
앞에서도 언급하였듯이 두 벡터의 외적의 방향은 두 벡터 모두와 직교한다. 그런데 문제가 있다면 3차원 공간에서 두 벡터와 직교하는 벡터는 두 방향으로 존재한다는 것이다. 그런데 두 벡터의 외적 또한 그 순서에 따라 두 종류가 있다. 즉 \(\boldsymbol{a}, \boldsymbol{b}\)의 외적은 \(\boldsymbol{a} \times \boldsymbol{b}\), \(\boldsymbol{b} \times \boldsymbol{a}\) 두 가지가 존재하고, 서로 반대 방향을 가리키게 된다.
\[\boldsymbol{a} \times \boldsymbol{b} = - \boldsymbol{b} \times \boldsymbol{a}\]이때 어느 방향이 \(\boldsymbol{a} \times \boldsymbol{b}\)인지 알기 위해 사용하는 것이 오른손의 법칙이다. 엄지와 검지, 중지를 서로 직교하도록 했을 때, 검지의 방향을 첫 번째 벡터 \(\boldsymbol{a}\)의 방향, 중지의 방향을 두 번쩨 벡터 \(\boldsymbol{b}\)의 방향이라고 한다면 엄지의 방향이 \(\boldsymbol{a} \times \boldsymbol{b}\)의 방향이 된다는 것이다.