SVD, Singular Value Decomposition

• Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book과 주재걸 교수님의 강의 인공지능을 위한 선형대수를 듣고 작성했습니다.
• update at : 2020.07.28

0. Summary

• SVD는 어떤 행렬 \(A\)를 \(A = U \Sigma V^T\)와 같이 분해하는 것이다.
• \(U, V\)는 칼럼 벡터들이 orthonormal 한 특성을 가지는 행렬이고 \(\Sigma\)는 대각 행렬이다.
• SVD 식을 \(AV = U \Sigma\)와 같이 표현하면, SVD는 서로 직교하는 \(V\)의 칼럼 벡터들을 \(A\)로 선형 변환했을 때 그 결과 또한 서로 직교하는 벡터들로 이뤄진 행렬 \(U \Sigma\)이 되는 경우를 찾는 것이라 할 수 있다.
• SVD의 \(U, \Sigma, V\)를 구하기 위해 \(AA^T, A^TA\)를 고유값 분해하여 얻은 결과를 이용한다. \(U, V\)는 고유 벡터로, \(\Sigma\)는 고유 값으로 구성한다.

1. Introduction

행렬을 분해하여 그 특성을 알아보는 방법으로 고유값 분해가 있었다. 하지만 고유값 분해는 대상이 되는 행렬이 정사각 행렬이어야 한다는 점과 같이 여러 제약 사항을 가지고 있다. Singular Value Decomposition은 고유값 분해와 마찬가지로 주어진 행렬을 분해하는 방법이다. 고유값 분해에 비해 다소 복잡하지만 제약 사항이 적다는 점에서 활용 가능성이 높다.

2. Singular Value Decomposition

특이값 분해는 직사각 행렬 \(A \in R^{m \times n}\)를 다음과 같이 분해한다.

\[A = U \Sigma V^T\]

이때 \(U \in R^{m \times m}\)와 \(V \in R^{n \times n}\)는 모두 정사각 행렬이며 모두 칼럼 벡터들이 서로 직교(orthnormal)한다는 특성을 갖는다. 그리고 \(\Sigma \in R^{m \times n}\)는 직사각 행렬로 대각 요소들을 제외한 다른 요소들이 모두 0인 행렬이 된다. 그리고 대각요소들은 크기가 큰 순서대로 정렬된다. 이를 그림으로 나타내면 다음과 같다.

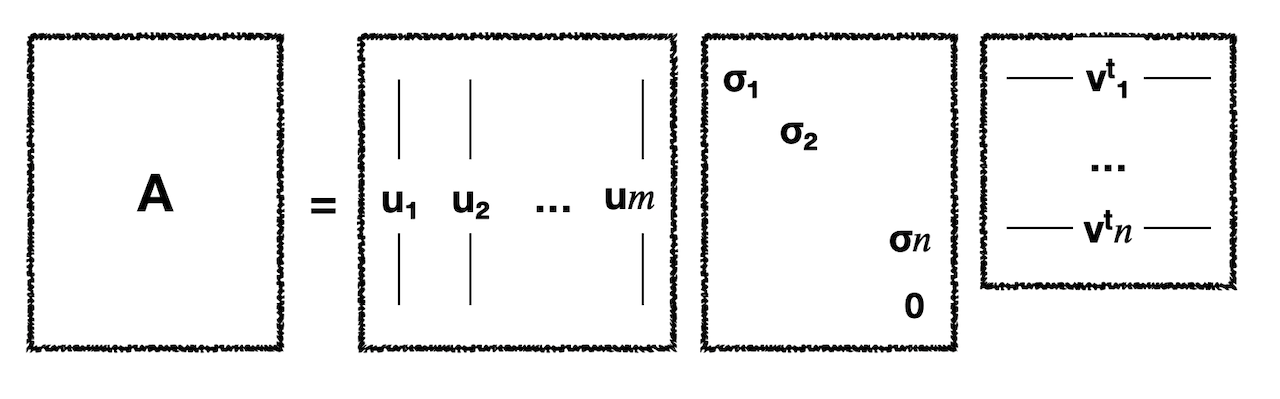
Relationship between \(A\) and \(U, V\)

여기서 \(\Sigma\)는 대각 요소를 제외한 모든 요소들이 0이다. 이 대각 요소를 계수(coefficient)로 본다면 \(U\)의 컬럼 벡터 중 \(n+1\)번째부터 \(m\)번째까지는 곱해져 0이 된다고 할 수 있다. 따라서 아래와 같이 줄여 표현하기도 하는데 이를 Reduced form of SVD라고 한다.

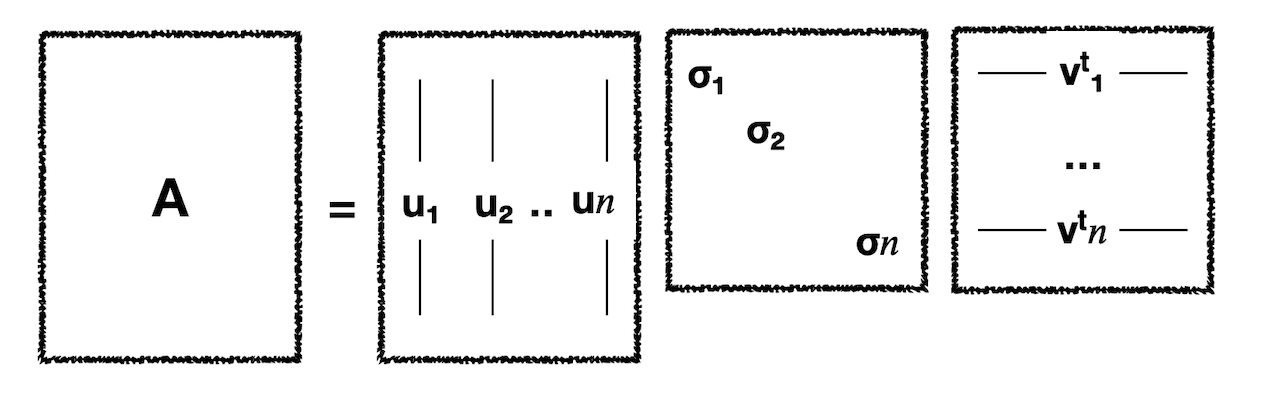
위의 그림에서 한 번 더 나아가 오른쪽 두 행렬을 곱해주면 다음과 같아진다.

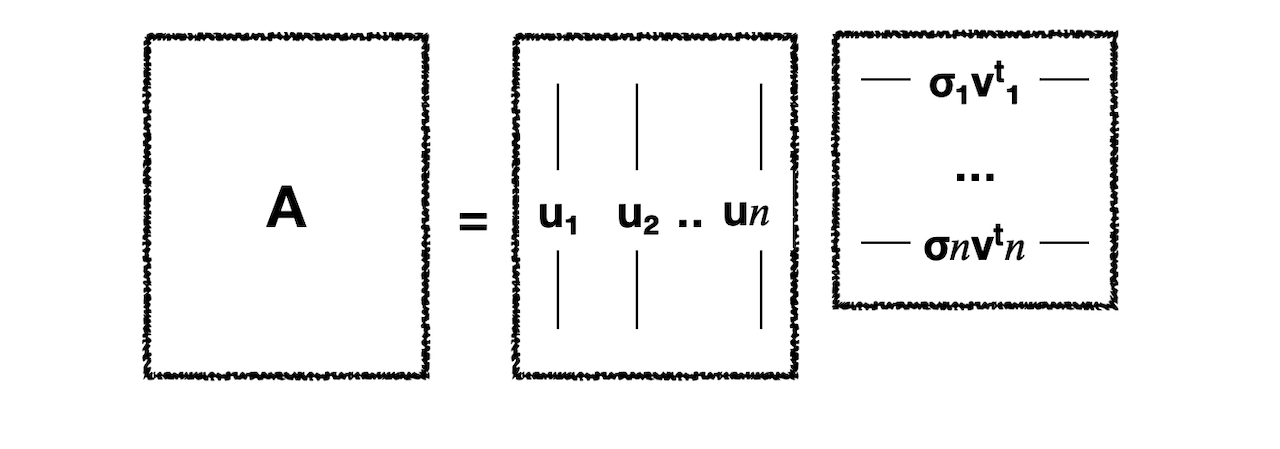
결과적으로 \(U\)의 컬럼 벡터의 선형 결합을 통해 \(A\)를 모두 표현할 수 있어야 한다는 것으로 이해할 수 있다. 그리고 반대로 \(A^{T} = V \Sigma^T U^T\)의 경우에도 동일하게 성립해야 하므로 \(V\)에 대해서도 동일한 조건이 적용된다.

SVD as Linear Transformation

SVD 식의 구조가 아닌 의미에 조금 더 집중해보자면 위의 SVD 식은 다음과 같이 전개해 볼 수 있다. 이때 \(U, V\)는 Orthonormal Matrix 이므로 역행렬과 전치 행렬이 같다(\(V^T = V^{-1}\)).

\[\eqalign{ & A = U \Sigma V^T \\ \rightarrow & A = U \Sigma V^{-1} \\ \rightarrow & AV = U \Sigma }\]

이를 분해하여 아래와 같이 벡터 간의 연산으로 나타낼 수 있다.

\[Av_1 = \sigma_1u_1 \\ Av_2 = \sigma_2u_2 \\ ... \\ Av_n = \sigma_n u_n \\\]

여기서 \(U, V\)의 칼럼 벡터들은 모두 서로 직교하므로 위 식은 서로 직교하는 벡터로 구성된 \(U\)에 \(A\)를 곱해주는 선형 변환의 결과 또 다른 차원에서 정의된 직교 벡터들을 얻을 수 있었다는 것을 의미하게 된다. 이는 반대로, 즉 \(V\)에 대해서도 동일하게 적용된다.

Summary

정리하자면 SVD는 다음과 같은 특성을 갖는다.

• \(A = U \Sigma V^T\)에서 \(U, V\)는 Orthogonal Matrix, \(\Sigma\)는 Diagonal Matrix 이다.
• 행렬 \(A\)는 \(U\)의 칼럼 벡터의 선형 결합으로, \(A^T\)는 \(V\)의 칼럼 벡터들의 선형 결합으로 표현할 수 있다.
• 어떤 직사각 행렬 \(A\)에 대해 \(U, \Sigma, V\)를 찾는다는 것은 어떤 Orthogonal Matrix를 \(A\)로 선형 변환했을 때 그 결과 또한 Orthogonal Matrix 인 경우를 찾는 것이라고 할 수 있다.

3. How To Get \(U, \Sigma, V\)

SVD를 구하는 것은 아래와 같이 \(A\)와 \(A^T\)를 곱하여 정방행렬로 만들고 이를 EigenDecomposition 하는 것에서 출발한다. 여기서 \(\Sigma\)는 대각 행렬이므로 \(\Sigma = \Sigma^T\)가 성립한다.

\[AA^T = U \Sigma V^T V \Sigma^T U^T = U\Sigma \Sigma^T U^T = U \Sigma^2 U^T \\ A^TA = V \Sigma U^T U \Sigma^T V^T = V\Sigma \Sigma^T V^T = V \Sigma^2 V^T\]

이렇게 하면 정방행렬 \(AA^T\) 을 \(U \Sigma^2 U^T\)로 분해한 것이 되고 이는 EigenDecomposition 식 \(VDV^{-1}\)과 매우 유사해진다. 하지만 이것이 EigenDecompostion과 완전히 동일해지기 위해서는 다음 세 가지 조건을 만족해야 한다. 다시 말해 아래 조건들을 만족한다면 EigenDecomposition을 통해 SVD를 수행할 수 있게 된다.

• \(AA^T, A^TA\)의 EigenVector들이 서로 모두 Orthonormal 해야 한다.
  • \(U, V\)는 Orthonoraml Matrix 이어야 하기 때문이다.
• 모든 EigenValue(\(\Sigma^2\)의 대각 요소)가 0 또는 양수여야 한다.
  • \(\Sigma\)의 요소들은 실수이기 때문이다.
• \(AA^T, A^TA\)의 EigenValue가 일치해야 한다.

결론부터 말하자면 대칭성(Symmetric)을 가지면서 Positive Definite한 특성을 가지는 \(AA^T와 A^TA\)는 항상 위 조건들을 만족한다.

Symmetric Matrix

대칭행렬이란 다음과 같이 원 행렬과 전치 행렬이 동일한 경우를 말한다.

\[A = A^T\]

이에 따르면 \(AA^T, A^TA\)는 대칭행렬이라고 할 수 있다.

\[(AA^T)^T = (A^T)^T (A)^T = AA^T\]

여기서 대칭성 여부가 중요한 이유는 대칭행렬는 항상 칼럼 벡터 간에 직교한다는 성질을 가지기 때문이다. 즉 \(n \times n\)의 대칭행렬는 n개의 선형 독립의 eigenvector을 가지고 동시에 모두 수직이라고 할 수 있다.

Positive Definite Matrix

Positive Definite란 양수 범위에서 정의되는 것을 말한다. 예를 들어 \(y = x^2 + 3\)은 \(x\)에 어떤 값을 대입하더라도 \(y\)값은 양수의 범위에서만 정의될 수 있다. 이러한 경우를 Positive Definite라고 한다. 0과 양수 범위에서 정의되는 경우에는 Positive Semi Definite라고 한다.

그렇다면 행렬이 Positive Definite 하다는 것은 무엇을 의미할까. 행렬이 Positive Definite하다는 것은 영 벡터가 아닌 어떤 벡터 \(\boldsymbol{x}\)에 대해 다음과 같은 식을 만족하는 경우를 말한다.

\[\boldsymbol{x^T A x} > 0\]

그리고 \(AA^T, A^TA\)는 다음과 같이 Positive Semi Definte 하다.

\[x^TAA^Tx = (A^Tx)^T(A^Tx) = | A^Tx |^2 \geqq 0 \\ x^TA^TAx = (Ax)^T(Ax) = | Ax |^2 \geqq 0\]

이러한 Positive Semi Definte Matrix는 Eigen Value가 항상 0보다 크거나 같다는 특성을 가진다. 따라서 \(AA^T, A^TA\)의 Eigen Value 또한 항상 0보다 크거나 같다고 할 수 있다.

Symmetric Positive Definite Matrix

다시 SVD가 가능한 조건들을 다시 살펴보면

• \(AA^T, A^TA\)의 EigenVector들이 서로 모두 Orthonormal 해야 한다.
  • \(AA^T, A^TA\)는 대칭행렬이므로 \(n\)개의 서로 직교하는 EigenVector를 가진다.
• 모든 EigenValue(\(\Sigma^2\)의 대각 요소)가 0 또는 양수여야 한다.
  • Positive Semi Definite한 특성을 가지는 \(AA^T, A^TA\)의 Eigen Value는 항상 0보다 크거나 같다.
• \(AA^T, A^TA\)의 EigenValue가 일치해야 한다.
  • \(U \Sigma^2 U^T\)에서 \(\Sigma^2\)와 \(V \Sigma^2 V^T\)에서 \(\Sigma^2\)는 일치한다.

와 같이 Symmetric Positive Definite Matrix \(AA^T, A^TA\)에서는 모두 만족하는 것을 확인할 수 있다.

정리하자면 대칭성을 가지면서 Positive Definite한 행렬 \(\boldsymbol{AA^T}\)에 대해 EigenDecomposition을 수행하게 되면 다음과 같은 식이 도출되고, 이것이 SVD \(A = U \Sigma V^T\)의 \(U\)가 된다. 똑같은 과정을 \(A^TA\)에 대해 수행하면 \(V\)도 구할 수 있다.

\[\eqalign{ \boldsymbol{AA^T} &= \boldsymbol{UDU^T} \\ & = [\boldsymbol{u_1 u_2 ... u_n}] \begin{bmatrix} \lambda_1 && 0 && ... && 0 \\ 0 && \lambda_2 && ... && 0 \\ ... && ... && ... && ... \\ 0 && 0 && ... && \lambda_n \\ \end{bmatrix} \begin{bmatrix} \boldsymbol{u_1^T}\\ \boldsymbol{u_2^T}\\ ...\\ \boldsymbol{u_n^T}\\ \end{bmatrix} \\ & = \lambda_1\boldsymbol{u_1 u_1^T} + \lambda_2\boldsymbol{u_2 u_2^T} + ... + \lambda_n\boldsymbol{u_n u_n^T} }\]

여기서 Positive Definite한 특성 때문에 모든 \(\lambda\) 값이 양수가 된다. 따라서 대칭행렬 \(\boldsymbol{AA^T}\)는 각 \(\boldsymbol{u_iu_i^T}\)가 \(\lambda_i\)의 비율만큼 합쳐진 것이 된다. 이때 \(\lambda_i\)가 큰 순서대로 정렬되어 있다면 \(\boldsymbol{u_1} > \boldsymbol{u_2} > ... > \boldsymbol{u_n}\)의 순서로 중요하다고 할 수 있다.

Summary

SVD의 계산과 관련해서 다음과 같이 정리할 수 있다.

• EigenDecompostion과 달리 직사각 행렬에 대해 SVD는 항상 가능하다.
• 정사각 행렬 중 대칭성을 가지면서 Positive Definite한 특성을 가진다면 Eigen Decomposition의 결과와 SVD의 결과가 일치한다.