EigenDecomposition
- Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book과 주재걸 교수님의 강의 인공지능을 위한 선형대수를 듣고 작성했습니다.
- update at : 2020.07.18
1. EigenValue & EigenVector
고유값 분해(EigenDecomposition)는 주어진 행렬의 특성을 찾아내기 위해 사용하는 방법 중 하나이다. 고유값 분해를 이해하기 위해서는 고유벡터와 고유값에 대해서 먼저 알야야 하는데, 고유벡터(EigenVector)는 어떤 행렬의 곱에 의한 선형 변환으로 방향이 변화하지 않는 특이한 성질을 가지는 벡터를 말한다. 고유벡터를 구하기 위해서는 주어진 행렬이 정방행렬이어야 하며 다음과 같은 공식을 만족해야 한다.
\[\boldsymbol{A}\boldsymbol{x} = \lambda\boldsymbol{x}\]여기서 \(\boldsymbol{v}\)가 고유벡터가 되고 \(\lambda\)가 고유값이 된다. 위의 식에서 한 가지 유추해 볼 수 있는 것은 행렬 \(\boldsymbol{A}\)를 곱해주는 선형 변환의 결과로 \(\boldsymbol{x}\)의 크기는 \(\lambda\)만큼 바뀌었지만 그 방향은 변하지 않는다는 것이다. 즉 어떤 행렬의 고유벡터란 해당 행렬을 곱하더라도 방향이 변하지 않는 벡터를 말한다고 할 수 있다.
EigenVector and Linear Dependence
그렇다면 행렬 \(\boldsymbol{A}\)가 있을 때 행렬의 고유벡터와 고유값은 어떻게 알 수 있을까. 이를 위해 위의 식을 아래와 같이 전개해 볼 수 있다.
\[\eqalign{ & \boldsymbol{A}\boldsymbol{x} - \lambda\boldsymbol{x} = \boldsymbol{0} \\ \rightarrow & \boldsymbol{A}\boldsymbol{x} - \lambda\boldsymbol{I}\boldsymbol{x} = \boldsymbol{0}\\ \rightarrow & ( \boldsymbol{A} - \lambda\boldsymbol{I} ) \boldsymbol{x} = \boldsymbol{0}\\ }\]위의 식을 만족하는 가장 쉬운 해는 \(\boldsymbol{x}\)가 \(\boldsymbol{0}\)인 경우(trivial solution)일 것이다. 하지만 고유 벡터가 0인 경우는 의미가 없기 때문에 일반적으로 고려하지 않는다. 그런데 \(\boldsymbol{x} \neq \boldsymbol{0}\)와 \(( \boldsymbol{A} - \lambda\boldsymbol{I} ) \boldsymbol{x} = \boldsymbol{0}\)를 동시에 만족하기 위해서는 \(( \boldsymbol{A} - \lambda\boldsymbol{I} )\)가 선형 의존이어야 한다. \(( \boldsymbol{A} - \lambda\boldsymbol{I} )\)이 선형 독립이라는 것은 각 칼럼 벡터가 다른 칼럼 벡터로는 줄일 수 없는 차원 축을 가지고 있다는 것을 의미하는데 이렇게 되면 \(\boldsymbol{x} = 0\)인 경우에만 가능하기 때문이다.
역행렬의 유무와 관련지어 생각해보면 판별식 \(det ( \boldsymbol{A} - \lambda\boldsymbol{I} ) \neq 0\)인 경우, 즉 역행렬이 있는 경우라면 가능한 \(\boldsymbol{x}\)가 단 하나 밖에 없다는 것을 의미하는데 우리는 이미 그 하나의 해가 \(\boldsymbol{x} = \boldsymbol{0}\)이라는 것을 알고 있다. 따라서 역행렬이 존재하는 경우는 의미가 없다. 반면 \(det ( \boldsymbol{A} - \lambda\boldsymbol{I} ) = 0\) 이라면 해가 없거나 무수히 많다는 것을 의미하고 \(\boldsymbol{x} = \boldsymbol{0}\)라는 해를 알고 있으므로 결과적으로 해는 무수히 많다고 할 수 있다. 이를 종합해보면 역행렬이 존재하지 않는 경우에만 \(\boldsymbol{x}=\boldsymbol{0}\)외에 다른 해가 존재하게 된다.
정방행렬에서는
- 선형의존과 역행렬의 있다는 동치이다.
- 선형독립과 역행렬이 없다는 동치이다.
가 성립하므로 \(\boldsymbol{A}\)가 선형 독립이라면 \(\lambda\boldsymbol{I}\)를 잘 결정하여 \(( \boldsymbol{A} - \lambda\boldsymbol{I} )\)는 선형 의존이 되도록 하여야 한다. 혹은 \(det ( \boldsymbol{A} - \lambda\boldsymbol{I} ) = 0\)이 성립하여야 한다.
EigenVector and Null Space
어떤 행렬 \(\boldsymbol{A}\)의 Null Space \(\text{Nul}\boldsymbol{A}\)는 \(\boldsymbol{A}\boldsymbol{x} = \boldsymbol{0}\)을 만족하는 \(\boldsymbol{x}\)의 집합을 의미한다. 이를 위의 식에 적용하면 \(\text{Nul}( \boldsymbol{A} - \lambda\boldsymbol{I} )\)는 곧 가능한 고유 벡터 \(\boldsymbol{x}\)의 집합이 된다.
\[\begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22}\\ a_{31} && a_{32}\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 0\\ \end{bmatrix}\]위의 식에서 행렬 \(\boldsymbol{A}\)의 Null space는 위 식을 만족하는 \(x_1, x_2\)의 조합이라고 할 수 있다. 그런데 위의 식은 row 별로 분해하여 다음과 같아 나타낼 수 있다.
\[\begin{bmatrix} a_{11} && a_{12} \end{bmatrix} \cdot \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = 0 \\ \begin{bmatrix} a_{21} && a_{22} \end{bmatrix} \cdot \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = 0 \\ \begin{bmatrix} a_{31} && a_{32} \end{bmatrix} \cdot \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = 0 \\\]벡터 간의 내적은 두 벡터가 수직인 경우에만 0이 되므로, 위의 세 식을 모두 만족하기 위해서는 벡터 \(x\)가 \(\boldsymbol{A}\)의 모든 row 벡터들과 수직이어야 한다. 정리하자면 \(\text{Nul}\boldsymbol{A}\)는 \(\boldsymbol{A}\)의 모든 row 벡터들과 수직인 벡터들의 집합이라고 할 수 있다. 그리고 \(( \boldsymbol{A} - \lambda\boldsymbol{I} )\)의 row 벡터들과 모두 수직인 \(\boldsymbol{x}\)가 \(\boldsymbol{A}\)의 고유벡터가 된다.
Null Space와 관련하여 한 가지 짚고 넘어갈 것이 있다면 Null Space는 전체 벡터 공간 \(R^n\)의 subspace로서 Row Space와 차원의 합이 전체 벡터 공간의 차원 \(n\)과 항상 같다는 것이다.
\[\text{dim} \ n = \text{dim} \ \text{Row}A + \text{dim} \ \text{Nul}A\]Characteristic Equation and Eigen Space
특성 방정식(Characteristic Eqation)은 다음과 같이 정의되며 \(\boldsymbol{A}\)의 고유값 \(\lambda\)를 구하기 위해 사용된다.
\[det (\boldsymbol{A} - \lambda \boldsymbol{I}) = 0\]이를 만족하는 고유값 \(\lambda_i\)에 따라 \(\text{Nul}(\boldsymbol{A} - \lambda_i \boldsymbol{I})\)가 달리 정의되므로 고유값에 따라 고유벡터가 달라진다고 할 수 있다. 그리고 전체 3차원 공간 속에서 Row Space가 1차원인 경우 Null Space는 2차원이 되며 이렇게 되면 평면 상의 모든 벡터들이 고유 벡터가 된다. 따라서 하나의 고유값에 대해 복수의 고유 벡터가 존재할 수 있다. 참고로 고유 벡터가 정의되는 공간을 고유값 \(\lambda_i\)의 Eigen Space라고 한다.
Summary: How to get EigenVector
고유 벡터를 구하기 위해서는 아래와 같은 조건들이 붙으며 따라서 제한적인 상황에서만 구할 수 있다.
- \(\boldsymbol{A}\)는 정방행렬이어야 한다.
- \(det (\boldsymbol{A} - \lambda \boldsymbol{I}) = 0\)를 만족하는 \(\lambda\)를 찾을 수 있어야 한다.
고유값과 고유벡터를 구하는 과정은 다음 두 단계로 나눌 수 있다.
- 특성 방정식 \(det (\boldsymbol{A} - \lambda \boldsymbol{I}) = 0\)에 따라 가능한 \(\lambda\)를 찾는다.
- 각각의 \(\lambda\)에 따라 고유벡터가 존재하는 공간 EigenSpace를 찾는다.
2. Diagonalization
대각 행렬(Diagonal Matrix)이란 아래와 같이 대각 요소를 제외한 나머지 요소들이 모두 0인 행렬을 말한다.
\[\begin{bmatrix} a_1 && 0 && ... && 0 && 0 \\ 0 && a_2 && ... && 0 && 0 \\ ... && ... && ...&& ... && ... \\ 0 && 0 && ... && a_{k-1} && 0 \\ 0 && 0 && ... && 0 && a_k \\ \end{bmatrix}\]대각화(Diagonalization)란 주어진 행렬을 대각 행렬로 만드는 것이다. 항상 가능한 것은 아니지만 다음과 같이 행렬 \(\boldsymbol{A}\)의 앞뒤로 행렬 \(\boldsymbol{V}\)와 그 역행렬 \(\boldsymbol{V}^{-1}\)을 곱해주는 것으로 대각 행렬 \(\boldsymbol{D}\)를 구할 수 있다.
\[\boldsymbol{D} = \boldsymbol{V}^{-1} \boldsymbol{A} \boldsymbol{V}\]여기서 \(\boldsymbol{D}\)는 대각행렬이므로 \(\boldsymbol{VD}\)는 다음과 같이 \(\boldsymbol{V}\)의 칼럼 벡터들의 합으로 표현할 수 있다.
\[\eqalign{ \boldsymbol{VD} & = \begin{bmatrix} \boldsymbol{v_1} &&\boldsymbol{v_2} && ... &&\boldsymbol{v_k} \end{bmatrix} \begin{bmatrix} a_1 && ... && 0 \\ ... && ...&& ... \\ 0 && ... && a_k \\ \end{bmatrix} & = \begin{bmatrix} a_1 \boldsymbol{v_1} && ... && a_k \boldsymbol{v_k} \end{bmatrix} }\]따라서 전체 식은 다음과 같이 표현할 수 있다.
\[\boldsymbol{V} \boldsymbol{D} = \boldsymbol{A} \boldsymbol{V} \qquad \Rightarrow \qquad \begin{bmatrix} a_1 \boldsymbol{v_1} && ... && a_k \boldsymbol{v_k} \end{bmatrix} = \begin{bmatrix} \boldsymbol{A} \boldsymbol{v_1} && ... && \boldsymbol{A} \boldsymbol{v_k} \end{bmatrix}\]위 식에서 대각행렬의 대각요소 \(a\)를 고유 값으로, \(\boldsymbol{v_i}\)를 고유 벡터로 본다면 다음과 같이 여러 개의 고유 벡터 식이 된다는 것을 알 수 있다.
Diagonalizable?
앞서 언급한 것과 같이 항상 위와 같은 방법으로 행렬의 대각화가 가능한 것은 아니다. 대각화가 가능하기 위해서는 다음 조건을 만족해야 한다.
- \(\boldsymbol{V}\)는 역행렬을 가져야 한다.
- \(\boldsymbol{V}\)는 정방행렬이어야 한다.
- \(\boldsymbol{V}\)는 선형 독립의 column들을 가져야 한다.
3. EigenDecomposition
만약 위와 같이 대각요소 \(a\)를 고유 값으로, \(\boldsymbol{v_i}\)를 고유 벡터로 본다면 행렬 \(\boldsymbol{A}\)는 \(k\)개의 고유 벡터를 가져야 한다는 조건이 추가될 것이며 이때 대각 행렬 \(\boldsymbol{D}\)의 대각 요소 \(a_k\)에는 각 고유 벡터에 맞는 고유 값이 들어가게 될 것이다.
이때 위의 대각 행렬 식을 \(\boldsymbol{A}\)에 대한 식으로 바꾸면 다음과 같이 나타낼 수 있는데, 이를 고유값 분해(EigenDecomposition)라고 한다. 참고로 Decomposition이란 하나의 행렬을 여러 행렬 간의 곱으로 나타내는 것으로 이해할 수 있다.
\[\boldsymbol{A} = \boldsymbol{V} \boldsymbol{D} \boldsymbol{V}^{-1}\]Meaning of EigenDecomposition
어떤 행렬 \(\boldsymbol{A}\)가 있고 대각화가 가능하여 \(\boldsymbol{A} = \boldsymbol{V} \boldsymbol{D} \boldsymbol{V}^{-1}\)이 성립한다고 하자. 이때 행렬 \(\boldsymbol{A}\)를 곱하여 벡터 \(\boldsymbol{x}\)를 선형 변환하는 것은 다음과 같이 나타낼 수 있다.
\[\boldsymbol{A}\boldsymbol{x} = \boldsymbol{V} \boldsymbol{D} \boldsymbol{V}^{-1} \boldsymbol{x}\]이는 \(\boldsymbol{x}\)에 \(\boldsymbol{A}\)를 곱해 선형 변환을 1번 하는 것과 \(\boldsymbol{V}^{-1}, \boldsymbol{D}, \boldsymbol{V}\)를 차례대로 곱해주어 3번의 선형 변환을 하는 것의 목적지는 동일하다는 것을 의미한다.
1) Linear Transformation with \(V^{-1}\)
\[\boldsymbol{V}\boldsymbol{a} = \boldsymbol{b}\]위와 같은 선형 결합은 주어진 벡터를 행렬의 \(\text{Col}\boldsymbol{V}\)에 매핑하는 것이다. 만약 역으로 \(\text{Col}\boldsymbol{V}\)가 결정되어 있고 이를 통해 처음 주어진 벡터를 구하는 문제가 있다면 칼럼 벡터 \(\boldsymbol{v_1}, \boldsymbol{v_2}\)를 얼마나 사용하여 목적지 \(\boldsymbol b\)를 표현할 것인지 찾는 것과 같은 문제가 된다. 예를 들어 \(\begin{bmatrix} 1 && 1 \\ 1 && -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 3 \\ 1 \end{bmatrix}\)에서 \(x_1, x_2\)는 각 칼럼 벡터를 얼마나 사용할 것인지를 의미한다. \(x_1 = 2, x_2 = 1\)라면 1번 칼럼 벡터 \(\boldsymbol{v_1}\)를 2번 더한 것에 \(\boldsymbol{v_2}\)를 1번 더한 것과 같다는 것으로, 다음과 같은 그림으로 표현할 수 있다.
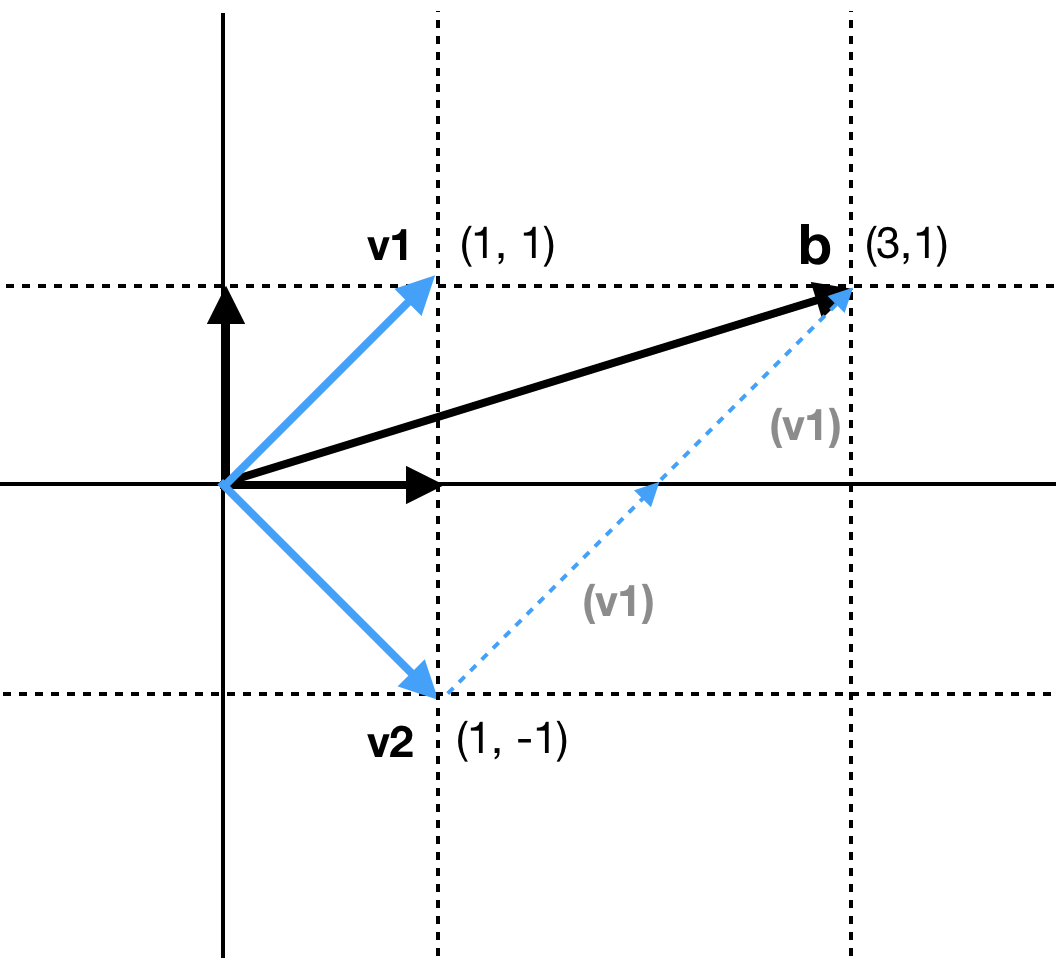
그런데 위 식은 다음과 같이 표현할 수 있다.
\[\boldsymbol{a} = \boldsymbol{V}^{-1} \boldsymbol{b}\]여기서 \(\boldsymbol{a}\)는 \(\boldsymbol{V}\)의 칼럼 벡터를 얼마나 사용할 것인지를 의미한다고 했었다. 만약 \(\boldsymbol{V}\)가 \(\boldsymbol{A}\)의 고유 벡터들로 구성되어 있다면 위 식을 통해 각 고유 벡터를 얼마나 사용할 것인가를 구할 수 있게 된다.
따라서 \(\boldsymbol{V}^{-1} \boldsymbol{x}\)는 원 벡터 \(\boldsymbol{x}\)를 \(\boldsymbol{A}\)의 고유벡터로 나타낸다고 할 때 각 고유벡터가 필요한 정도를 나타낸다.
2) Linear Transformation with \(D\)
\(\boldsymbol{D}\)는 대각 행렬이며 각 대각 행렬의 요소가 고유 값을 의미한다고 했었다. 따라서 \(\boldsymbol{V}^{-1}\boldsymbol{x}\)에 \(\boldsymbol{D}\)를 곱하는 것은 각 고유 벡터를 얼마나 사용할 것인지 알려주는 계수에 각 고유 벡터의 고유 값을 곱해주는 것이 된다.
3) Linear Transformation with \(V\)
고유값 분해 식의 마지막 과정은 \(\boldsymbol{D}\boldsymbol{V}^{-1}\boldsymbol{x}\)에 \(\boldsymbol{V}\)로 한 번 더 선형 변환 해주는 것이다. 앞의 두 단계는 차례대로 1. 각 고유 벡터를 얼마나 사용할 것인지 2. 각 고유 벡터의 고유값은 어떻게 되는지 확인하는 과정이었다. 이때 여기에 고유 벡터를 곱해주면 \(\boldsymbol{A}\)에 의한 선형 변환의 결과를 나타낼 수 있게 된다. \(\boldsymbol{V}\)를 곱해주는 것이 바로 고유 벡터를 곱해주는 것을 의미한다고 할 수 있다.
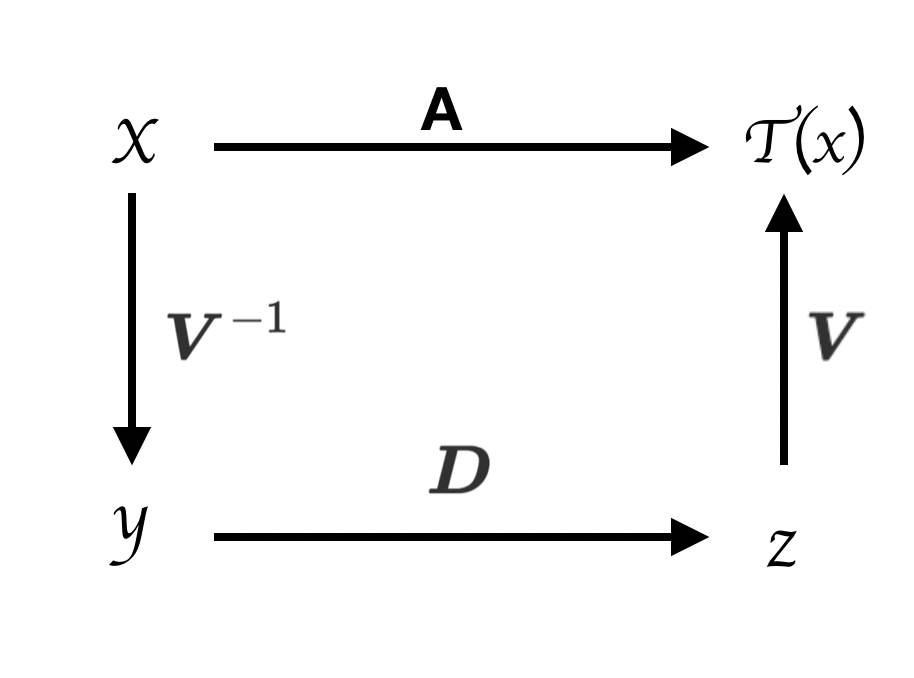
정리하자면 목표는 \(\boldsymbol{A}\boldsymbol{x} = \boldsymbol{V} \boldsymbol{D} \boldsymbol{V}^{-1}\boldsymbol{x}\)이 성립하도록 하는 것으로, 좌변의 하나의 선형 변환 결과와 우변의 세 번의 선형 변환 결과가 동일하도록 하는 것이었다. 여기서 \(\boldsymbol{A}\)의 고유 벡터는 \(\boldsymbol{A}\)에 의해 선형 변환 되어도 방향은 유지하는 벡터를 의미하고, 이는 곧 \(\text{Col}\boldsymbol{A}\)의 기저 벡터로 \(\boldsymbol{A}\)의 고유 벡터들이 사용될 수 있음을 의미하게 된다. 즉 \(\boldsymbol{A}\boldsymbol{x}\)는 \(\boldsymbol{A}\)의 기저 벡터들의 선형 결합으로 나타낼 수 있다는 것이다. 이를 위해서 고유 벡터에 고유 값을 곱해주고 각각의 고유 벡터가 얼마나 사용되는지 알아내어 곱해주는 과정이 필요한 것이다. 따라서 위 식 \(\boldsymbol{V} \boldsymbol{D} \boldsymbol{V}^{-1}\boldsymbol{x}\)의 의미는 다음과 같이 정리할 수 있다.
- \(\boldsymbol{V}\) : 고유벡터로 표현하기
- \(\boldsymbol{D}\) : 각 고유벡터의 고유값 곱해주기
- \(\boldsymbol{V}^{-1}\) : 각 고유벡터가 사용되는 크기에 따라 계수 곱해주기
Repeated Multiplication with EigenDecomposition
행렬 \(\boldsymbol{A}\)를 반복적으로 곱해주어야 하는 경우 고유값 분해를 사용하면 연산량을 크게 줄일 수 있다.
\[\boldsymbol{A}^{k} = \boldsymbol{V} \boldsymbol{D}^{k} \boldsymbol{V}^{-1}\]