Orthogonality

• Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book과 주재걸 교수님의 강의 인공지능을 위한 선형대수를 듣고 작성했습니다.
• update at : 2020.07.15

Orthogonal Set

Orthogonal Set이란 말 그대로 서로 직교하는 벡터들의 집합을 말한다. 즉 Orthogonal Set의 모든 벡터들은 정의된 공간 내에서 서로 직교하고 따라서 서로 내적을 했을 때 그 값이 0이 된다. 직교성은 선형 독립보다 강력한(strict) 조건이므로 Orthogonal Set의 벡터들은 선형 독립의 특성을 가진다.

Orthogonal Projection

직교하지 않는 벡터들이 주어졌을 때 기존 벡터의 특성은 최대한 유지하되 서로 직교하도록 만드는 방법을 다음 그림과 같이 2차원 벡터 공간에서 생각해 볼 수 있다.

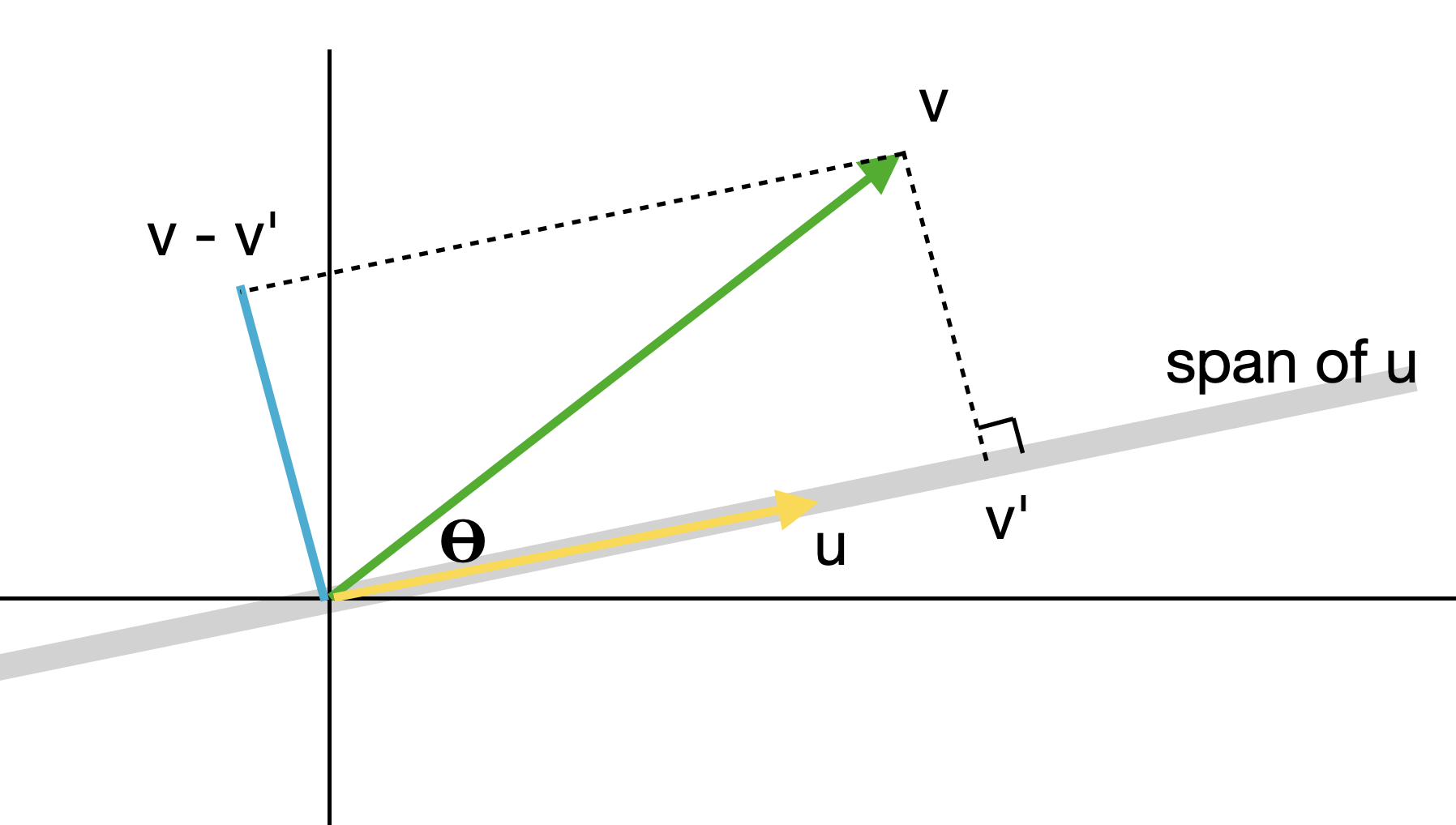
위의 그림은 서로 직교하지 않는 두 벡터 \(u, v\) 중 \(v\)를 \(u\)에 수선의 발을 내려(orthogonal projection) \(v\)의 특성 중 \(u\)와 직교하는 특성만 남긴 새로운 벡터 \(u - v'\)를 구하는 것을 보여주는 그래프이다. 구체적인 과정은 아래와 같다.

• 벡터 \(v\)에서 벡터 \(u\)의 span으로 수선의 발을 내린다. 원점에서 수선의 발까지의 벡터를 \(v'\)이라고 하며 당연히 \(u\)의 span 상에 포함되는 벡터이다.
• 두 벡터 \(u, v\)가 이루는 각도를 \(\theta\)로 가정하면 \(v'\)의 길이를 다음과 같이 정의할 수 있다.

\[\| v' \| = \| u \| \cos \theta\]

• 이때 두 벡터 \(u, v\)의 내적은 다음과 같다.

\[u \cdot v = \| u \| \cdot \| v \| \cos \theta \\\]

• 따라서 두 번째 식과 같이 \(v'\)의 길이를 구할 수 있다.

\[\| v' \| = \| u \| \cos \theta = {u \cdot v \over \| u \|}\]

• \(v'\)의 길이를 구했다면 \(v'\)의 방향을 나타내는 단위 벡터를 구하여 곱해주면 \(v'\) 자체를 구할 수 있다. \(v'\)는 \(u\)의 span 상에 존재하므로 \(v'\)의 방향과 \(u\)의 방향은 동일하다고 할 수 있으며 단위 벡터로 normalize 한 결과 또한 동일하다고 할 수 있다. 따라서 \(u\)의 단위 벡터를 사용하여 \(y'\)를 다음과 같이 구할 수 있다.

\[u' = {u \cdot v \over \| u \|} {u \over \| u \|} = {u \cdot v \over \| u \|^2} u = {u \cdot v \over u \cdot u} u\]

• \(v'\)를 구했다면 이를 원벡터 \(v\)에 빼주어 \(v - v'\)를 쉽게 구할 수 있다.

3차원 이상의 공간에서도 직선이 아닌 평면, 그 이상의 공간에 수선의 발을 내린다는 점 외에 비슷한 방법으로 벡터들을 직교하도록 만들어 줄 수 있다.

Gram-Schmidt Process

Gram-Schmidt Process는 어떤 벡터 공간 내의 벡터 집합이 주어져 있을 때 벡터 집합의 모든 벡터들을 표현할 수 있는 직교 벡터들을 구하는 과정이라고 할 수 있다. 이를 위해 위에서 살펴본 Orthogonal Projection을 사용하게 된다. 여기서 \(u\)는 주어진 벡터 집합, 즉 표현 대상이라고 할 수 있고 \(v\)는 \(u\)를 표현하기 위해 필요한 직교 기저 벡터들이라고 할 수 있다. 그리고 \(\text{Proj}_{u}(v)\)는 벡터 \(u\)에 \(v\)를 orthogonal projection 한 결과 \(v'\)를 의미한다.

\[\eqalign{ &u_1 = v_1 \\ &u_2 = v_2 - \text{Proj}_{u_1} (v_2)\\ &u_3 = v_3 - \text{Proj}_{u_1} (v_3) - \text{Proj}_{u_2} (v_3)\\ & ...\\ &u_k = v_k - \Sigma_{i=1}^{k-1}\text{Proj}_{u_i}(v_k) }\]

위의 수식을 보게 되면 \(u_1\)을 표현하기 위해 \(v_1\) 하나만 사용하고, 다음 벡터 \(u_2\)를 표현하기 위해서는 \(v_2\)와 더불어 \(u_1\)을 함께 사용한다. 이후 다음 벡터를 표현하려 할 때마다 새로운 직교 벡터 \(v_k\)와 \(v_k\)를 이전 모든 \(u_1 \backsim u_{k-1}\)에 orghogonal projection 한 벡터를 빼주는 식으로 진행된다. 이러한 과정을 Matrix 간의 곱으로 표현할 수 있는데 이를 QR Factorizaton 이라고 한다.