Least Square Problem

• Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book과 주재걸 교수님의 강의 인공지능을 위한 선형대수를 듣고 작성했습니다.
• update at : 2020.07.14

Introduction

대부분의 머신러닝 문제에서는 feature의 수보다 data의 개수가 더 많다. 이를 선형 방정식 \(\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}\)로 표현한다면 행렬 \(\boldsymbol{A}\)는 row보다 column이 작은 직사각형 행렬이 되며 이 경우 정확한 해를 구하는 것이 매우 어려워진다. 따라서 이러한 문제를 풀기 위해서는 정확한 \(\boldsymbol{x}\)를 구하는 것이 아닌, \(\boldsymbol{x}\)에 최대한 근사(approximate)하는 값을 찾는 것이 현실적이다. 이것의 대표적인 방법이 Least Square이다.

Squared Error

Least Squares는 말 그대로 Squared Error의 크기를 최소화하는 것이다. 두 백터 \(\boldsymbol{A}\boldsymbol{x}\)와 \(\boldsymbol{b}\)를 최대한 최대한 가깝게 하는 \(\boldsymbol{x}\)를 찾으려 한다면 먼저 \(\boldsymbol{A}\boldsymbol{x}\)와 \(\boldsymbol{b}\) 간의 차이를 정의해야 할 것이다. Square Error는 다음과 같이 두 벡터 간 차이의 Norm을 사용하는 방법이다.

\[\hat x = \arg \min_x \| \boldsymbol{b}-\boldsymbol{A}\boldsymbol{x} \|\]

여기서 중요한 점은 \(\boldsymbol{A}\boldsymbol{x}\)는 항상 \(\boldsymbol{A}\)의 column space 상에 존재한다는 것이다. 이때 \(\boldsymbol{b}\)가 \(Col \boldsymbol{A}\) 상에 존재한다면 squared error의 크기가 0이 되는 \(\boldsymbol{x}\)를 찾을 수 있을 것이다.

만약 \(\boldsymbol{b}\)가 \(Col \boldsymbol{A}\) 밖에 존재한다면 \(Col \boldsymbol{A}\) 상에서 \(\boldsymbol{b}\)와 가장 가까운 지점이 squared error가 가장 작은 지점이 될 것이다. 그렇다면 이 \(\boldsymbol{A}\boldsymbol{\hat x}\)는 어떻게 찾을 수 있을까. 아래 그림을 보면 \(col \boldsymbol{A}\)에 대한 \(\boldsymbol{b}\)의 수선의 발이 Squared Error를 가장 작게 하는 \(\boldsymbol{A}\boldsymbol{\hat x}\)이라는 것을 이해할 수 있다.

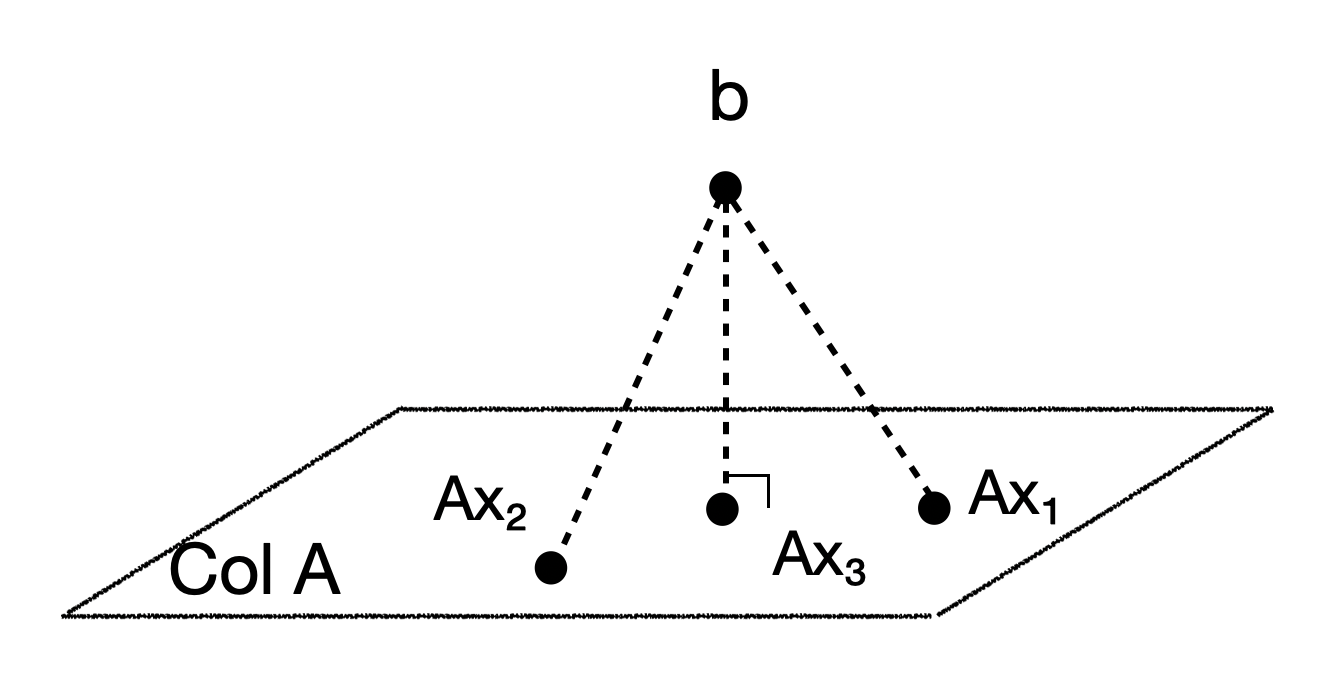
Normal Equation

그렇다면 \(col \boldsymbol{A}\) 위에서 \(\boldsymbol{b}\)의 수선의 발은 어떻게 찾을 수 있을까.

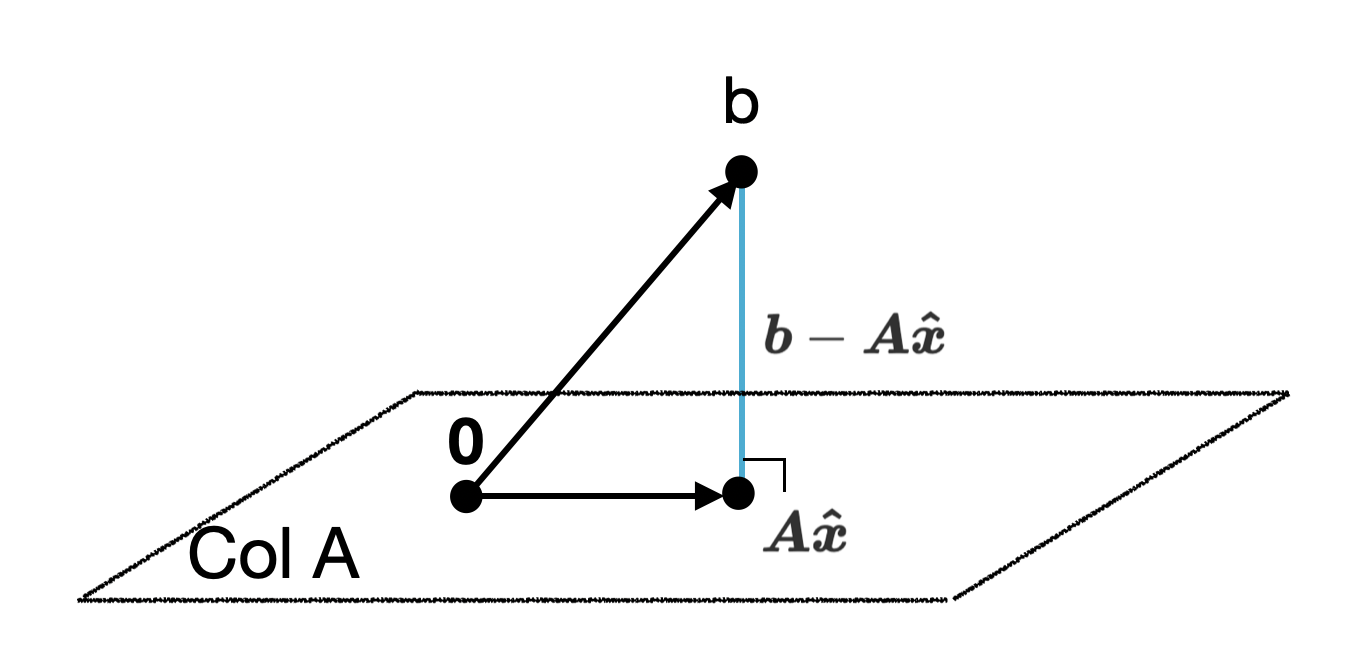
여기서 벡터 \(\boldsymbol{b} - \boldsymbol{A} \boldsymbol{\hat x}\)는 \(col \boldsymbol{A}\) 자체에 수직이므로 \(Col \boldsymbol{A}\) 상의 모든 벡터들에 대해서 수직이라고 할 수 있다. 물론 \(Col \boldsymbol{A}\)의 basis가 되는 \(\boldsymbol{A}\)의 모든 column 벡터에 대해서도 수직이다. 따라서 \(\boldsymbol{A}\)의 모든 column vector \(a\)에 대해 다음과 같이 쓸 수 있으며

\[\eqalign{ & \boldsymbol{b} - \boldsymbol{A} \boldsymbol{\hat x} \perp \boldsymbol{a_1} \\ & \boldsymbol{b} - \boldsymbol{A} \boldsymbol{\hat x} \perp \boldsymbol{a_2} \\ & ...\\ & \boldsymbol{b} - \boldsymbol{A} \boldsymbol{\hat x} \perp \boldsymbol{a_n} \\ }\]

서로 직교하는 벡터들의 내적은 0이라는 것을 이용하여 정리하면 다음과 같다.

\[\boldsymbol{A^T}(\boldsymbol{b} - \boldsymbol{A} \boldsymbol{\hat x}) = \boldsymbol{0}\]

위 식은 다음과 같이 정리할 수 있는데 이를 Normal Equation이라고 한다.

\[\boldsymbol{A^T} \boldsymbol{A} \boldsymbol{\hat x} = \boldsymbol{A^T} \boldsymbol{b}\]

즉 위의 식을 만족하는 \(\boldsymbol{\hat x}\)를 찾으면 \(\hat x = \arg \min_x \| \boldsymbol{b}-\boldsymbol{A}\boldsymbol{x} \|\)를 만족한다고 할 수 있다.

Solution 1: Invertible Matrix

역행렬을 구하는 것은 다른 문제이지만 언제나 그렇듯이 역행렬이 있다면 문제는 쉽게 풀린다. \(\boldsymbol{A^T} \boldsymbol{A}\)의 역행렬을 구할 수 있다면 \(\boldsymbol{\hat x}\)은 다음과 같이 구할 수 있다.

\[\boldsymbol{\hat x} = (\boldsymbol{A^T} \boldsymbol{A})^{-1} \boldsymbol{A^T} \boldsymbol{b}\]

Solution 2: Non-invertible Matrix

역행렬이 없다는 것은 해가 무수히 많거나, 해가 없는 경우이다. 즉 columm 벡터 간에 선형 의존인 상황을 말한다. 그런데 \(Col \boldsymbol{A}\)에 대한 \(\boldsymbol{b}\)의 수선의 발은 항상 존재하므로 역행렬이 없으면 해가 무수히 많다는 것을 의미한다.