Inner Product and Norm
- Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book과 주재걸 교수님의 강의 인공지능을 위한 선형대수를 듣고 작성했습니다.
- 또한 Transformation과 관련된 부분은 3Blue1Brown의 다음 영상을 참고하여 작성했습니다.
- update at : 2020.07.13, 2020.09.27, 2020.10.02
Inner Product
가장 기본적인 벡터 연산 중 하나인 내적(Inner Product, Dot Product)은 \(\cdot\)으로 표기하고 다음과 같이 계산된다.
\[\boldsymbol{u} = \begin{bmatrix} u_1 \\ u_2 \\ ... \\ u_n \end{bmatrix} \ \boldsymbol{v} = \begin{bmatrix} v_1 \\ v_2 \\ ... \\ v_n \end{bmatrix} \qquad \boldsymbol{u} \cdot \boldsymbol{v} = u_1v_1 + u_2v_2 + ... + u_nv_n\]내적은 다음과 같은 특성을 가진다.
\[\begin{multline} \shoveleft 1. \ \boldsymbol{u} \cdot \boldsymbol{v} = \boldsymbol{v} \cdot \boldsymbol{u}\\ \shoveleft 2. \ (\boldsymbol{u} + \boldsymbol{v}) \cdot \boldsymbol{w} = \boldsymbol{u} \cdot \boldsymbol{w} + \boldsymbol{v} \cdot \boldsymbol{w} \\ \shoveleft 3. \ (c\boldsymbol{u}) \cdot \boldsymbol{v} = c (\boldsymbol{u} \cdot \boldsymbol{v}) = \boldsymbol{u} \cdot (c\boldsymbol{v}) \\ \shoveleft 4. \ \boldsymbol{u} \cdot \boldsymbol{u} \geq 0, \ \text{and} \ \boldsymbol{u} \cdot \boldsymbol{u} = 0 \ \text{if and only if} \ \boldsymbol{u} = \boldsymbol{0} \end{multline}\]Norm
Norm이란 벡터의 크기를 측정하기 위해 사용하는 함수를 말한다. \(L_p\) norm은 다음과 같다.
\[\| x \|_p = (\Sigma_i \lvert x_i \rvert^p)^{1 \over p}, \qquad \text{for} \ p \in \rm l\!R, \ p \geqq 1\]크기를 측정하는 함수로서 \(L_p\) norm은 벡터를 입력으로 받아 음수가 아닌 실수의 값을 반환한다. 직관적으로는 origin부터 벡터 \(x\)가 가리키는 지점 사이의 거리를 의미하며, 다음과 같은 특성을 만족하는 함수이다.
\[\begin{multline} \shoveleft 1. \ f(x) = 0 \rightarrow x = 0 \\ \shoveleft 2. \ f(x+y) \geqq f(x) + f(y) \\ \shoveleft 3. \ \text{for all} \ \alpha \in \rm l\!R, \ f(\alpha x) = \lvert \alpha \rvert f(x) \end{multline}\]Types of Norms
위의 식에서 \(p\)를 무엇으로 하는가에 따라 다양한 종류의 Norm이 있다.
\(L^2\) Norm
가장 많이 사용되는 \(L_p\) norm은 \(p=2\)인 \(L^2\) norm이다. \(L^2\) norm은 origin에서 벡터 \(\boldsymbol{x}\)까지의 거리가 유클리디안 거리로 측정한 것과 동일하기 때문에 Euclidean norm으로도 불린다. 머신러닝에서 자주 사용되기 때문에 \(\| x \|\)와 같이 2를 생략하고 표기하기도 한다.
\[\| \boldsymbol{x} \|_2 = \root 2 \of {x_1^2 + x_2^2 + ... + x_n^2} = \root 2 \of {\boldsymbol{v} \cdot \boldsymbol{v}} \\\]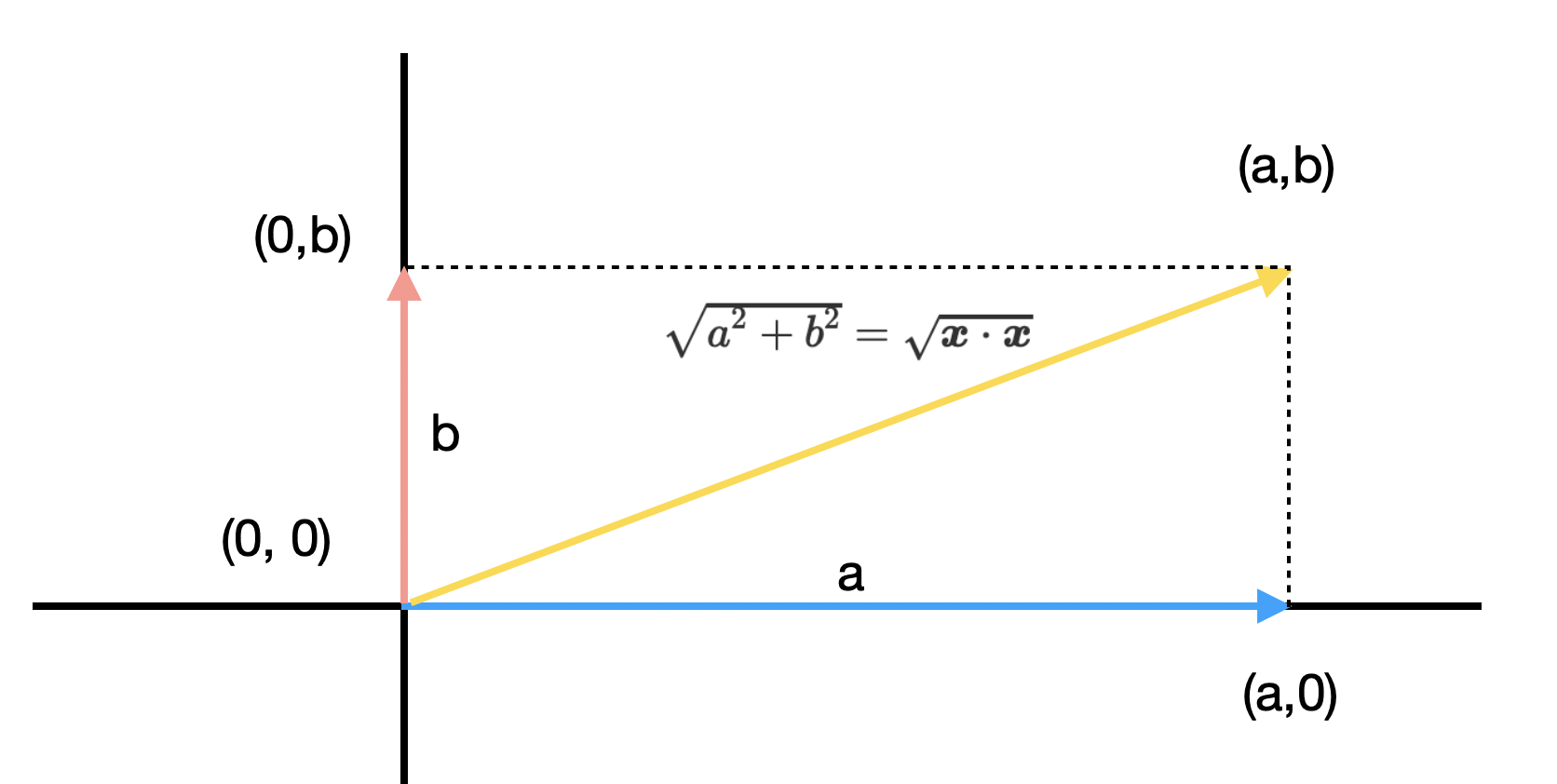
\(L^2\) norm과 함께 squared \(L^2\) norm도 많이 사용된다. squared \(L^2\) norm은 \(x^T x\), 즉 벡터의 내적으로 비교적 단순하게 계산할 수 있으므로 편리하다. 또한 squared \(L^2\) norm의 미분값은 전체 벡터에 영향을 받는 \(L^2\) norm과는 달리 관련있는 요소에 대해서만 영향을 받는다는 점에서도 이점이 있다.
\[\| \boldsymbol{x} \|_2^2 = \boldsymbol{v} \cdot \boldsymbol{v}\]\(L^1\) Norm
하지만 squared \(L^2\) Norm은 Origin 부근에서는 매우 천천히 증가한다는 단점이 있다. 몇몇 머신러닝 방법론 중에는 0일 때와 그렇지 않을 때를 엄밀하게 구분할 것을 요구하기도 하는데 이러한 경우에는 Squared \(L^2\) norm이 적절하지 않다고 할 수 있다. \(L^1\) Norm은 계산의 편의성을 유지하면서도 이러한 문제를 해소할 수 있는 대안으로 사용된다.
\[\| x \|_1 = \Sigma_i \lvert x_i \rvert\]\(L^{\infty}\) Norm
\(L^{\infty}\) norm은 Max Norm이라고도 불리는데, 다음과 같이 전체 Element 중 크기가 가장 큰 것으로 계산된다.
\[\| x \|_{\infty} = max_i \lvert x_i \rvert\]Unit Vector
단위 벡터(Unit Vector)란 벡터의 Norm이 1인 벡터를 의미한다. 다양한 크기와 방향을 가진 벡터들을 방향은 남기고 길이는 모두 1로 normalize해야하는 경우가 있는데 다음 공식에 따라 단위 벡터로 만들어 준다.
\[\boldsymbol{u} = {1 \over \| \boldsymbol{v} \|} \boldsymbol{v}\]Distance between vectors
두 벡터가 얼마나 떨어져 있는가 또한 Norm으로 정의할 수 있다. 구체적으로 두 벡터 간의 거리는 다음과 같이 정의된다.
\[\text{dist}(\boldsymbol{u}, \boldsymbol{v}) = \| \boldsymbol{u} - \boldsymbol{v} \|\]그림으로 보면 조금 더 직관적으로 이해가 된다.
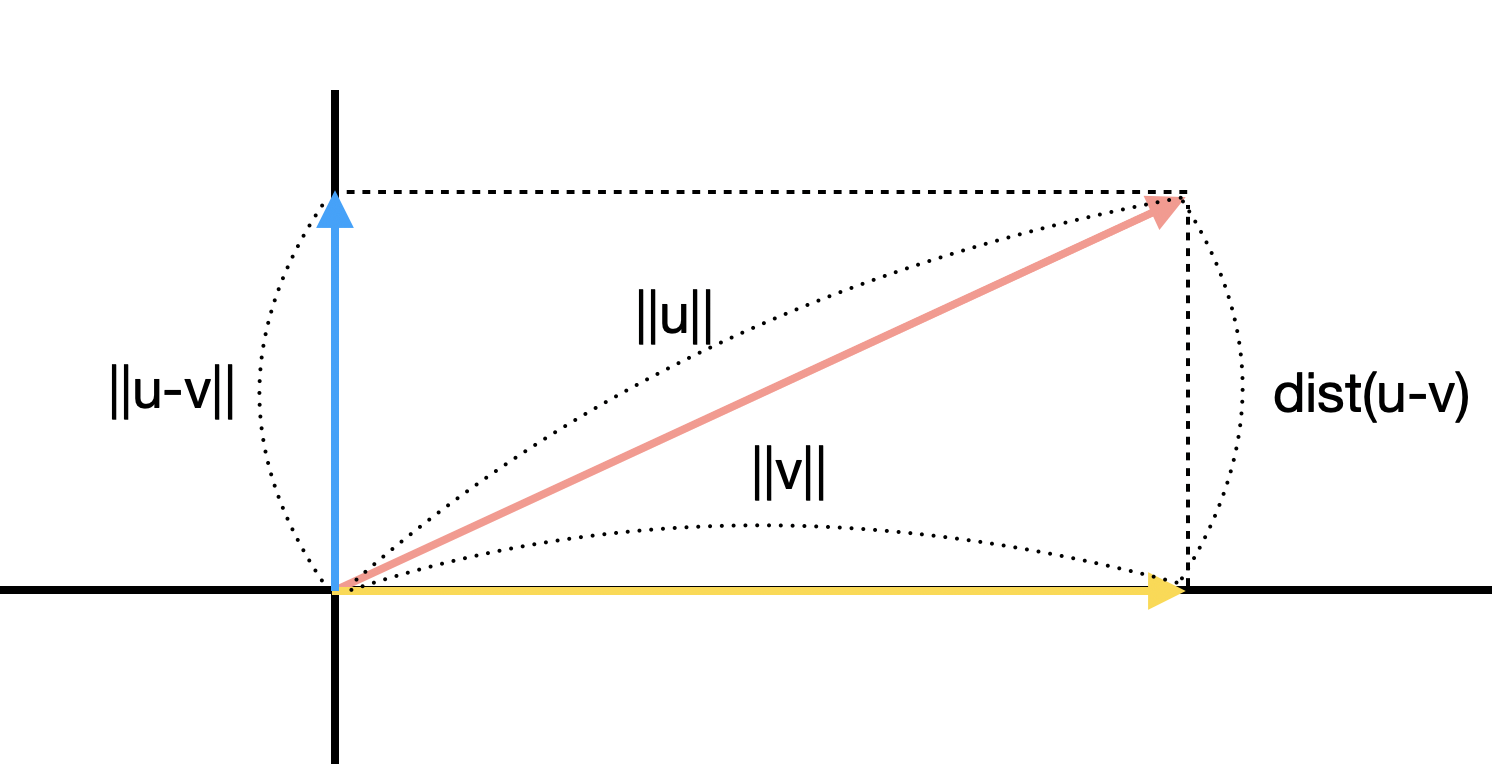
\(L^2\) norm과 Inner Product
어떤 두 벡터 간의 Inner Product는 다음과 같이 \(L^2\) Norm과 벡터 간 각도의 \(\cos \theta\)를 곱하여 표현할 수 있다.
\[\boldsymbol{a}^T \boldsymbol{b} = \| \boldsymbol{a} \|_2 \| \boldsymbol{b} \|_2 \cos \theta, \qquad \theta \ \text{is the angle between } \boldsymbol{a} \text{ and } \boldsymbol{b}\]이는 다음과 같이 증명이 가능하다.
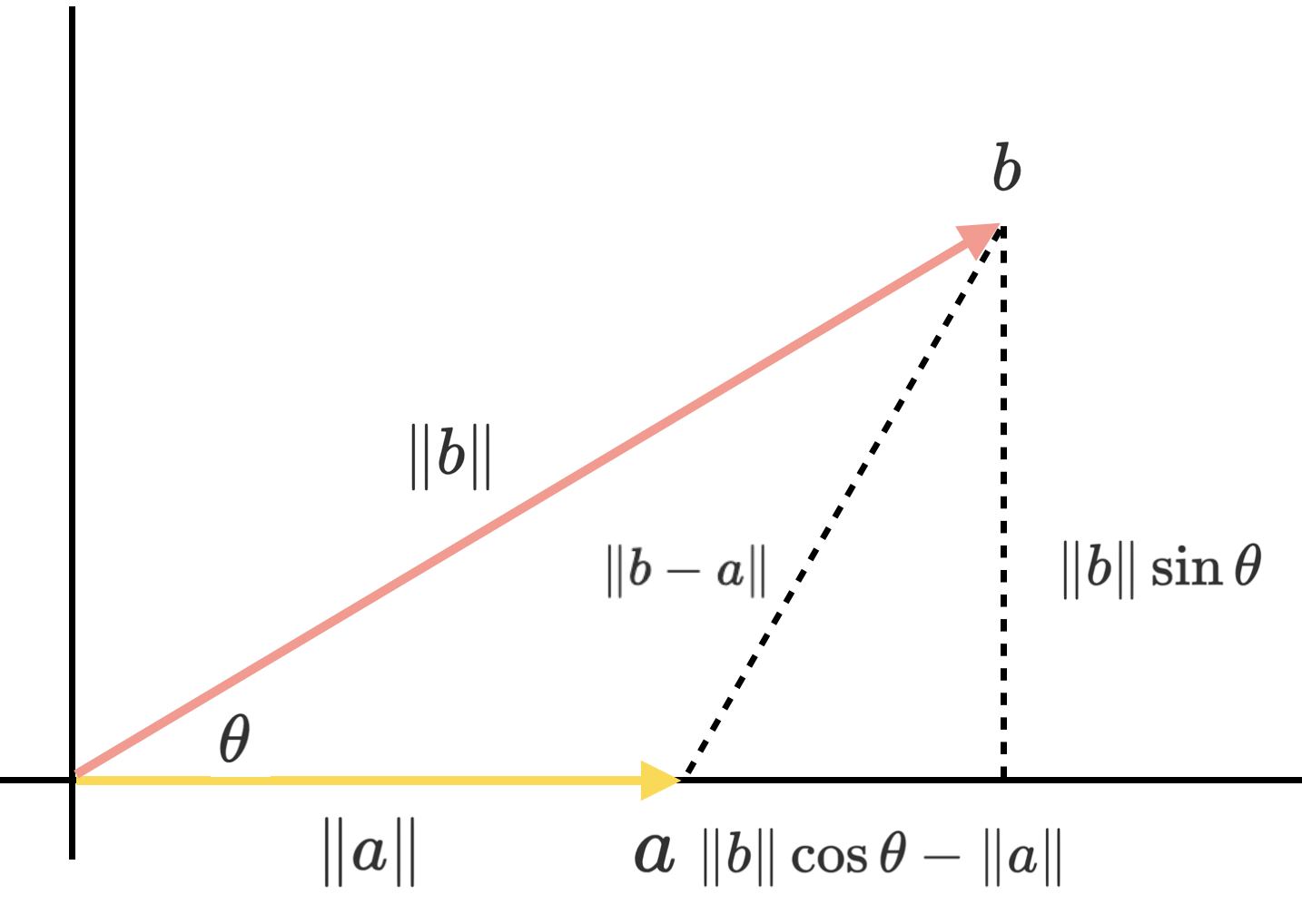
이때 \(\cos\) 함수는 아래와 같이 0도에서 1, 직각에서(90도, 270도)에서 0의 값을 가진다.
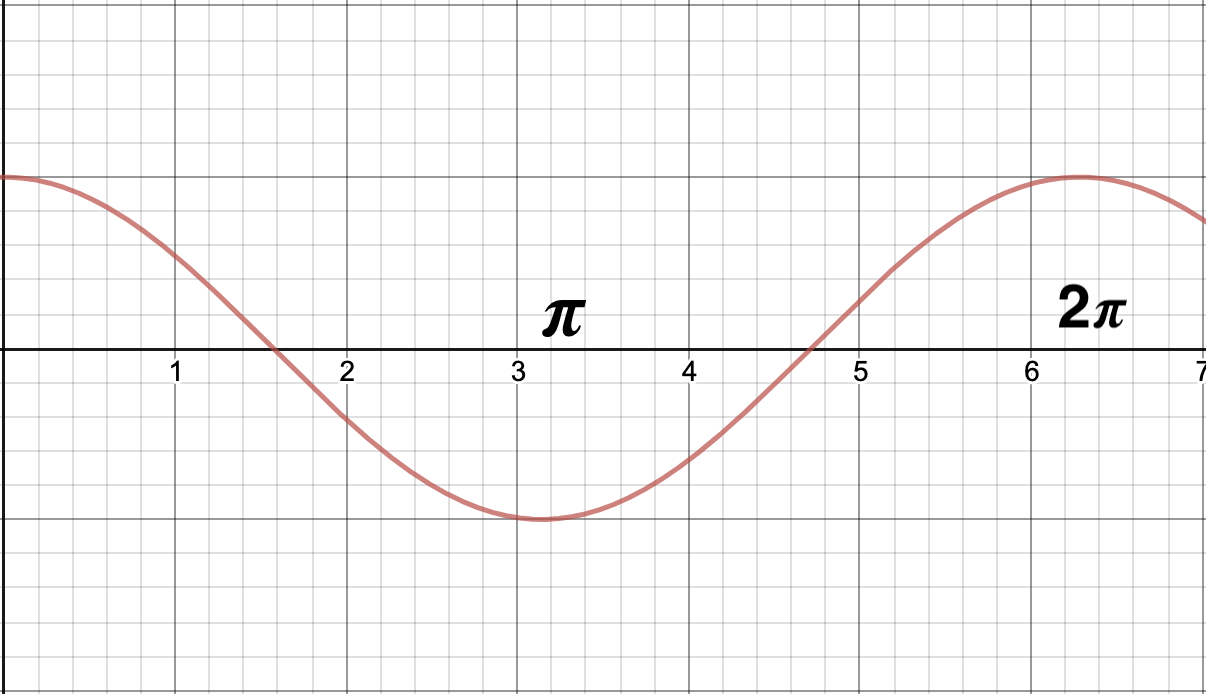
이를 통해 두 가지를 추론할 수 있다.
- 두 벡터의 크기가 일정하다면 방향이 동일할 때 내적의 크기가 가장 커진다.
- 두 벡터의 내적이 0이고, 두 벡터가 모두 영백터가 아니라면 두 벡터는 직교(orthogonal)한다.
Cauchy-Schwarz Inequality
위에서 확인한 식
\[\boldsymbol{a} \cdot \boldsymbol{b} = \| \boldsymbol{a} \|_2 \| \boldsymbol{b} \|_2 \cos \theta\]를 통해 다음과 같은 부등식을 유도할 수 있다.
\[\| \boldsymbol{a} \|^2 \| \boldsymbol{b} \|^2 \geq \lvert \boldsymbol{a} \cdot \boldsymbol{b} \rvert^2\]이를 코시 슈바르츠 부등식(Cauchy-Schwarz Inequality)이라고 한다. 이는 다음과 같이 증명이 가능하다.
\[\eqalign{ &\eqalign{ \| \boldsymbol{a} \|^2 \| \boldsymbol{b} \|^2 &\geq \lvert \| \boldsymbol{a} \| \| \boldsymbol{b} \| \cos \theta \rvert^2\\ &= \| \boldsymbol{a} \|^2 \| \boldsymbol{b} \|^2 \cos^2 \theta\\ }\\ & \Rightarrow 1 \geq \cos^2 \theta \qquad \qquad (\because \| \boldsymbol{a} \|^2, \| \boldsymbol{b} \|^2 > 0) \\ & \Rightarrow 1 \geq \lvert \cos \theta \rvert }\]\(\cos\) 함수는 항상 1보다 작거나 같으므로 성립한다는 것을 알 수 있다. 이때 등호는 \(\cos \theta = 1\)일 때, 즉 \(\theta\)가 0 또는 \(\pi\)인 경우에만 가능하다.
Inner Product & Linear Transformation
또한 아래 식을 통해 벡터의 내적과 선형 변환의 관계 또한 생각해 볼 수 있다.
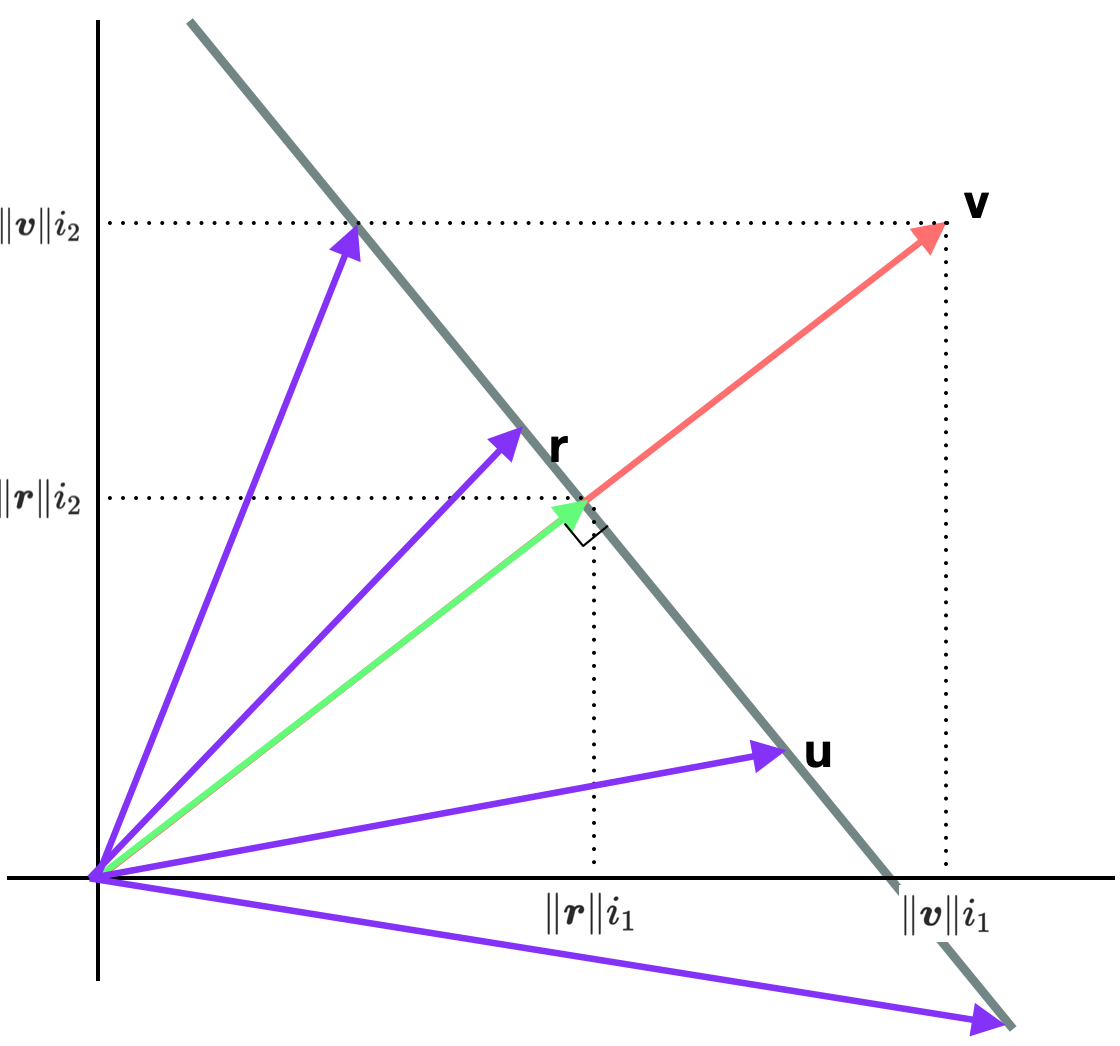
\[\boldsymbol{u} \cdot \boldsymbol{v} = \| \boldsymbol{u} \|_2 \| \boldsymbol{v} \|_2 \cos \theta, \qquad \theta \ \text{is the angle between } \boldsymbol{u} \text{ and } \boldsymbol{v}\]우선 위의 식을 그림으로 표현하면 다음과 같다.
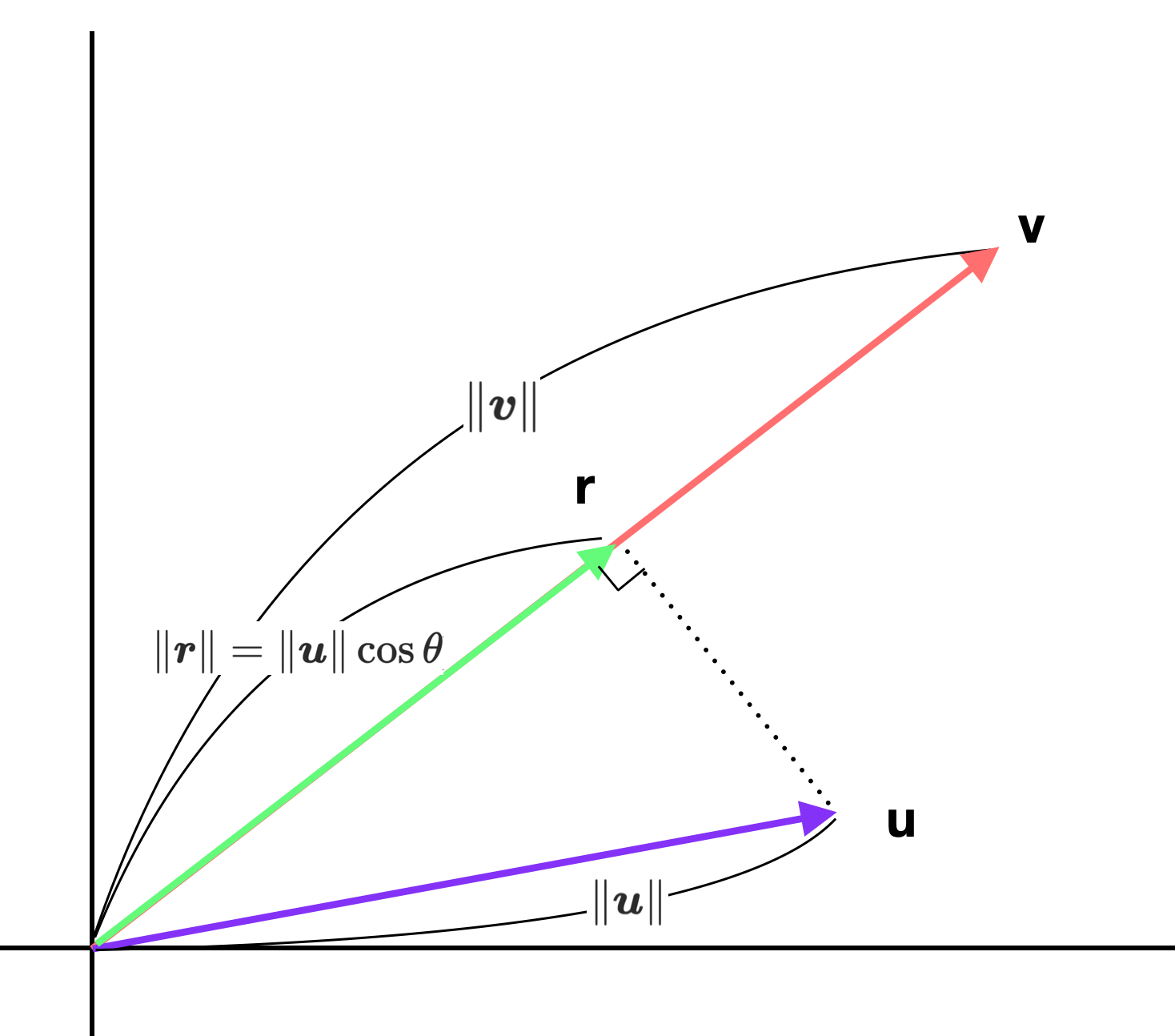
위의 그림에서 벡터 \(\boldsymbol{r}\)은 \(\boldsymbol{u}\)에서 \(\boldsymbol{v}\)로 수선을 내렸을 때 얻어지는 벡터이다. 다르게 말하면 \(\boldsymbol{u}\)를 \(\text{span } \boldsymbol{v}\)상으로 선형변환을 통해 얻은 벡터라고 할 수 있다. 이때 \(\boldsymbol{u}\)와 \(\boldsymbol{r}\)은 직각삼각형을 이루므로 \(\| \boldsymbol{r} \| = \| \boldsymbol{u} \| \cos \theta\)가 성립한다 결과적으로 다음과 같이 적을 수 있다.
\[\boldsymbol{u} \cdot \boldsymbol{v} = \| \boldsymbol{r} \| \| \boldsymbol{v} \|\]즉 \(\boldsymbol{u} \cdot \boldsymbol{v}\)는 \(\boldsymbol{u}\)에서 \(\boldsymbol{v}\)로 수선을 내려 구한 벡터 \(\boldsymbol{r}\)과 비교할 때 \(\boldsymbol{v}\)가 얼마나 더 큰지를 의미한다고 할 수 있다.
그런데 위와 같은 두 벡터 \(\boldsymbol{u}, \boldsymbol{v}\) 간의 내적 연산은 다음과 같은 선형 변환(Linear Transformation)식과 매우 유사하다. 즉 \(\boldsymbol{u} \cdot \boldsymbol{v}\)은 \(\boldsymbol{u}\)를 \(\text{span } \boldsymbol{v}\)에 매핑한 것과 어떤 관계가 있음을 생각해 볼 수 있다.
\[\eqalign{ & \text{[Inner Product]}\\ & \qquad \begin{bmatrix} u_1 \\ u_2 \\ ... \\ u_n \end{bmatrix} \ \cdot \begin{bmatrix} v_1 \\ v_2 \\ ... \\ v_n \end{bmatrix} = u_1v_1 + u_2v_2 + ... + u_nv_n\\ \\ \\ & \text{[Linear Transformation]}\\ & \qquad \begin{bmatrix} &v_1, &v_2, &..., &v_n \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \\ ... \\ u_n \end{bmatrix} = u_1v_1 + u_2v_2 + ... + u_nv_n }\]그렇다면 \(\boldsymbol{u}\)를 \(\text{span } \boldsymbol{v}\) 상에 매핑하면 어떻게 될까. 이는 \(\boldsymbol{u}\)를 \(\text{span } \boldsymbol{v}\)의 Unit Vector \(\hat i\)로 선형 변환하면 쉽게 구할 수 있으며, 그 결과는 \(\| \boldsymbol{r} \|\)이 된다.
\[\| \boldsymbol{r} \| = \begin{bmatrix} &i_1, &i_2 \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} = u_1i_1 + u_2i_2\]위 식은 \(\boldsymbol{v}\)에 맞춰 다음과 같이 표현할 수 있다. 그리고 이는 곧 \(\boldsymbol{u} \cdot \boldsymbol{v}\)가 된다.
\[\boldsymbol{u} \cdot \boldsymbol{v} = \| \boldsymbol{r} \| \| \boldsymbol{v} \| = \begin{bmatrix} & \| \boldsymbol{v} \| i_1, & \| \boldsymbol{v} \| i_2 \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} = \| \boldsymbol{v} \| u_1i_1 + \| \boldsymbol{v} \| u_2i_2\]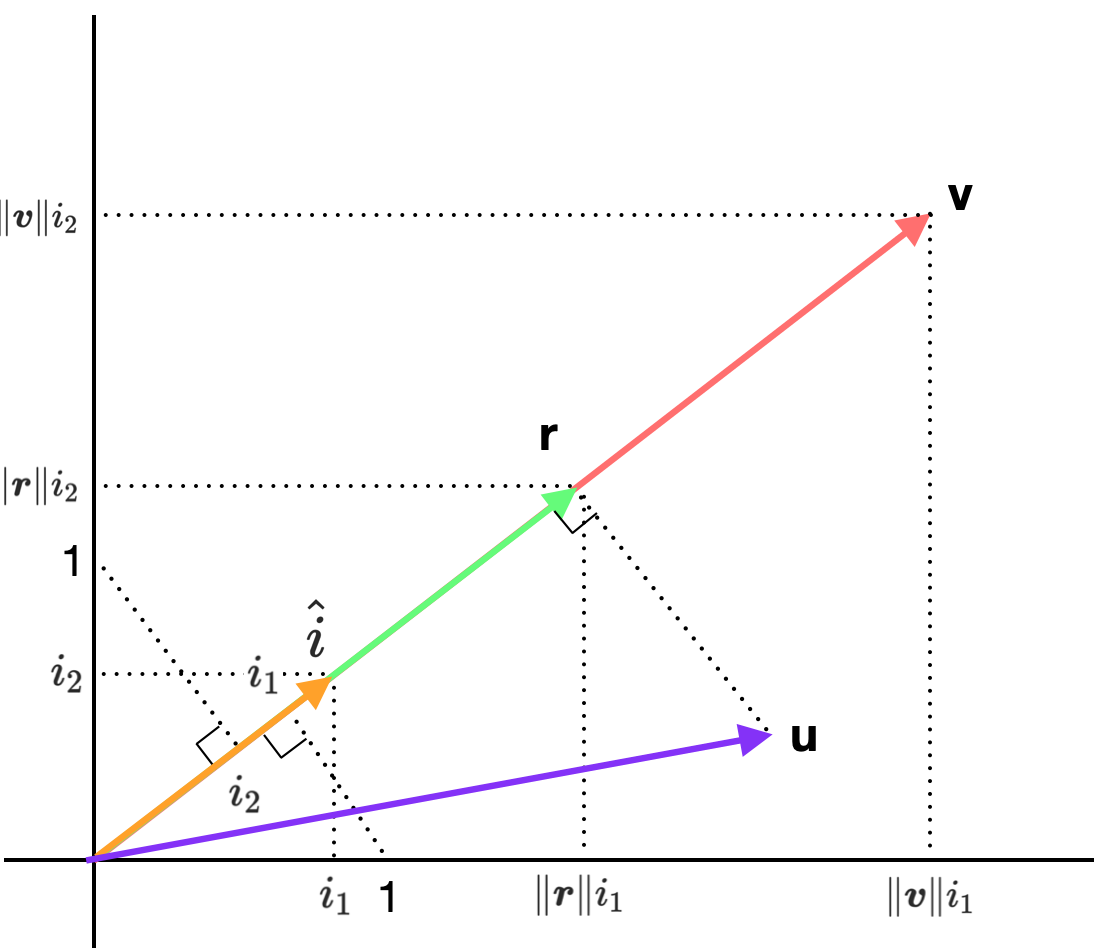
이를 통해 한 가지 유추할 수 있는 것은 \(\hat i\)로의 선형 변환 결과가 \(\boldsymbol{r}\)인 모든 벡터는 \(\boldsymbol{v}\)와의 내적 값이 동일하다는 것이다. 즉 아래 그림에서 회색 선 위의 모든 벡터들은 \(\boldsymbol{v}\)와의 내적 값이 모두 같다.