Linear Mapping

• Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book과 주재걸 교수님의 강의 인공지능을 위한 선형대수를 듣고 작성했습니다.
• 김홍종 교수님의 미적분학 1을 참고하여 수정했습니다.
• Update at : 2020.07.12 2021.01.03

Subspace & Basis

Subspace과 Basis는 다음과 같이 정의된다.

• A subspace H is defined as a subset of \(R^n\) closed under linear combination
• A basis of a subspace H is a set of vectors that satisfies both of the following
  • Fully spnas the given subspace H
  • Linear Independent

subspace란 어떤 vector 집합에 포함되어 있는 모든 vector 간 선형 결합에 대해 닫혀있는 벡터 집합을 말한다. 여기서 선형 결합에 닫혀있다는 것은 집합 내의 어떤 vector 간에 선형 결합을 하더라도 집합 내에 포함되어 있는 vector가 구해진다는 것을 의미한다. 그리고 기저(Basis)는 이러한 subspace를 선형 결합을 통해 완전히 커버할 수 있는(span) 선형 독립 벡터들의 집합이 된다.

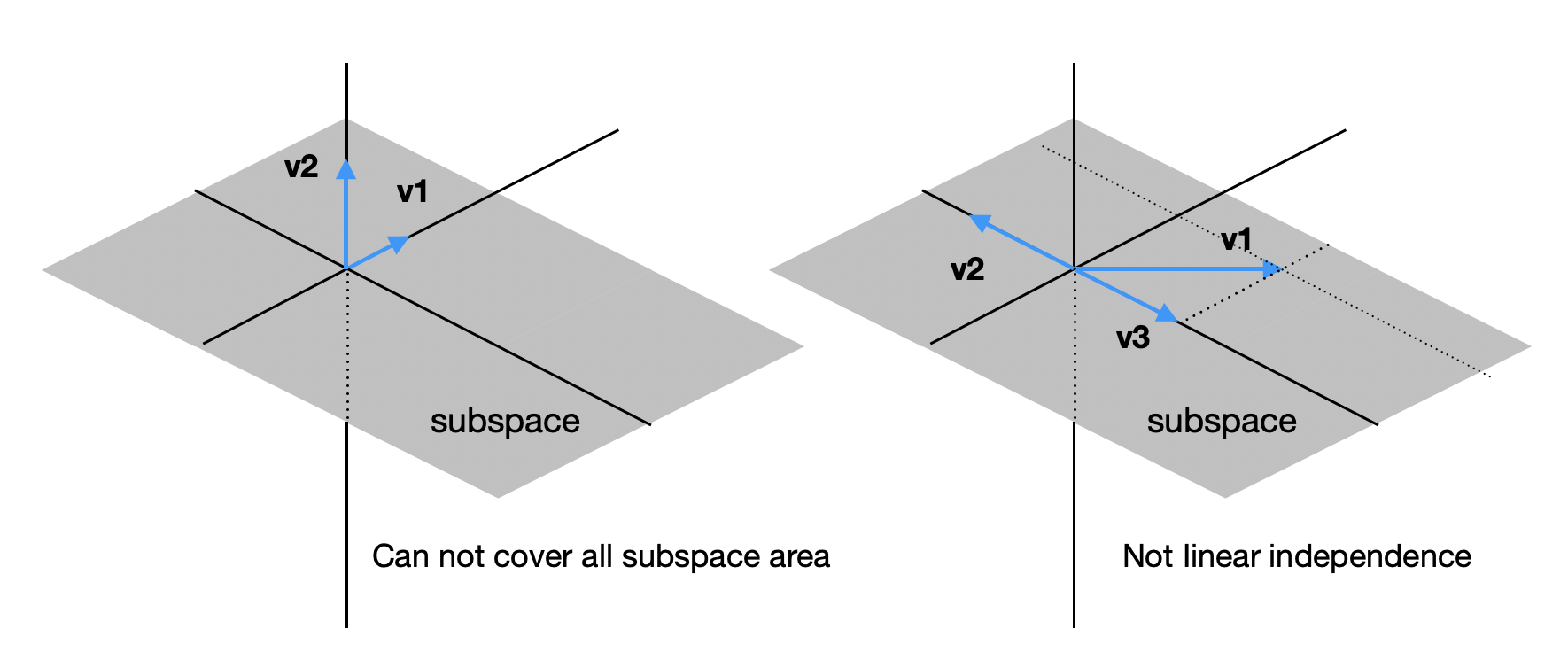
아래 두 예시의 경우 모두 기저의 조건을 만족하지 못한다. 구체적으로 왼쪽 예시는 두 vector가 subspace를 모두 커버하지 못하기 때문이고 오른쪽 예시에서는 세 개의 vector가 선형 의존의 관계를 가지기 때문이다.

기저는 subpace에 대해 유일하지 않고, 아래와 같이 기저의 조건만 만족한다면 여러 조합이 존재할 수 있다.

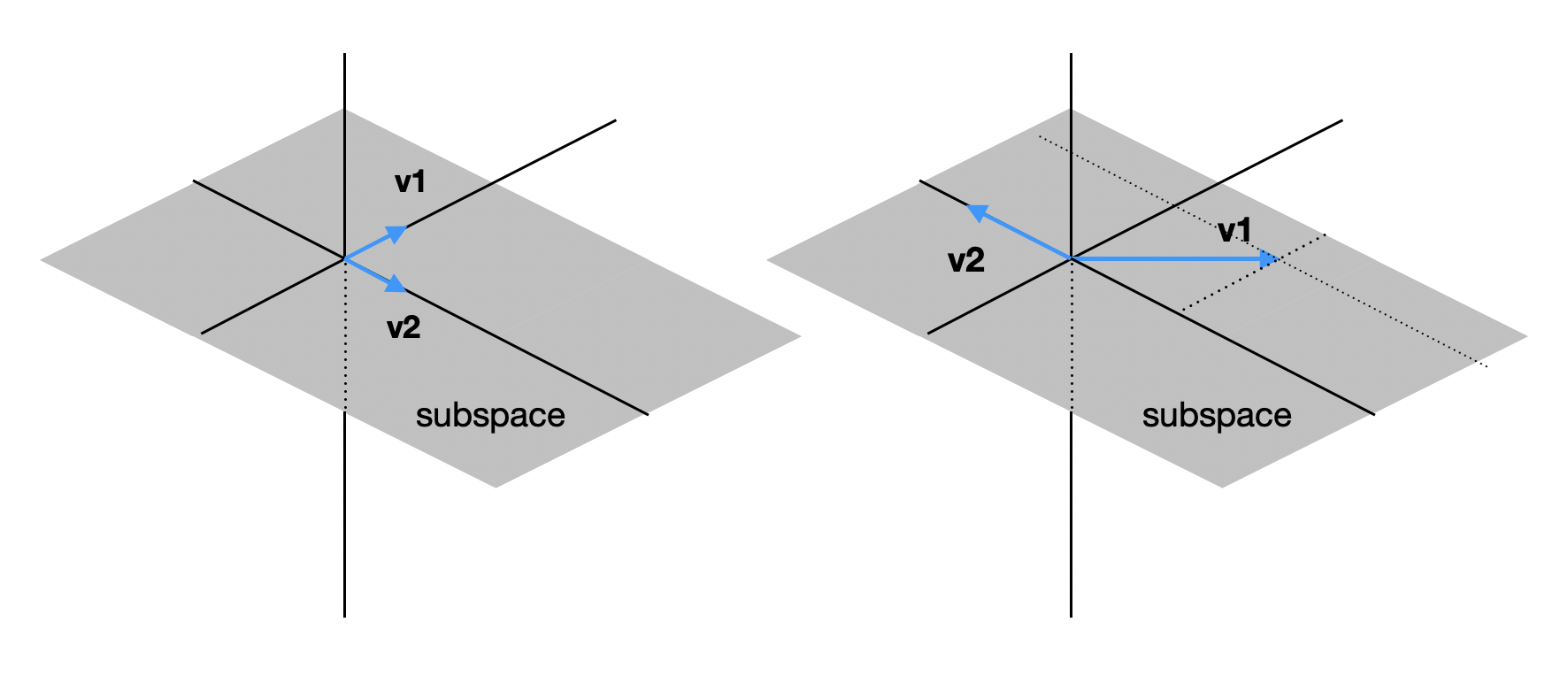
참고로 Subspace의 차원은 기저 벡터의 갯수로 정의된다.

Standard Basis

n 차원의 subspace를 표현하기 위해 사용되는 표준 기저는 다음과 같이 어느 한 성분만 1이고 나머지는 모두 0인 기저 벡터들의 집합를 말한다. 3차원의 경우 다음과 같다.

\[\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \ \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \ \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\]

표준 기저를 모두 concat하여 표현하면 Identity Matrix와 동일해진다.

Linear Mapping

선형 결합(Linear Combination)은 주어진 벡터 간에 벡터 연산을 통해 새로운 벡터를 만들어내는 것이므로 Subspace는 변화하지 않는다. 반면 선형 사상(Linear Mapping)은 이름 그대로 어떤 한 벡터를 다른 벡터로 매핑하는 것을 의미하며, 이 과정에서 Subspace가 새롭게 정의될 수도 있다. 즉 2차원 평면 상의 벡터가 선형 변환을 통해 3차원 공간 상의 벡터로 변화할 수 있다는 것이다. 물론 선형 변환인 만큼 이 과정에서도 선형성의 조건을 만족해야 한다(위키피디아).

• 벡터 공간 \(V, W\)
• 선형 변환 \(T : V \rightarrow W\)
• 임의의 두 벡터 \(u, v \in V\)에 대하여 \(T(u+v) = T(u) + T(v)\)
• 임의의 스칼라 \(a \in K\) 및 벡터 \(v \in V\)에 대하여 \(T(av) = a T(v)\)

Matrix Multiplication and Linear Mapping

선형 사상을 쉽게 하는 방법은 기저 벡터들의 선형 변환을 Matrix 형태로 만들어 변환하고자 하는 vector에 곱해주는 것이다. 예를 들어 2차원의 벡터 공간 \(V\) 상의 vector \(v\)를 3차원의 벡터 공간 \(W\)의 벡터로 변환한다고 해 보자. 이때 \(V\)의 기저벡터가 다음과 같이 주어져 있고

\[\begin{bmatrix} 1 \\ 0 \\ \end{bmatrix}, \ \begin{bmatrix} 0 \\ 1 \\ \end{bmatrix}\]

그 선형 사상의 결과가 다음과 같다면

\[T(\begin{bmatrix} 1 \\ 0 \\ \end{bmatrix}) = \begin{bmatrix} 3 \\ 1 \\ 2 \end{bmatrix}, \qquad T(\begin{bmatrix} 0 \\ 1 \\ \end{bmatrix}) = \begin{bmatrix} 4 \\ -2 \\ 7 \end{bmatrix}\]

vector \(v = \begin{bmatrix} 3 \\ 2 \\ \end{bmatrix}\)는 벡터 공간 \(W\)에 다음과 같이 \(\begin{bmatrix} 17 \\ -1 \\ 20 \end{bmatrix}\)로 매핑된다.

\[\begin{bmatrix} 3 && 4 \\ 1 && -2 \\ 2 && 7 \end{bmatrix} \begin{bmatrix} 3 \\ 2 \\ \end{bmatrix} = \begin{bmatrix} 17 \\ -1 \\ 20 \end{bmatrix}\]

이러한 점에서 행렬은 어떤 공간의 벡터들을 다른 공간의 벡터로 매핑하는 선형 사상이라고 할 수 있다. 반대로 모든 선형 사상은 행렬에서 얻어진다는 것 또한 증명이 되어 있다. 따라서 행렬과 선형 사상은 동일한 것이다(미적분학1, 235).

Meaning of Matrix Multiplication

이와 같이 본다면 어떤 벡터 \(\boldsymbol{x}\)에 행렬 \(\boldsymbol{A}\)를 곱해준다는 것은 벡터 \(\boldsymbol{x}\)를 행렬 \(\boldsymbol{A}\) 열벡터들이 기저가 되는 공간 \(\text{Col}\boldsymbol{A}\)에 매핑하는 것이 된다.

\[\boldsymbol{b} = \boldsymbol{C_1}\boldsymbol{x_1} + \boldsymbol{C_2}\boldsymbol{x_2} + \boldsymbol{C_3}\boldsymbol{x_3} + \boldsymbol{C_4}\boldsymbol{x_4}\]

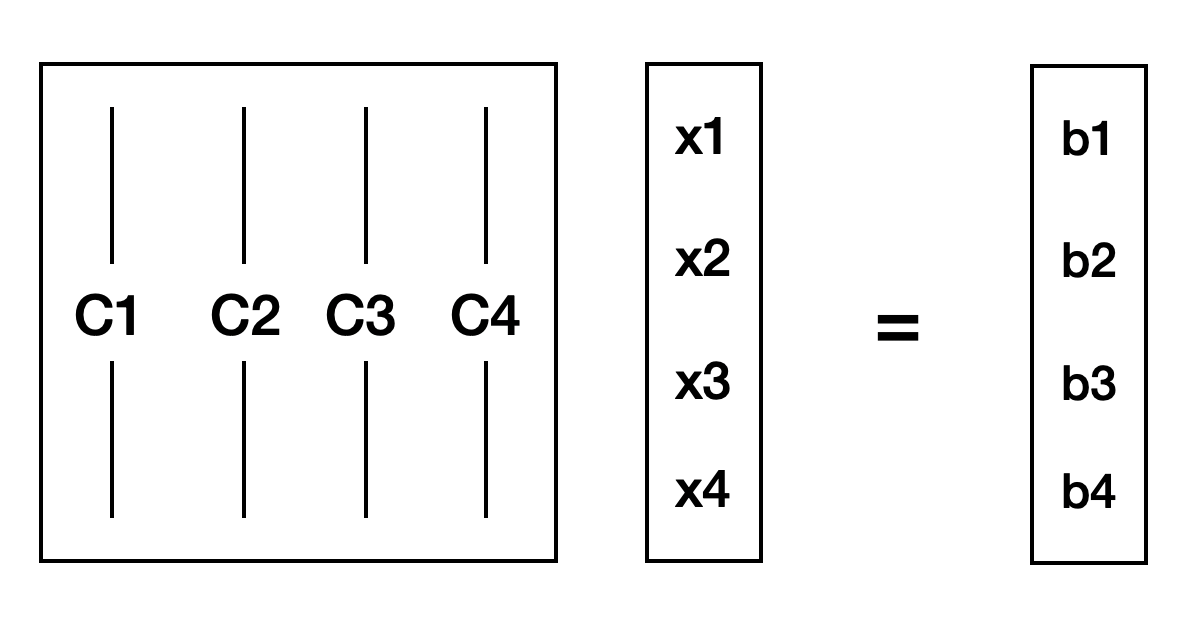
위 식을 통해 벡터에 행렬을 곱한 결과는 행렬의 열백터 간의 선형 결합이라는 것을 알 수 있다.

Linear Mapping and Nueral Network

뉴럴넷은 기본적으로 벡터와 행렬의 곱셈으로 표현된다. 물론 activation function 등에 의해 연산 과정에서 선형성은 보존할 수 없지만 weight를 곱하는 것은 결국 Matrix와 Vector를 곱해 새로운 Vector로 변환하는 것이므로 뉴럴넷에서 하나의 레이어를 통과하는 것은 선형 변환이라고 할 수 있다.

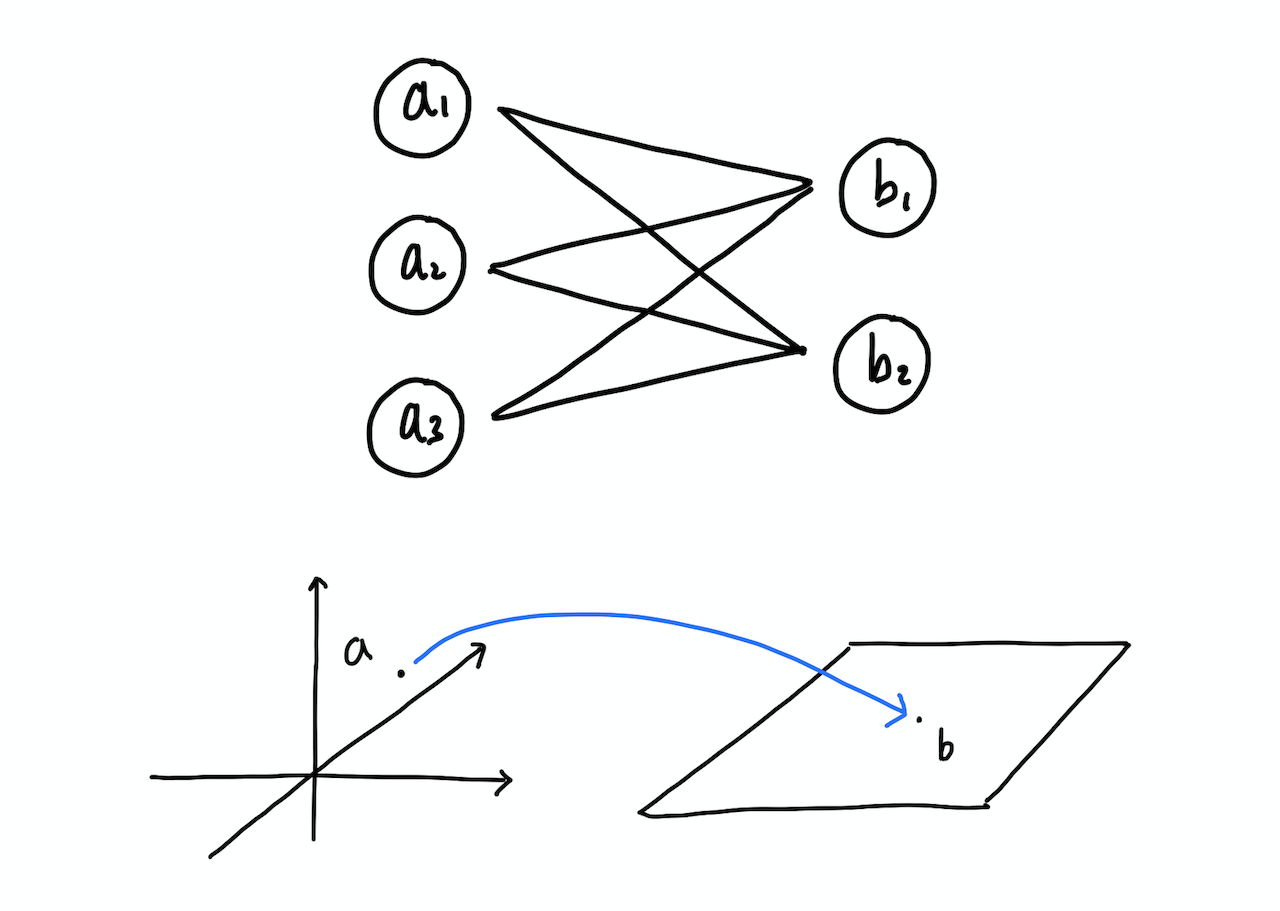
Example: AutoEncoder

AutoEncoder는 기본적인 뉴럴넷 구조 중 하나로 차원 축소를 진행하는 Encoder와 이를 다시 원래의 차원으로 복원하는 Decoder로 구성된다. Encoder의 출력값이자 Decoder의 입력값을 일반적으로 latent라고 부르는데 latent의 차원 수는 원데이터의 차원 수보다 작기 때문에 Decoder의 역할은 원데이터의 차원 속에서 이를 잘 표현할 수 있는 작은 차원의 공간을 찾는 것이 된다.

예를 들어 원데이터가 3차원이고 latent가 2차원이라면 Decoder는 3차원 공간 속에서 데이터를 가장 잘 모사하는 2차원 평면을 찾도록 학습한다. 하지만 아무리 잘 학습한다 하여도 3차원 전체 공간을 2차원 평면으로 표현하는 데에는 한계가 있을 수 밖에 없는데 잘 학습된 Decoder라면 불필요한 요소는 버리고 중요한 특징을 커버하는 평면을 선택하게 될 것이다.

경우에 따라서는 3차원 공간 속에서 2차원 평면으로는 표현할 수 없는 형태로 특징들이 분포하고 있을 수도 있다. 이때 평면을 구부릴 수 있다면 보다 표현력이 좋아질 것이라 기대할 수 있는데 이것이 가능하도록 해 주는 것이 딥러닝에서 필수적으로 사용되는 sigmoid, relu와 같은 non-linear activation function들이다. 즉 선형 사상으로는 선형 공간만 모사할 수 있었던 반면 non-linear function을 더하여 구불구불한 공간까지도 표현할 수 있게 된 것이다. 이때 구불구불한 공간을 Manifold라고 한다.