Linear Combination

• Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book과 주재걸 교수님의 강의 인공지능을 위한 선형대수를 듣고 작성했습니다.
• update at : 2020.07.11

Linear Combination

아래와 같은 \(\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}\) 가 있다고 하자.

\[\begin{bmatrix} a_{11} && a_{12} && a_{13} \\ a_{21} && a_{22} && a_{23} \\ a_{31} && a_{32} && a_{33} \\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} b_1\\ b_2\\ b_3 \end{bmatrix}\]

위의 식은 Matrix의 column별로 분해하여 다음과 같이 쓸 수 있다.

\[x_1 \begin{bmatrix} a_{11} \\ a_{21} \\ a_{31} \\ \end{bmatrix} + x_2 \begin{bmatrix} a_{12} \\ a_{22} \\ a_{32} \\ \end{bmatrix} + x_3 \begin{bmatrix} a_{13} \\ a_{23} \\ a_{33} \\ \end{bmatrix} = \begin{bmatrix} b_1\\ b_2\\ b_3 \end{bmatrix}\]

위키피디아에서는 선형 결합(Linear Combination)을 백터들의 스칼라배와 백터 덧셈을 통해 새로운 벡터를 얻는 연산이라고 정의하는데, 이렇게 본다면 Matrix와 Vector 간의 곱은 Vector 간의 선형 결합이라고 할 수 있다.

Column Space

행렬을 구성하는 vector를 column vector라고 한다. 예를 들어 행렬 \(\boldsymbol{A}\)가 다음과 같이 정의된다고 할 때

\[\boldsymbol{A} = \begin{bmatrix} a_{11} && a_{12} && a_{13} \\ a_{21} && a_{22} && a_{23} \\ a_{31} && a_{32} && a_{33} \\ \end{bmatrix}\]

column vector는

\[\begin{bmatrix} a_{11} \\ a_{21} \\ a_{31} \\ \end{bmatrix} \ \begin{bmatrix} a_{12} \\ a_{22} \\ a_{32} \\ \end{bmatrix} \ \begin{bmatrix} a_{13} \\ a_{23} \\ a_{33} \\ \end{bmatrix}\]

이라고 할 수 있다. 이러한 column vector로 표현할 수 있는 공간을 column space라고 한다.

Span

Span이란 영백터가 아닌 벡터들의 집합을 선형 결합하여 나타낼 수 있는 vector들의 집합으로 정의된다. 예를 들어 벡터 \(\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\)의 span은 다음과 같이 직선이다.

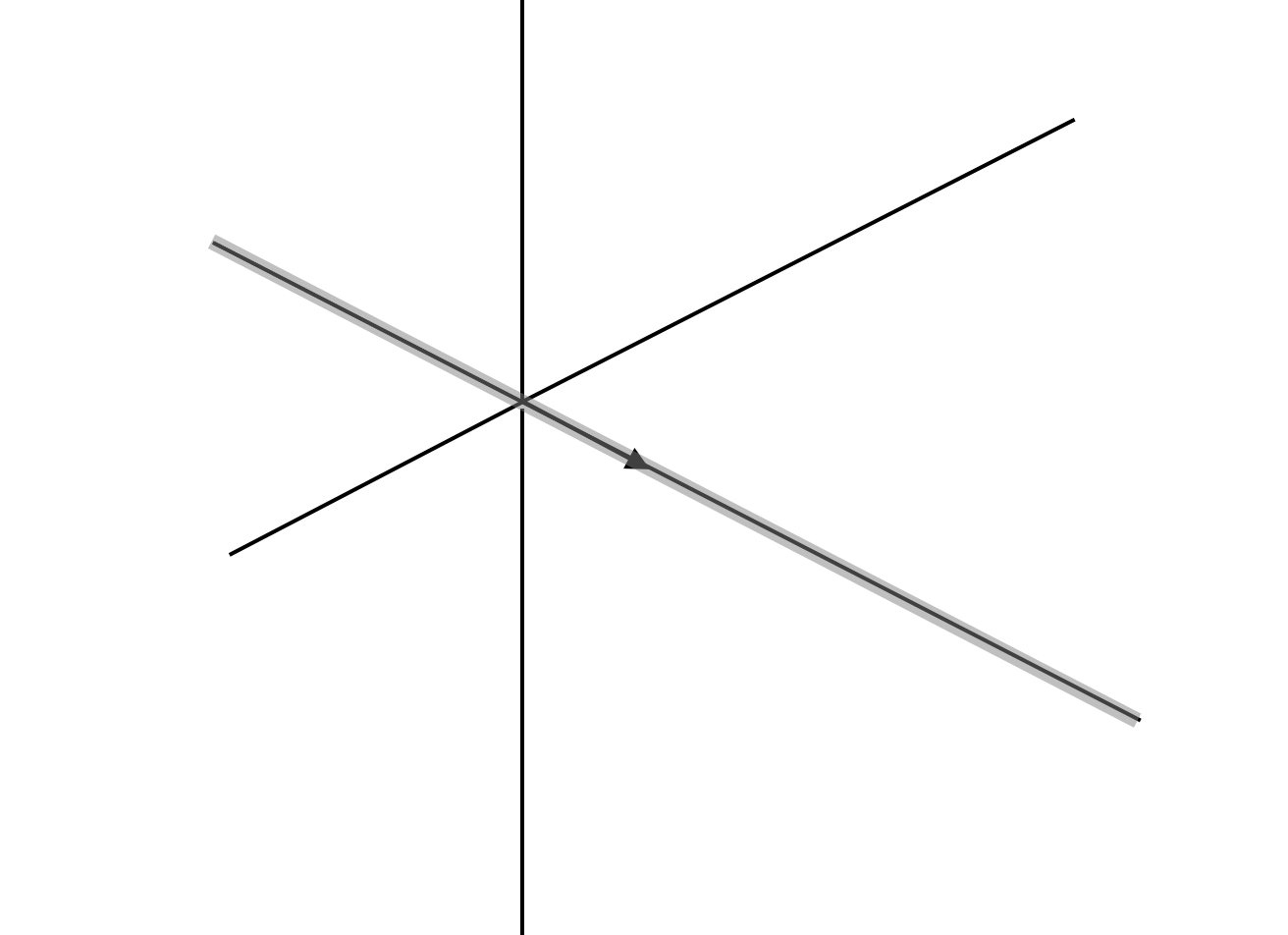
Span의 크기는 벡터의 갯수가 늘어나면 늘어날수록 커질 수 있다. 예를 들어 1번 예시의 벡터 \(\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\)와 \(\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\)의 span을 구한다면 다음과 같이 평면이 된다.

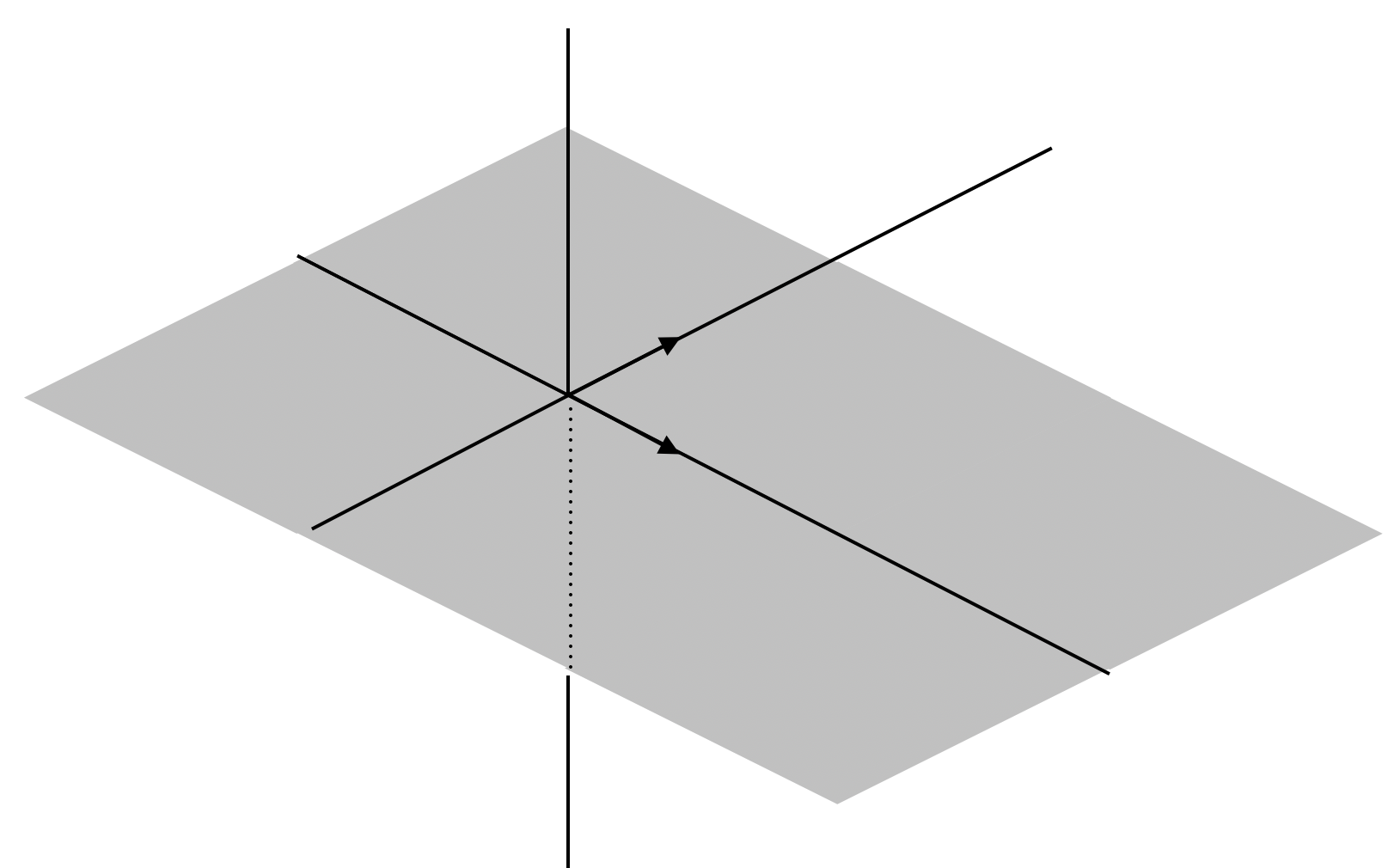
즉 3차원의 column vecotr 1개를 사용하면 것은 3차원의 공간 속에서 span이 직선의 형태를 띄게 되고 2개를 사용하면 평면의 형태를 가지게 된다. 그림으로 표현하지는 않았지만 3개의 column vector를 사용하면 span이 3차원 공간 전체를 차지하게 된다.

Span의 기하학적 형태를 생각하면 Linear Combination과 연립 방정식의 해의 유무가 조금 더 직관적으로 이해된다. 다시 말해 식

\[x_1 \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} + x_2 \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} = \begin{bmatrix} b_1\\ b_2\\ b_3 \end{bmatrix}\]

에서 벡터 \(\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\)와 \(\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\)의 Span 상에 \(\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}\)이 존재한다면 해가 존재한다고 할 수 있고, Span 밖에 존재한다면 해가 존재하지 않는다고 할 수 있다.

예를 들어

\[\begin{bmatrix} 1 && 0 \\ 0 && 1 \\ 0 && 0 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 3\\ 1\\ 0 \end{bmatrix}\]

의 해는 다음과 같이 표현되며, 첫 번째 column vector가 3번 사용되었고 두 번째 column vector가 1번 사용되었으므로 \(x_1 = 3\)이고 \(x_2 = 1\)이 된다.

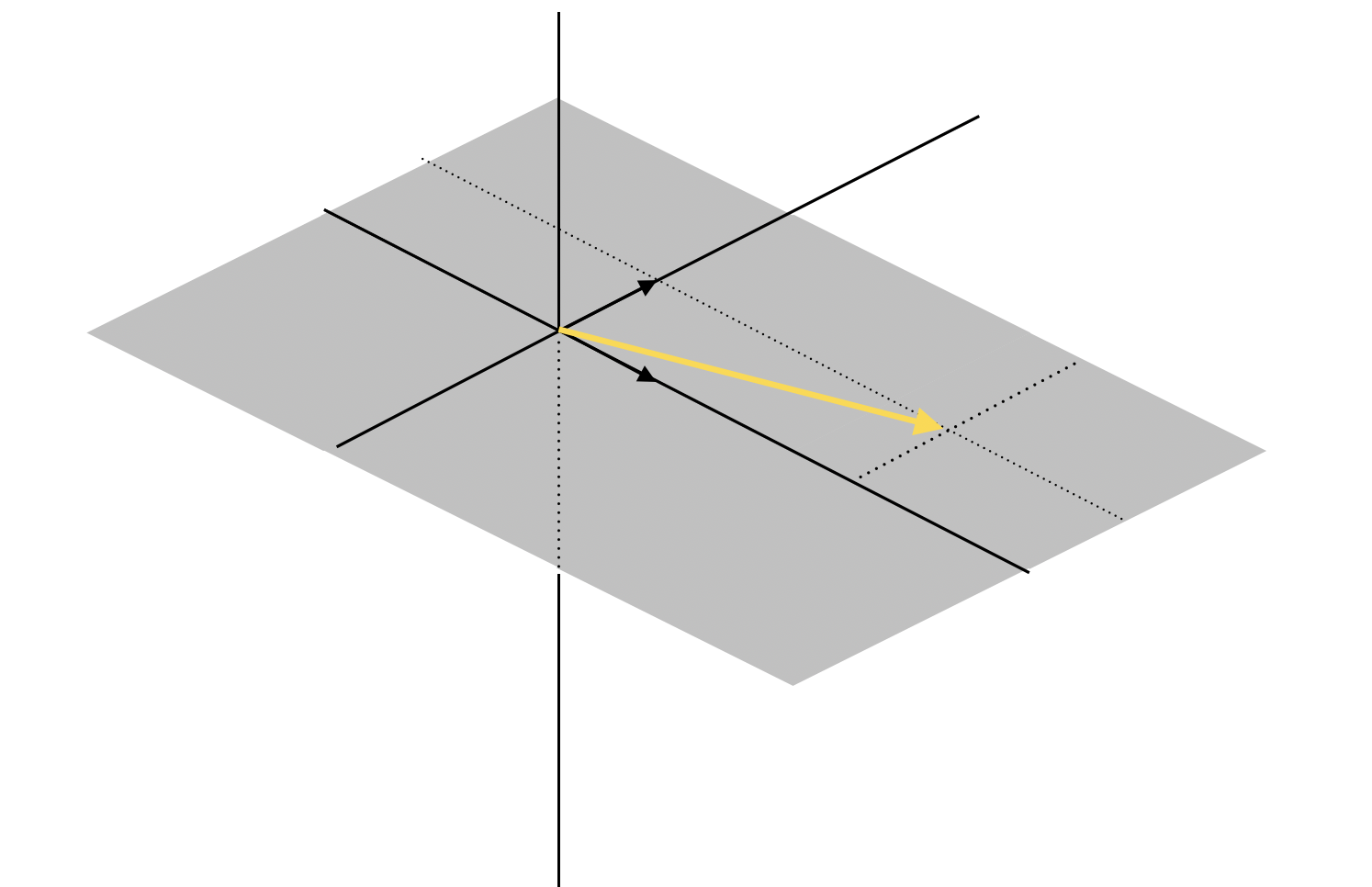
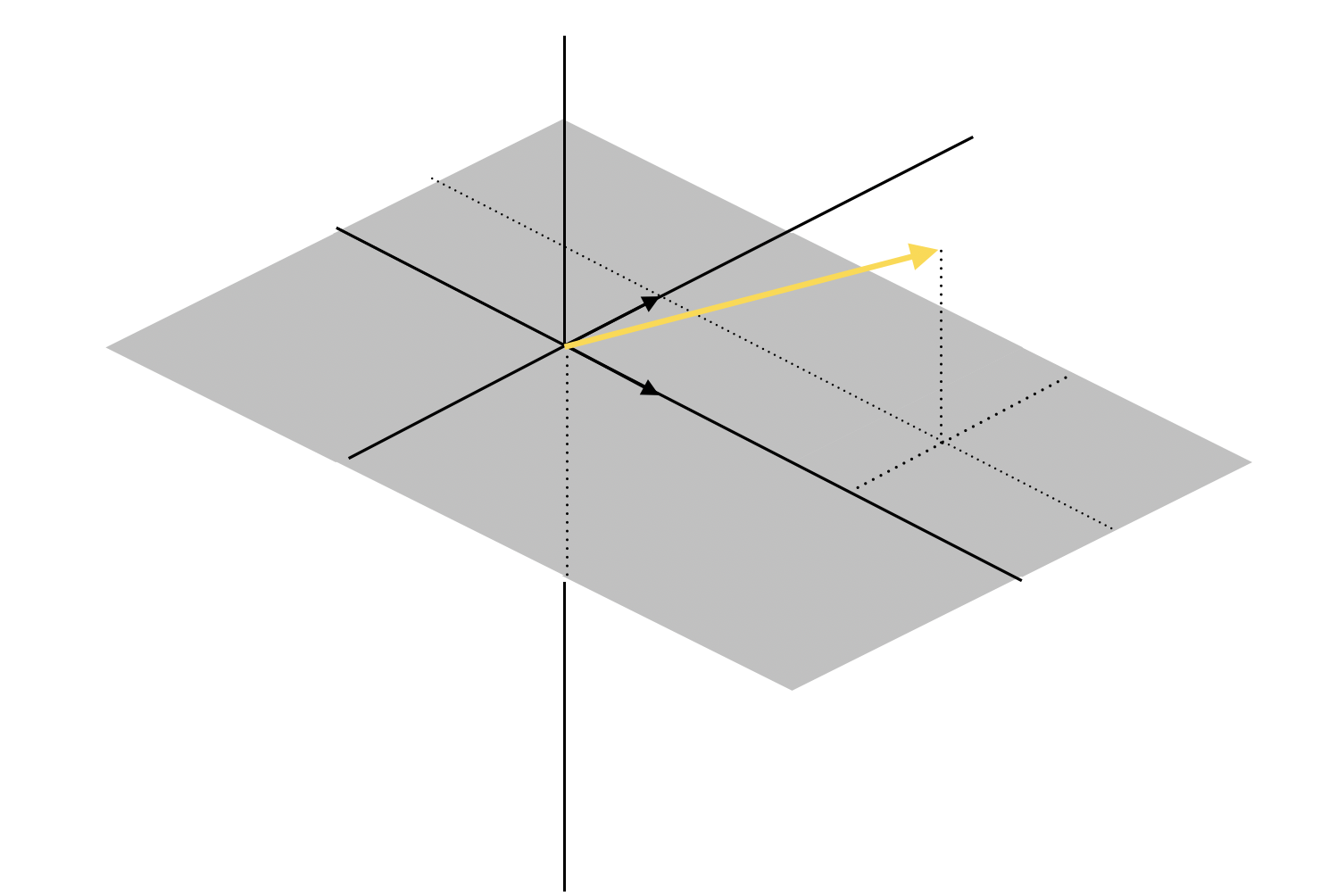
하지만 아래 그림과 같이 Span 밖에 위치하는 vector \(\begin{bmatrix} 3\\ 1\\ 2 \end{bmatrix}\)는 주어진 두 column vector로 표현할 수 없으므로 해가 존재하지 않는다.

Linear Independence

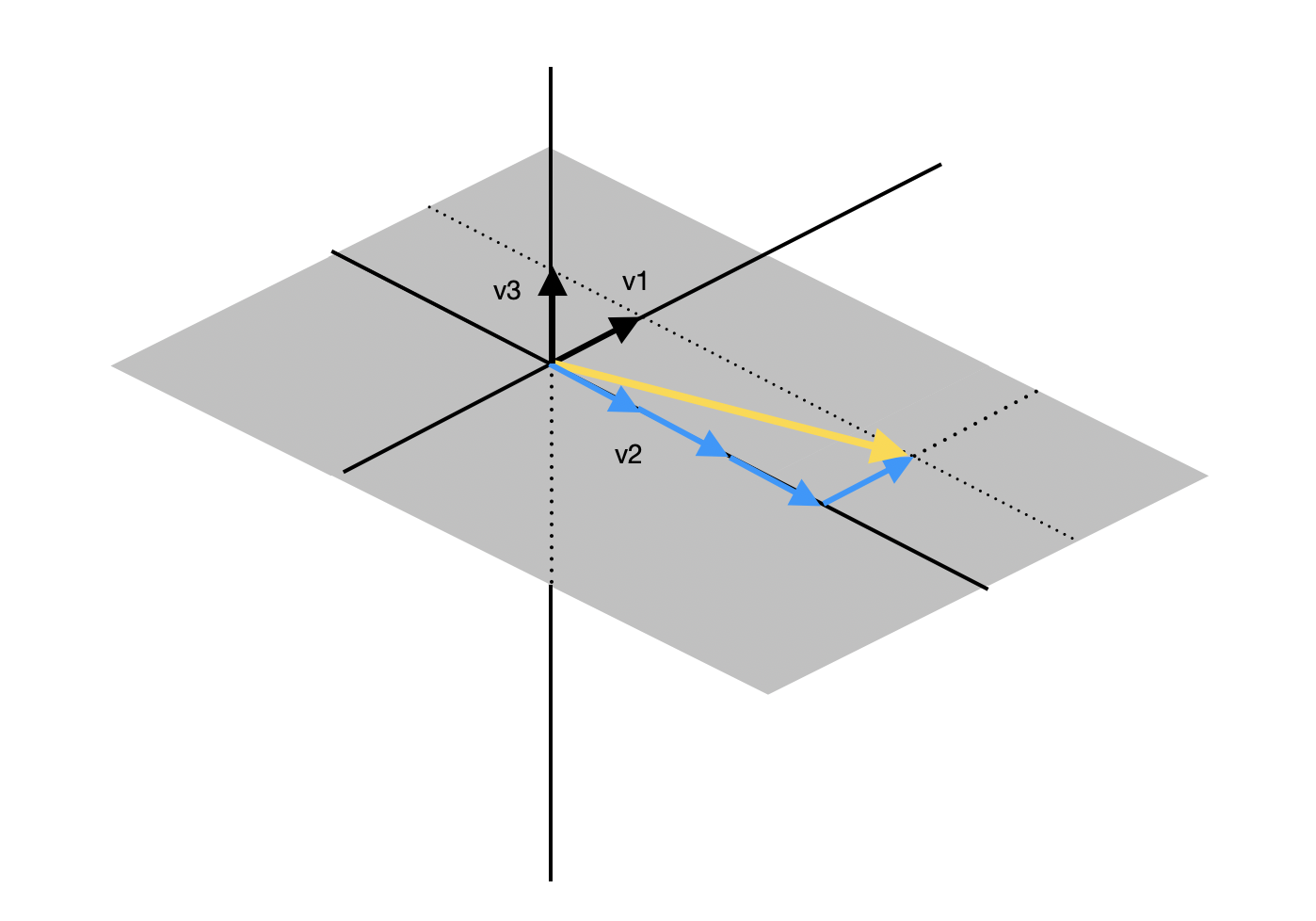
column vector가 3차원이고, 세 개의 column vector가 주어져 있다면 span 또한 3차원이 될 수 있다. 하지만 경우에 따라서는 span이 2차원에 머무를 수 있는데, 아래와 같이 세 개의 column vector가 모두 하나의 평면 상에 존재하는 경우이다.

이미지

위의 그림은 \(v_1, v_2, v_3\)의 span이지만 span의 크기는 \(v_1, v_2\)와 동일하다. 즉, 기존 vector \(v_1, v_2\)의 선형 결합으로 새로운 vector \(v_3\)을 표현할 수 있다. 이와 같이 vector가 추가되었음에도 span의 크기가 계속 유지되는 경우를 선형 의존(Linear Dependence)라고 한다. 반대로 vector의 추가로 인해 span의 크기가 커지는 경우를 선형 독립(Linear Independence)라고 한다.

Unique Solution

column vector 간의 관계가 선형 독립인지, 선형 의존인지 중요한 이유는 이것이 해의 갯수와 관련되기 때문이다. 정답부터 이야기하자면 선형 독립인 경우에만 해가 유일하다.

case 1: Linear Dependence

\[\boldsymbol{v_1} = \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix} \qquad \boldsymbol{v_2} = \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} \qquad \boldsymbol{v_3} = \begin{bmatrix} 1\\ 1\\ 0 \end{bmatrix}\]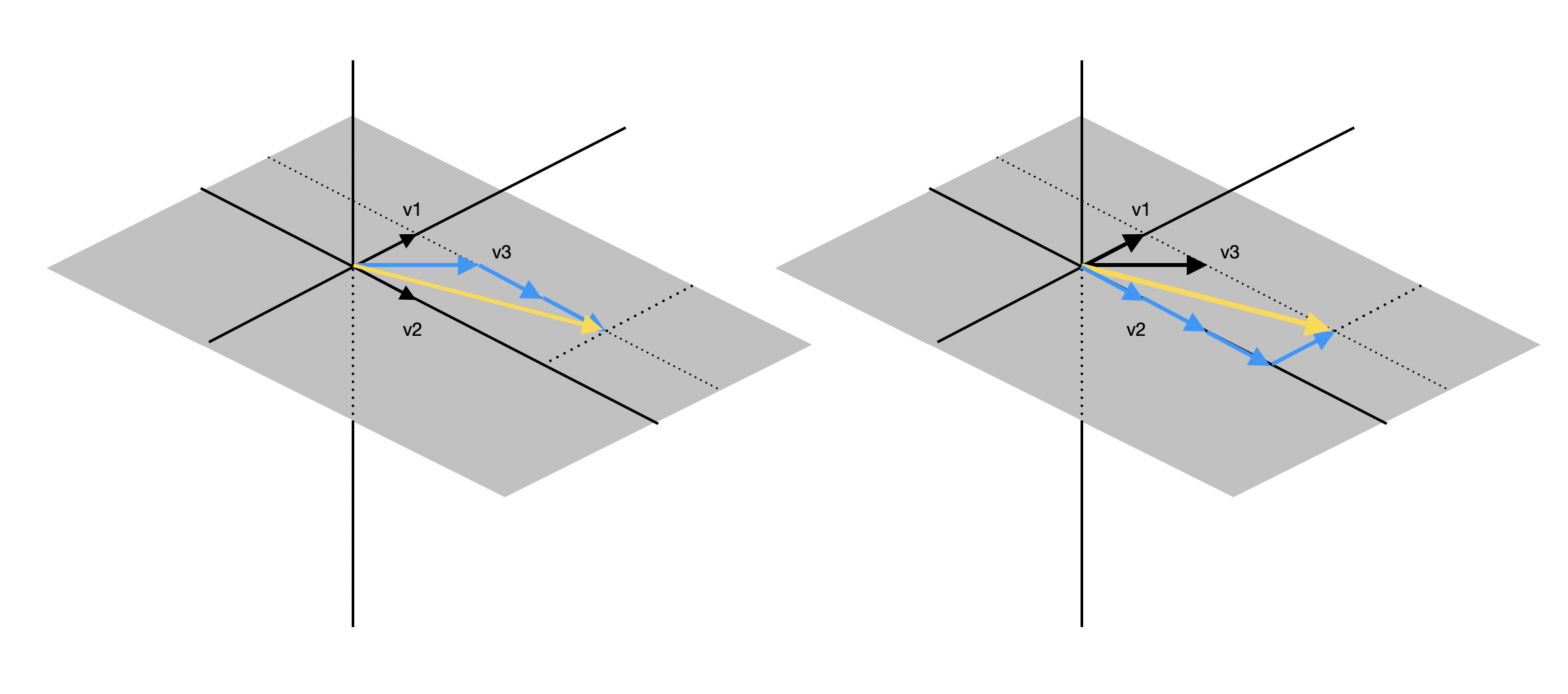

case 2: Linear Independence

\[\boldsymbol{v_1} = \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix} \qquad \boldsymbol{v_2} = \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} \qquad \boldsymbol{v_3} = \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}\]