Linear Algebra Introduction
- Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book과 주재걸 교수님의 강의 인공지능을 위한 선형대수를 듣고 작성했습니다.
- update at : 2020.07.08, 2020.09.26
Linearity
선형대수에서 선형(Linear)은 “직선의 형태”를 말한다. 즉 선형대수란 직선의 형태를 띄고 있는 것에 관한 대수학이라고 할 수 있다. 수학적으로 선형성(linearity)이란 어떤 함수 \(f\)가 임의의 원소 \(x, y, a\)에 대해 다음 두 조건을 만족하는 경우를 말한다.
\[\eqalign{ &1. \ f(ax) = af(x) \\ &2. \ f(x+y) = f(x) + f(y) }\]예를 들어 1차 함수 \(y = 6x\)가 선형성을 가지는지 확인해본다면,
\[\eqalign{ &1. \ 6(ax) = a(6x) \\ &2. \ 6(x+y) = 6x + 6y }\]와 같이 두 가지 조건을 모두 만족한다. 따라서 선형성을 가진다고 할 수 있다.
반면 2차 함수 \(y = 2x^2\)의 경우
\[\eqalign{ &1. \ 2(ax)^2 \ne a 2(x)^2 \\ &2. \ 2(x+y)^2 \ne 2x^2 + 2y^2 }\]두 가지 조건을 모두 만족하지 않으므로 선형성을 가진다고 할 수 없다. 2차 함수의 모양을 생각해 보더라도 선형과는 거리가 있어 보인다.
그런데 직선의 형태를 가지는 1차 함수의 경우에도 \(y = 6x + 2\) 와 같이 원점을 지나지 않는 경우에는 선형성을 가지지 않는다.
\[\eqalign{ & 1. \ 6(ax) + 1 \ne a(6x + 2) \\ & 2. \ 6(x+y) + 2 \ne 6x + 2 + 6y + 2 }\]즉 다항함수의 경우 1차함수 중에서도 원점 \((0,0)\)을 지나는 경우에만 선형성을 가진다고 할 수 있다.
Scalar, Vector and Matrix
선형대수의 기본적인 구성요소들로는 scalar, vector, matrix가 있다.
1) scalar
scalar는 단일 숫자를 말한다. 방향은 나타내지 않고 크기만을 갖는다.
2) vector
Deep Learning book에서는 vector를 “an array of numbers”, 즉 숫자들의 배열이라고 정의한다. vector를 구성하는 각각의 숫자(element)들을 제각기 다른 축에서의 크기라고 생각하면 vector는 어떤 공간 상에서의 한 점(point)를 의미한다.
\[\boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \\ ... \\ x_n \end{bmatrix}\]3) matrix
matrix는 “a 2-D array of numbers”로 정의된다. 즉 여러 개의 vector를 붙여둔 것이라고 이해할 수 있다. 2차원이므로 matrix는 높이와 너비를 가지는데, 이때 높이가 m이고 너비가 n인 matrix \(A\)를 \(A \in \rm l\!R^{m \times n}\)으로 표기한다.
\[\boldsymbol{A} = \begin{bmatrix} a_{1,1} && a_{1,2} && ... && a_{1,n}\\ a_{2,1} && a_{2,2} && ... && a_{2,n}\\ ... && ... && ... && ... \\ a_{m,1} && a_{m,2} && ... && a_{m,n}\\ \end{bmatrix}\]참고로 scalar는 소문자, vector는 두꺼운 소문자, matrix는 대문자로 표기한다.
Properties of Vector
구체적으로 벡터는 다음 8가지의 특성을 가저야 한다.
\[\eqalign{ &1. \qquad \boldsymbol{u} (\boldsymbol{v} + \boldsymbol{w}) = (\boldsymbol{u} + \boldsymbol{v}) + \boldsymbol{w} \\ &2. \qquad \boldsymbol{u} + \boldsymbol{v} = \boldsymbol{v} + \boldsymbol{u} \\ &3. \qquad \boldsymbol{u} + \boldsymbol{0} = \boldsymbol{u} \\ &4. \qquad \boldsymbol{u} + (- \boldsymbol{u}) = \boldsymbol{0}\\ &5. \qquad \alpha (\boldsymbol{u} + \boldsymbol{v}) = \alpha \boldsymbol{u} + \alpha \boldsymbol{v} \\ &6. \qquad (\alpha + \beta) \boldsymbol{u} = \alpha \boldsymbol{u} + \beta \boldsymbol{u} \\ &7. \qquad \alpha(\beta \boldsymbol{u}) = (\alpha \beta) \boldsymbol{u} \\ &8. \qquad 1 \cdot \boldsymbol{u} = \boldsymbol{u} }\]Geometrical meaning of vector
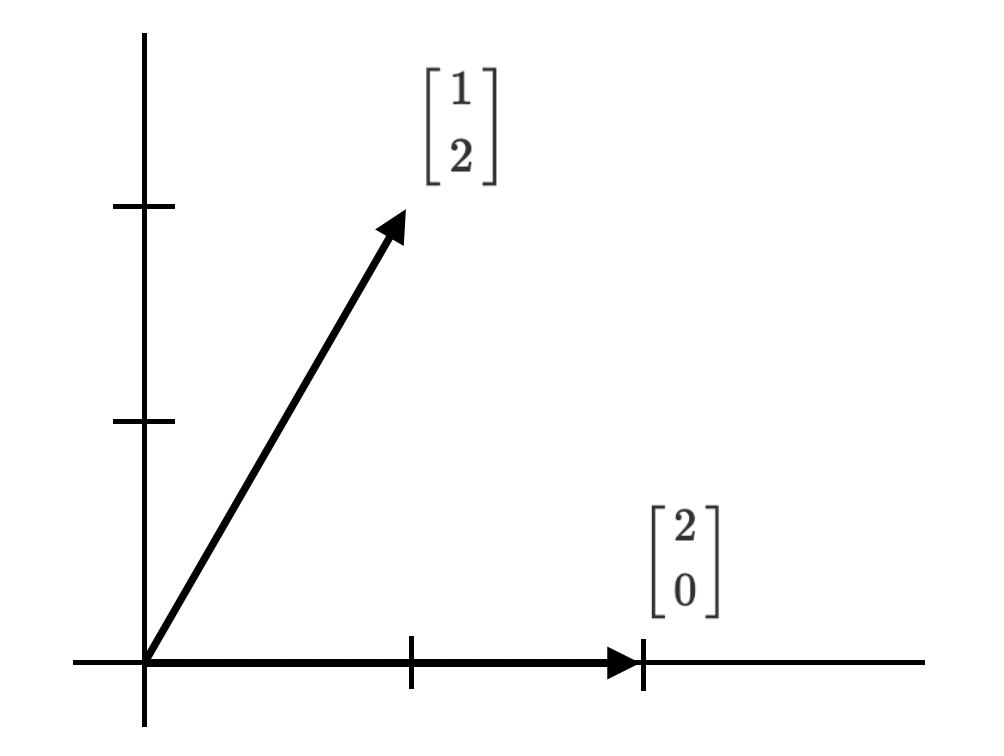
선형대수는 벡터 공간을 가정하고 그 속에서 이뤄지는 벡터간 연산에 관한 것이라고 할 수 있다. 벡터 공간이란 쉽게 말해 좌표계인데 2차원 공간에서 벡터 \(\begin{bmatrix} 1\\2 \end{bmatrix}, \begin{bmatrix} 2\\0 \end{bmatrix}\) 은 다음과 같이 크기와 방향을 가진 화살표로 표현된다.
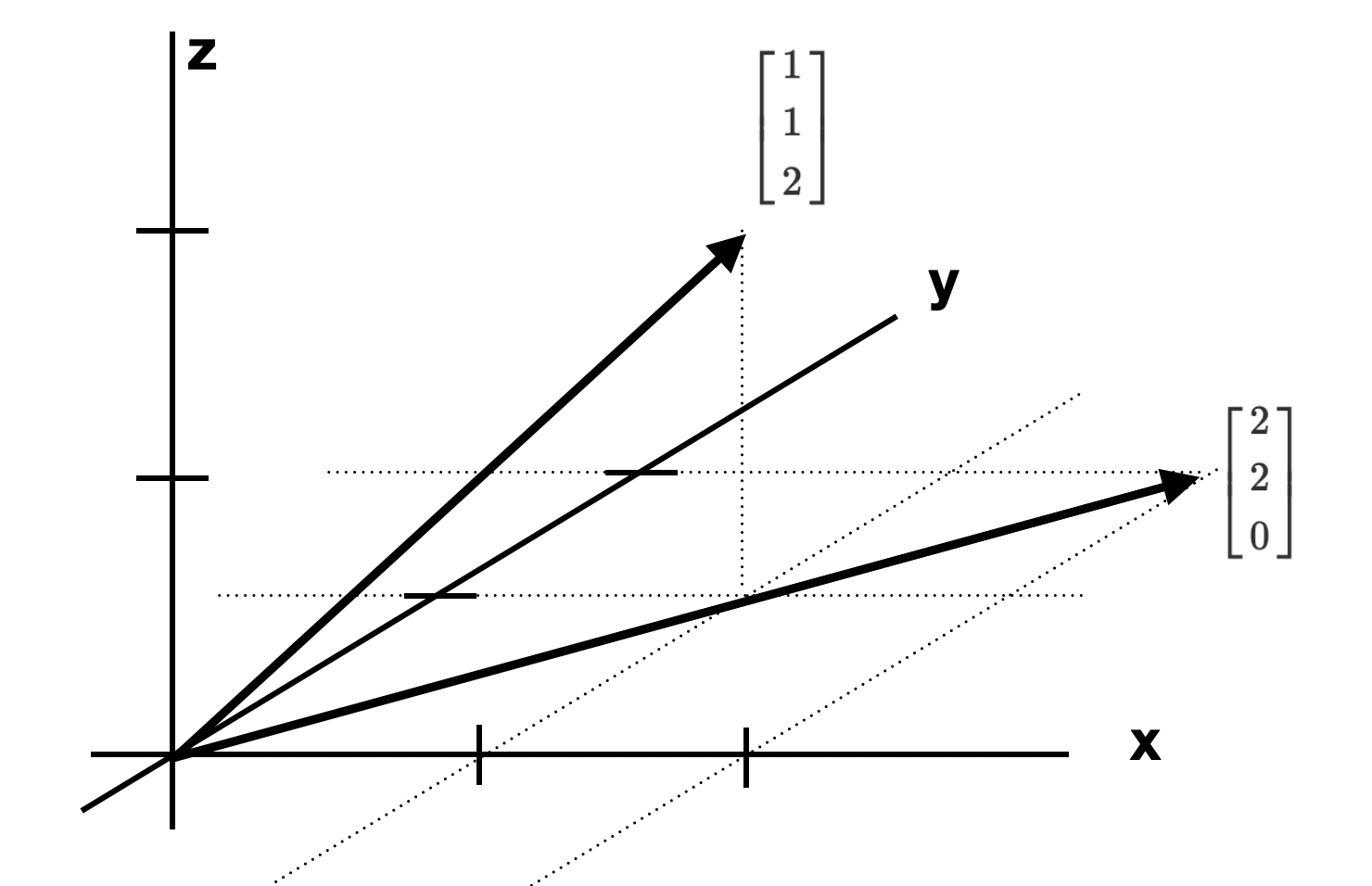
3차원 공간에서도 가능하다. \(\begin{bmatrix} 1\\1\\2 \end{bmatrix}, \begin{bmatrix} 2\\2\\0 \end{bmatrix}\)의 경우 아래 그림과 같다. 4차원, 그 이상도 가능하지만 평면의 그림으로 그리기에는 어려움이 있다.
벡터 간의 덧셈이 이뤄지는 과정은 다음과 같이 평행사변형 꼴로 표현된다.
\[\begin{bmatrix} 1\\2 \end{bmatrix} \ + \ \begin{bmatrix} 2\\0 \end{bmatrix} = \ \begin{bmatrix} 3\\2 \end{bmatrix}\]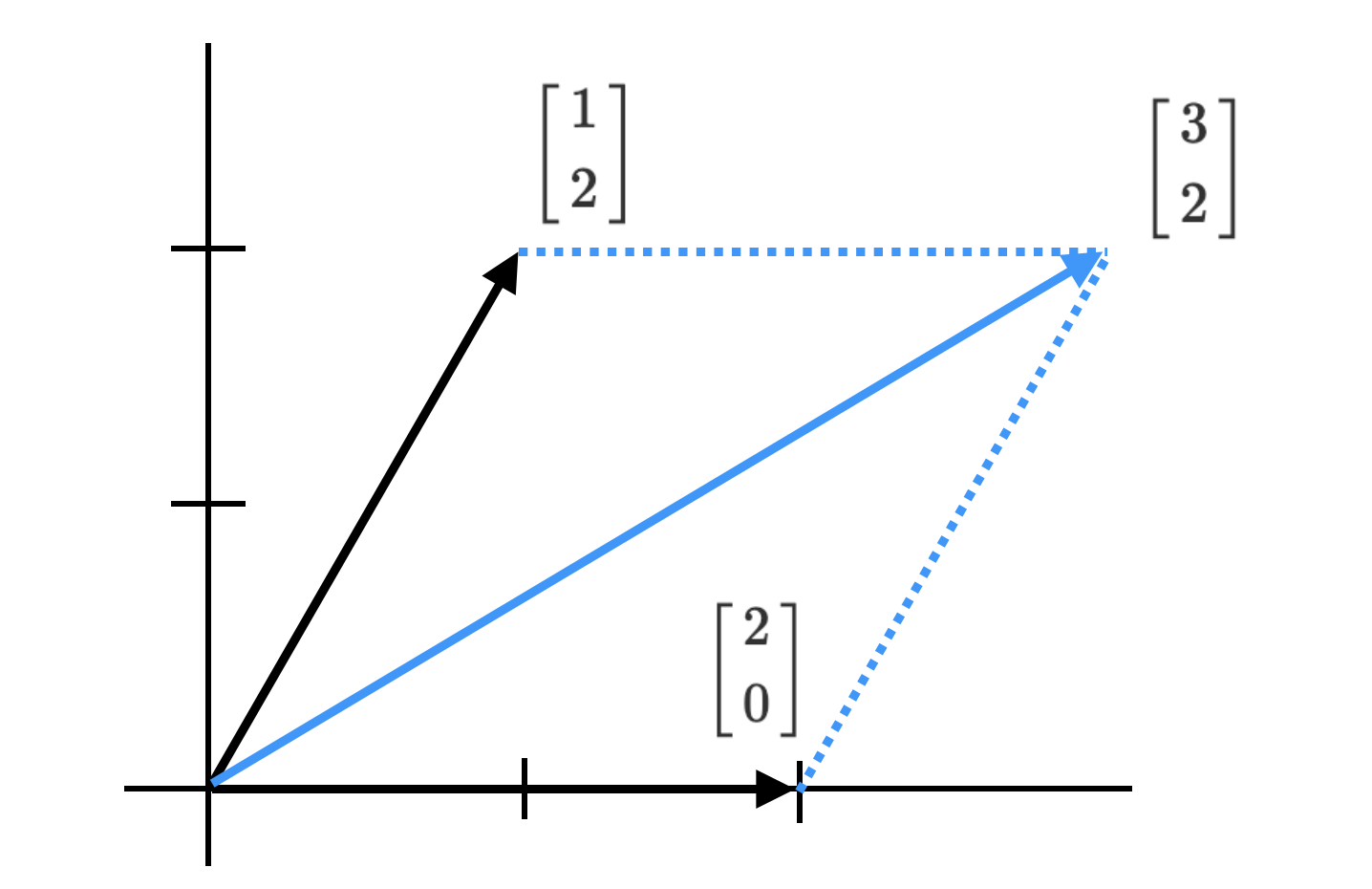
Linear Equation
아래와 같은 형태를 갖는 방정식을 선형 방정식(linear equation)이라고 부른다.
\[a_1x_1 + a_2x_2 + ... + a_nx_n = b\]위와 같은 선형 방정식은 선형대수의 구성요소인 Vector들 간의 곱으로 보다 간단하게 나타낼 수 있다.
\[\boldsymbol{a}^T \boldsymbol{x} = b \qquad when \ \boldsymbol{a} = \begin{bmatrix} a_1 \\ a_2 \\ ... \\ a_n \end{bmatrix}, \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \\ ... \\ x_n \end{bmatrix}\]연립 선형 방정식 또한 선형대수에서는 보다 간단하게 표현할 수 있다. 아래와 같은 연립 선형 방정식은
\[a_{11}x_1 + a_{12}x_2 + a_{13}x_3 = b_{1}\\ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 = b_2\\ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 = b_3\\\]vector와 matrix를 사용하여 간단하게 표현할 수 있다.
\[\boldsymbol{A} \boldsymbol{x} = \boldsymbol{b} \qquad when \ \boldsymbol{A} = \begin{bmatrix} a_{11} && a_{12} && a_{13} \\ a_{21} && a_{22} && a_{23} \\ a_{31} && a_{32} && a_{33} \\ \end{bmatrix}, \ \boldsymbol{x} = \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}, \boldsymbol{b} = \begin{bmatrix} b_1\\ b_2\\ b_3 \end{bmatrix}\]Inverse Matrix
위와 같은 방정식의 해를 구하는 것은 곧 matrix \(A\)의 역행렬(Inverse Matrix)을 구하는 것과 같다. 역행렬이란 아래 식과 같이 원행렬과 곱했을 때 항등행렬(Identity Matrix)가 되는 것을 말한다.
\[\boldsymbol{A^{-1}} \boldsymbol{A} = \boldsymbol{A} \boldsymbol{A^{-1}} = \boldsymbol{I}\]Identity Matrix
항등행렬(단위행렬)은 아래와 같이 대각 원소는 모두 1이고 이외 다른 원소는 모두 0인 정방행렬을 의미한다.
\[\boldsymbol{I} = \begin{bmatrix} 1 && 0 && 0\\ 0 && 1 && 0\\ 0 && 0 && 1\\ \end{bmatrix}\]항등행렬은 행렬 간 곱셈 연산에 있어 항등원의 성질을 띈다. 즉 \(AI = IA = A\) 이 성립한다.
Inverse Matrix and Linear Equation
선형 방정식 \(\boldsymbol{A} \boldsymbol{x} = b\)에 역행렬과 항등행렬의 특성을 적용하면 다음과 같이 \(\boldsymbol{x}\)를 구할 수 있다.
\[\eqalign{ &\boldsymbol{A} \boldsymbol{x} = \boldsymbol{b} \\ &\boldsymbol{A^{-1}}\boldsymbol{A} \boldsymbol{x} = \boldsymbol{A^{-1}}\boldsymbol{b} \\ &\boldsymbol{I} \boldsymbol{x} = \boldsymbol{A^{-1}}\boldsymbol{b} \\ &\boldsymbol{x} = \boldsymbol{A^{-1}}\boldsymbol{b}\\ }\]Inverse Matrix is not always available
\(\boldsymbol{A}\)에 대한 역행렬을 구할 수 있다면 쉽게 해를 찾을 수 있지만 그렇지 못한 경우도 많다. \(2 \times 2\) 정방행렬에서는 어떤 행렬 \(\boldsymbol{A}\)에 대한 역행렬을 다음 공식에 따라 구할 수 있다.
\[\boldsymbol{A^{-1}} = {1 \over {ad - bc}} \begin{bmatrix} d && -b \\ -c && a\\ \end{bmatrix}\]이 경우 우변의 분모 \(ad - bc\)가 0이라면 역행렬을 구할 수 없는 상황이 된다. 이때 \(ad - bc\)를 역행렬의 존재 여부를 판단하는 식이라 하여 우리말로는 행렬식, 영어로는 determinant라고 하며 줄여서 \(det \boldsymbol{A}\)라고 표현하기도 한다. 참고로 역행렬을 구할 수 없다는 것은 연립 방정식의 해가 하나도 없거나, 무수히 많다는 것을 의미한다.
정방행렬이 아닌 직사각형 행렬(rectangular matrix)은 row의 개수와 column의 개수가 일치하지 않는 행렬을 의미한다. 위의 연립 방정식과 연결하여 생각해 본다면 식의 개수와 미지수의 개수가 일치하지 않는 경우라고 할 수 있다.
일반적으로 연립 방정식에서 구하고자 하는 미지수의 개수보다 식의 개수가 더 많은 경우에는 해가 없고, 구하고자 하는 미지수의 개수보다 식의 개수가 적은 경우에는 해가 무수히 많아진다. 이러한 점을 생각해 볼 때 직사각형 행렬 \(\boldsymbol{A}\)의 row의 개수가 column의 개수보다 작은 경우에는 해가 없고, row의 개수가 column의 개수보다 큰 경우에는 해가 무수히 많다고 할 수 있다.