Universal Approximation Experiment
- Reference
- paper review
- Update at: 2020.10.23
Universal Approximation Theorem
Universal Approximation Theorem은 하나의 뉴럴 네트워크 레이어와 임의의 연속적인 시그모달 비선형 활성함수(Arbitrary Continuous Sigmoidal Nonlinearity)만으로도 \(n\)차원의 unit cube \([0,1]^n I_n\) 상의 모든 연속함수를 충분히 근사(Approximate)할 수 있다는 것에 대한 수학적인 증명이다. 명제만 보면 다소 복잡하지만 쉽게 말해 딥러닝 모델로 모든 연속함수를 모사할 수 있다는 것을 의미하며, 이러한 점에서 딥러닝의 가장 기초가 되는 이론 중 하나다.
하나의 뉴럴 네트워크 레이어 만으로도 세상의 모든 연속함수를 모사하기에 충분하다는 것은 매우 강력한 명제이다. 하지만 ‘충분’하다는 표현에 함정이 있다. 이상과 현실의 괴리라고도 할 수 있는데 이상적으로는 ‘충분’하다고 하지만 현실적으로 ‘충분’한 수준에 도달하는 것은 매우 어려울 수 있기 때문이다. 만약 하나의 레이어 만으로도 쉽게 모든 연속함수를 모사할 수 있다면 딥러닝과 관련하여 지금과 같이 무수히 많은 논문들이 나올 필요도 없었을 것이다.
Experiment Setting
본 포스팅에서는 뉴럴 네트워크로 다양한 함수들을 모사하도록 하여 딥러닝 모델이 얼마나 근사를 잘하는지 확인해 보고자 한다. 다만 Universal Approximation Theorem에서는 하나의 레이어를 가정하지만 두 개 이상의 레이어에 대해서만 실험을 진행하였다. 모든 딥러닝 모델은 \(f: A \subset \mathcal R^1 \rightarrow \mathcal R^1\) 함수로, 스칼라 값을 입력으로 받아 스칼라 값을 예측하는 것을 목표로 한다.
Model
- 2 Layer Model
self.net = nn.Sequential(
nn.Linear(1, 512),
nn.LeakyReLU(),
nn.Linear(512, 1),
)
- 3 Layer Model
self.net = nn.Sequential(
nn.Linear(1, 512),
nn.LeakyReLU(),
nn.Linear(512, 64),
nn.LeakyReLU(),
nn.Linear(64, 1),
)
Data
모사하고자 하는 함수는 다음 네 가지이다. 모든 함수의 Domain은 \([1e-6, 100]\)이고, 여기서 등간격으로 10,000개의 샘플을 뽑아 데이터 셋을 구성했다.
| Name | Function |
|---|---|
| Log 함수 | \(y = log(x)\) |
| Polynomial 함수 | \(y=0.0001 x^2 - 0.001 x + 0.8\) |
| Sin 함수 | \(y = \sin (x)\) |
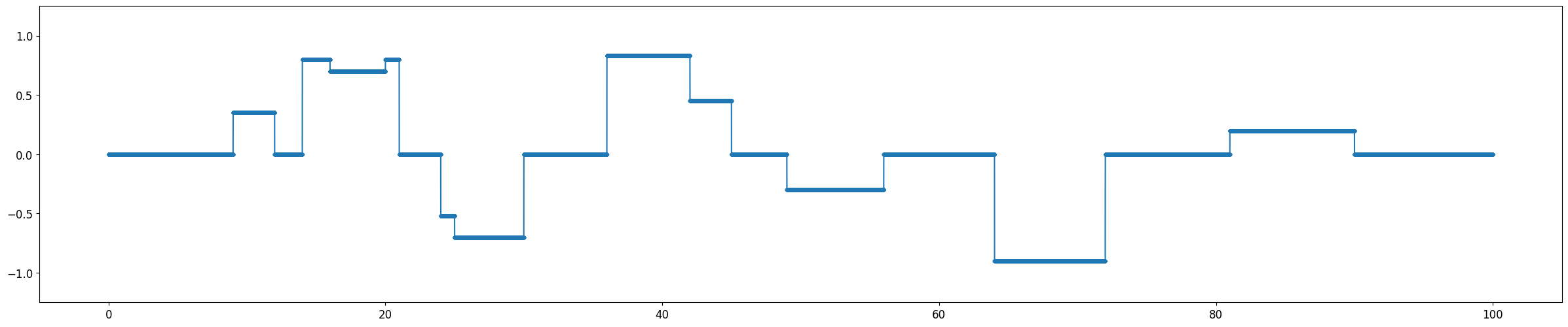
| Discrete 함수 | plot 참조 |
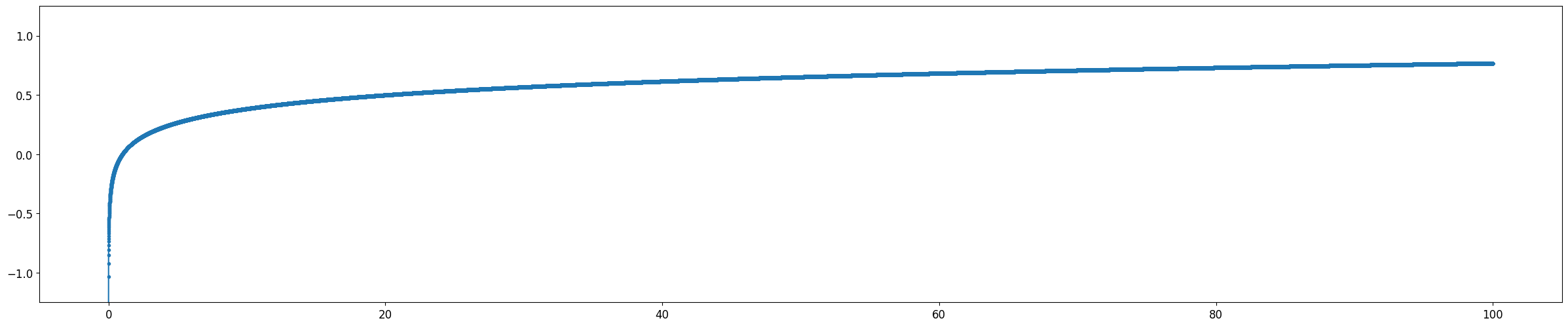
Log Function
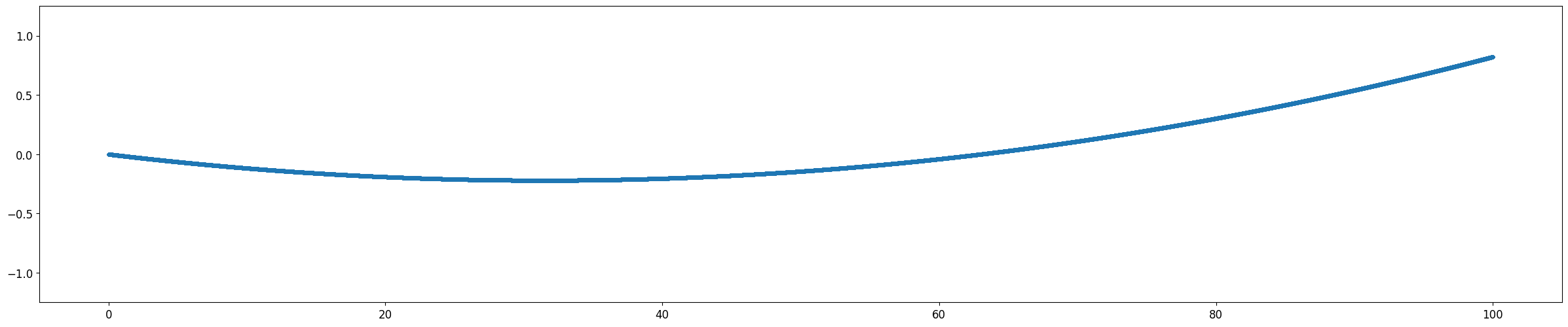
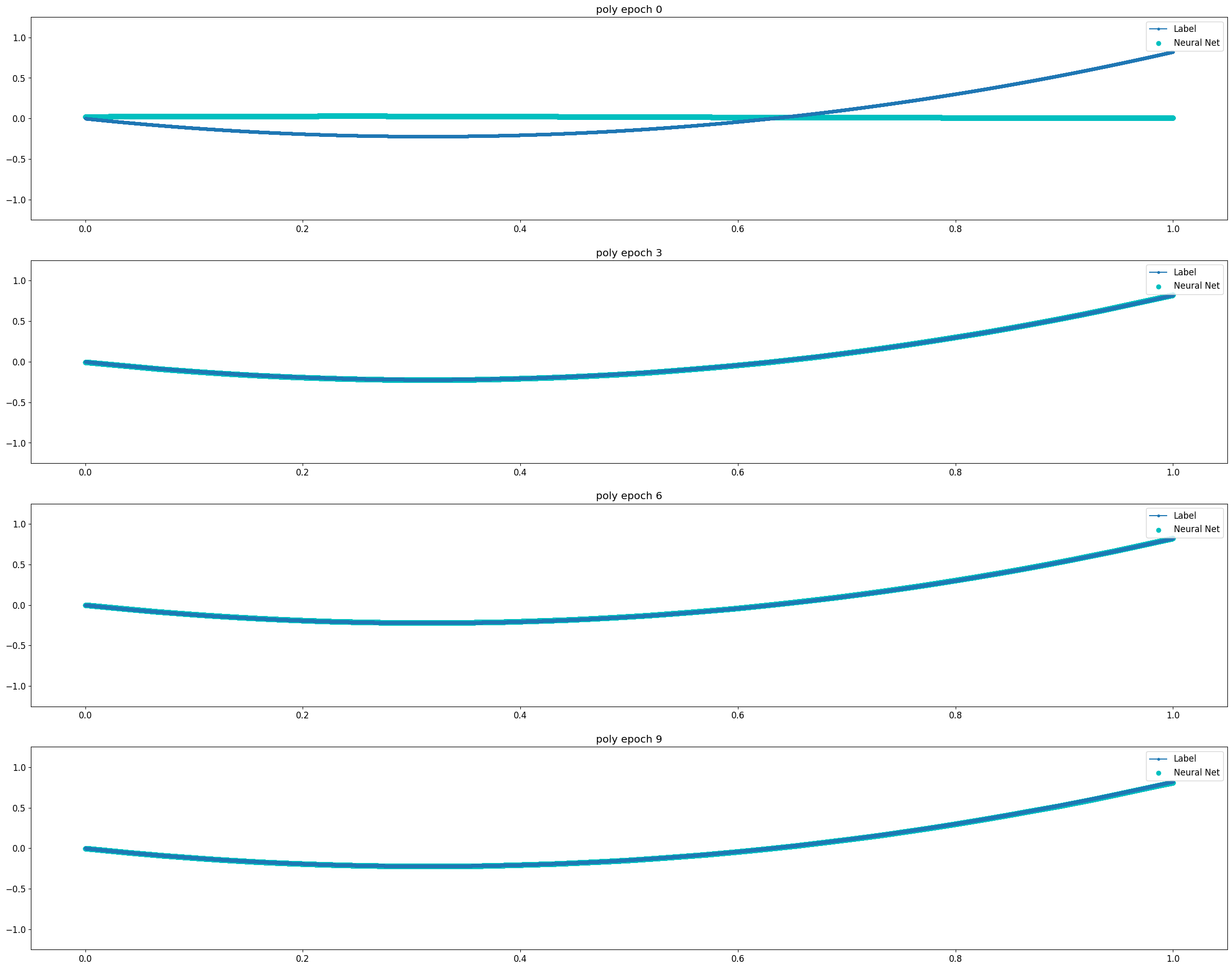
Polynomial Function
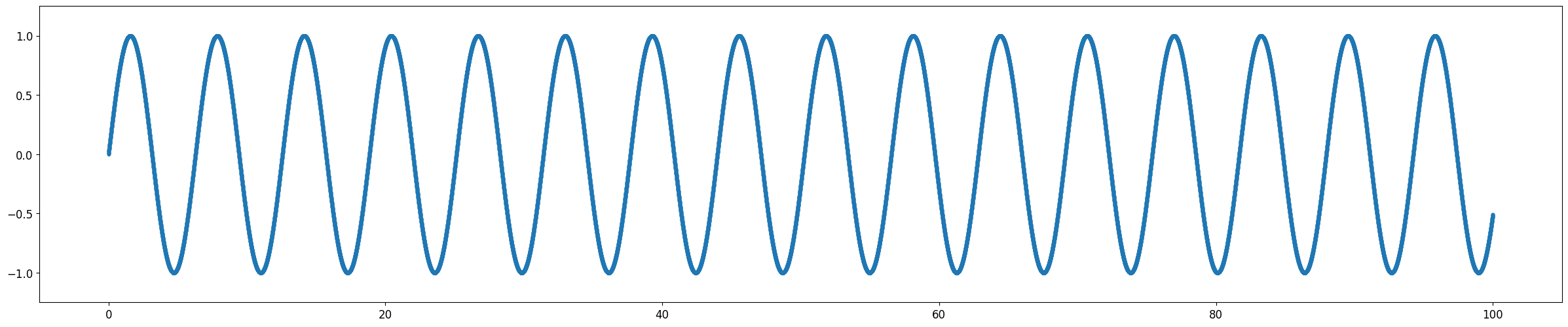
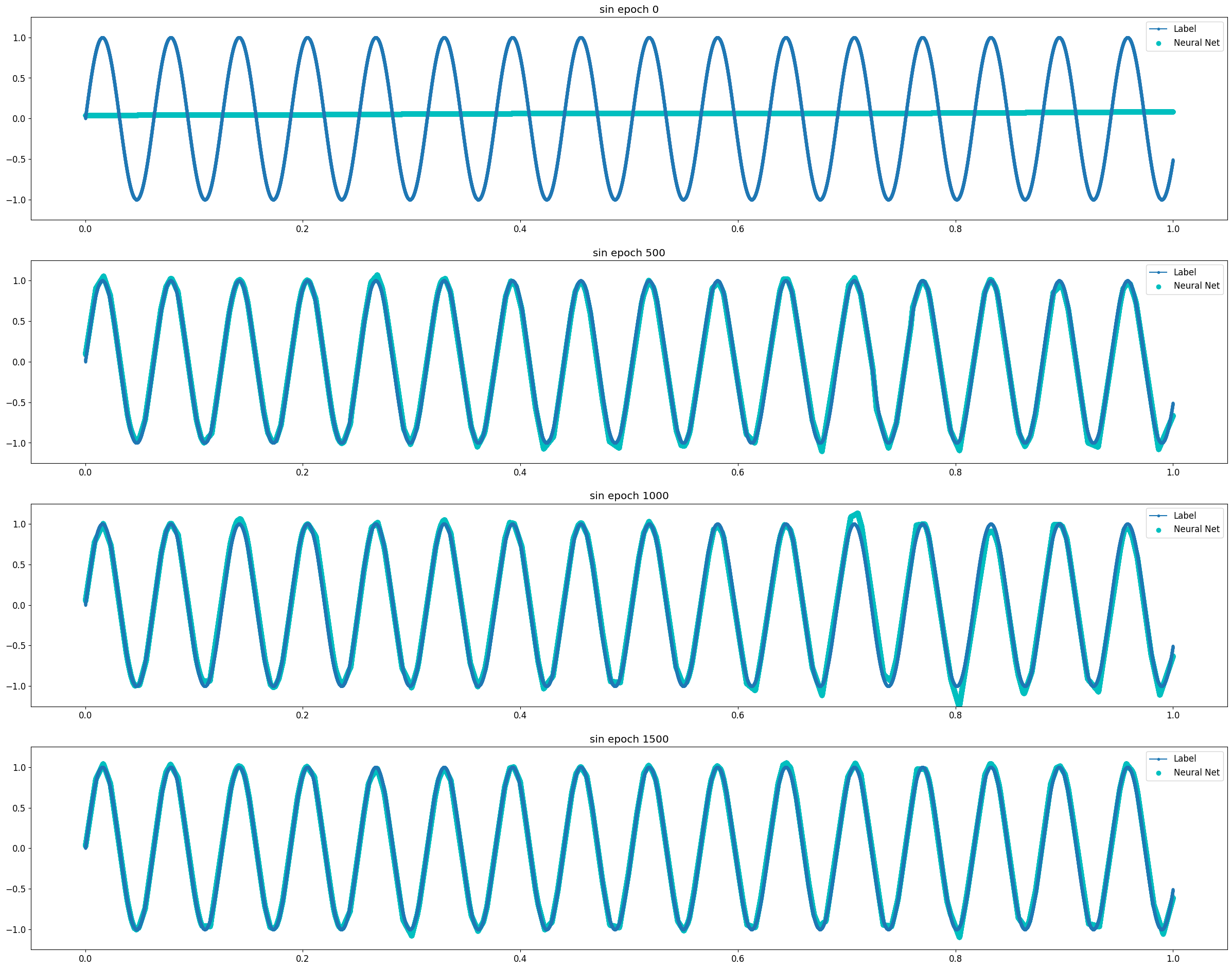
Sin Function
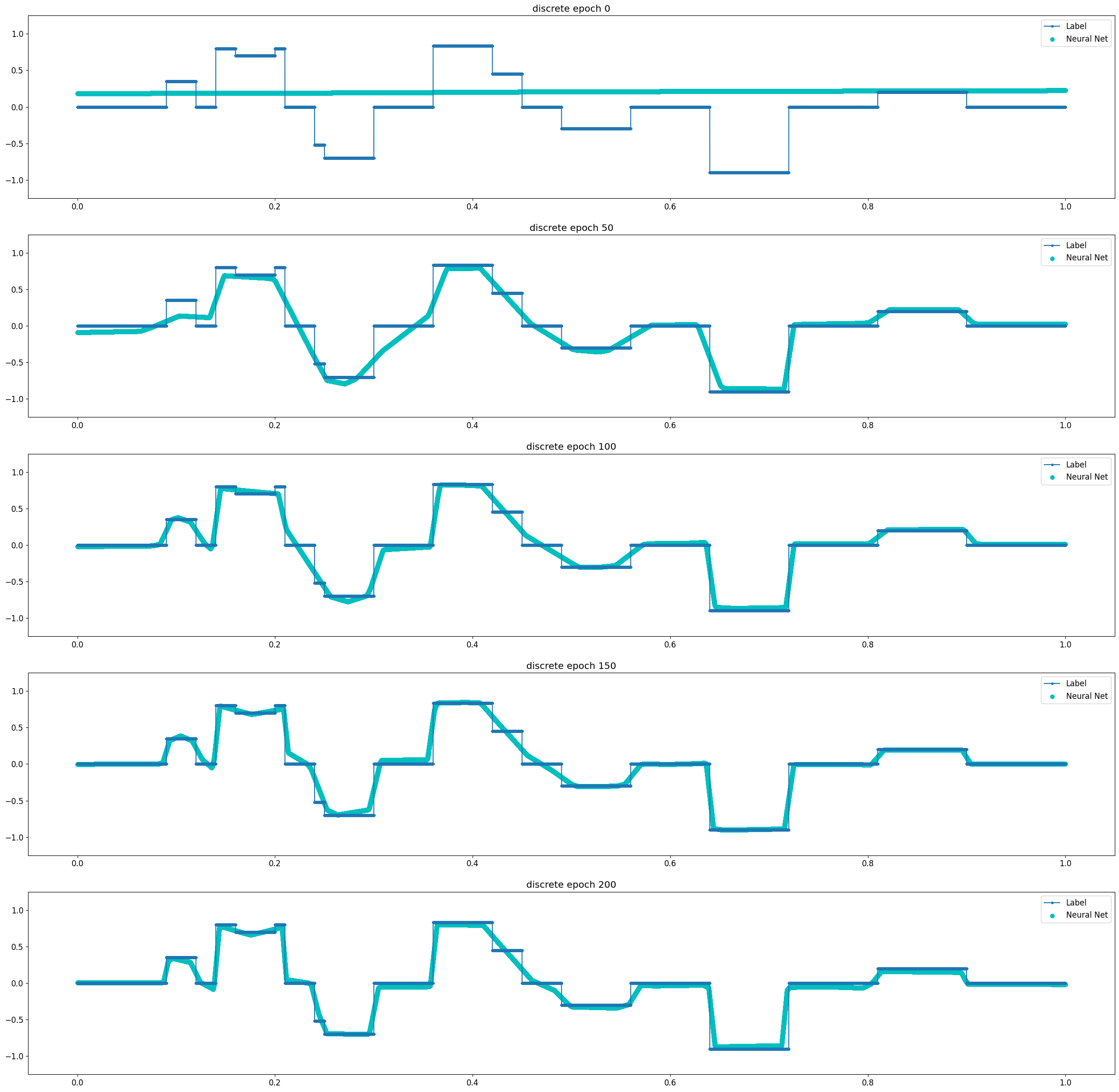
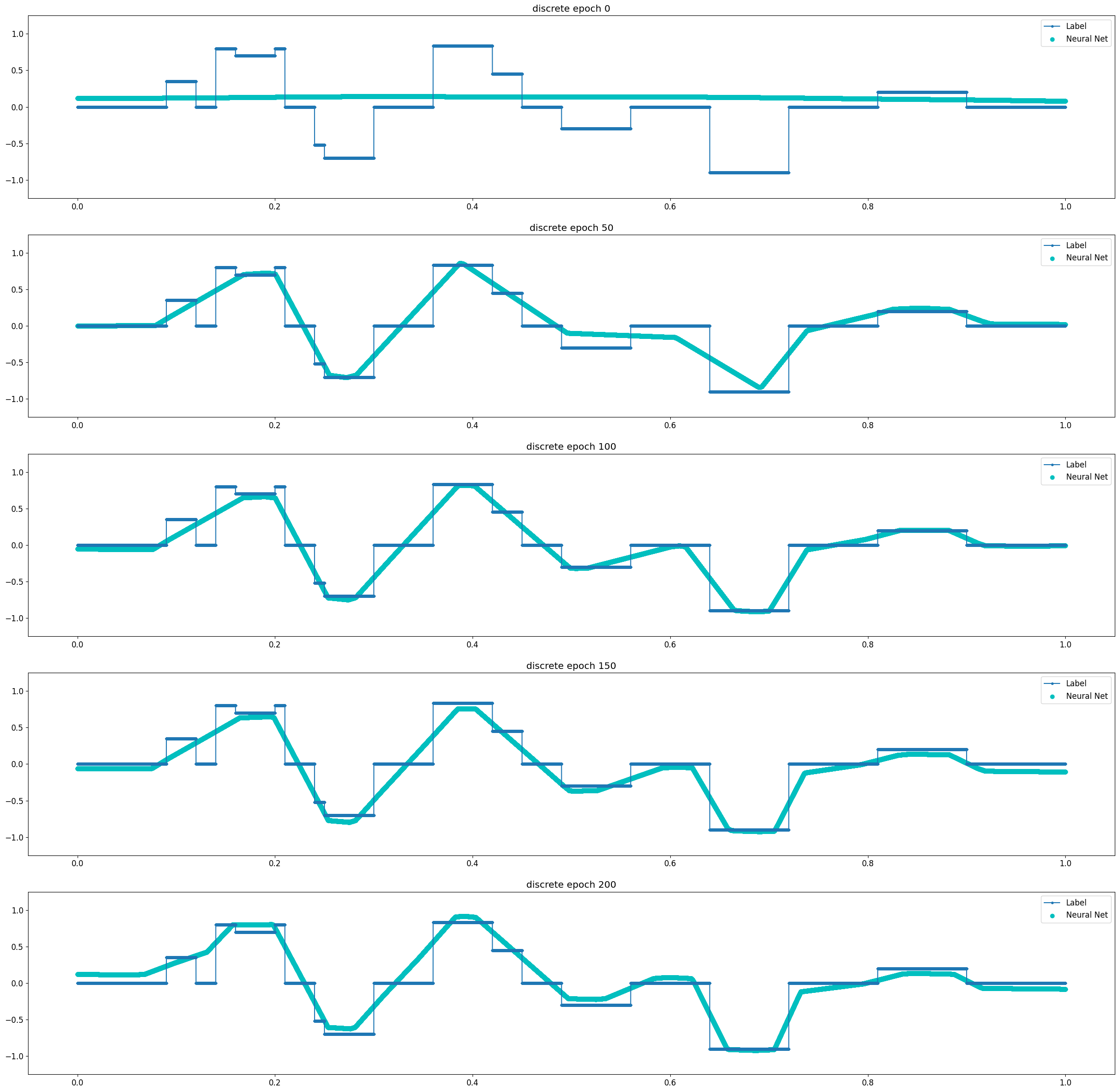
Discrete Function
Results
실험의 결과는 다음과 같이 두 가지로 정리할 수 있다.
Looks Like Continuous Function
Universal Approximation Theorem은 뉴럴 네트워크로 연속 함수를 모사할 수 있다는 것에 대한 이론이다. 비교적 단순한 연속 함수인 Log 함수와 3차 Polynomial 함수의 경우 2 Layer Model에서도 10 Epoch 이내에 매우 빠르게 근사함을 확인할 수 있었다. 같은 연속함수이지만 파동성이 큰 Sin 함수의 경우 1500 Epoch까지도 근사의 정확도가 떨어졌다. Discrete 함수는 학습이 진행됨에 따라 연속 함수의 형태로 최대한 근접하게 모사하려 한다는 것을 알 수 있다.
Depth and Overfitting
3 Layer의 경우 보다 빠르고 정확하게 모사함을 알 수 있다. 이러한 특성은 Sin 함수와 Discrete 함수와 같이 수렴하기 다소 어려운 경우에 도드라진다. 실험의 Task가 어떤 함수에 최대한 근사하고 싶은 것이므로 어떻게 보면 Overfitting이 목표라고 할 수 있다. 이러한 점에서 네트워크가 깊어지면 질수록 보다 복잡한 함수를 모사할 수 있음과 동시에 Overfitting 문제가 보다 쉽게 발생한다는 것으로도 해석이 가능하다.
Experiment 1) 2 Layer Model
Log Function
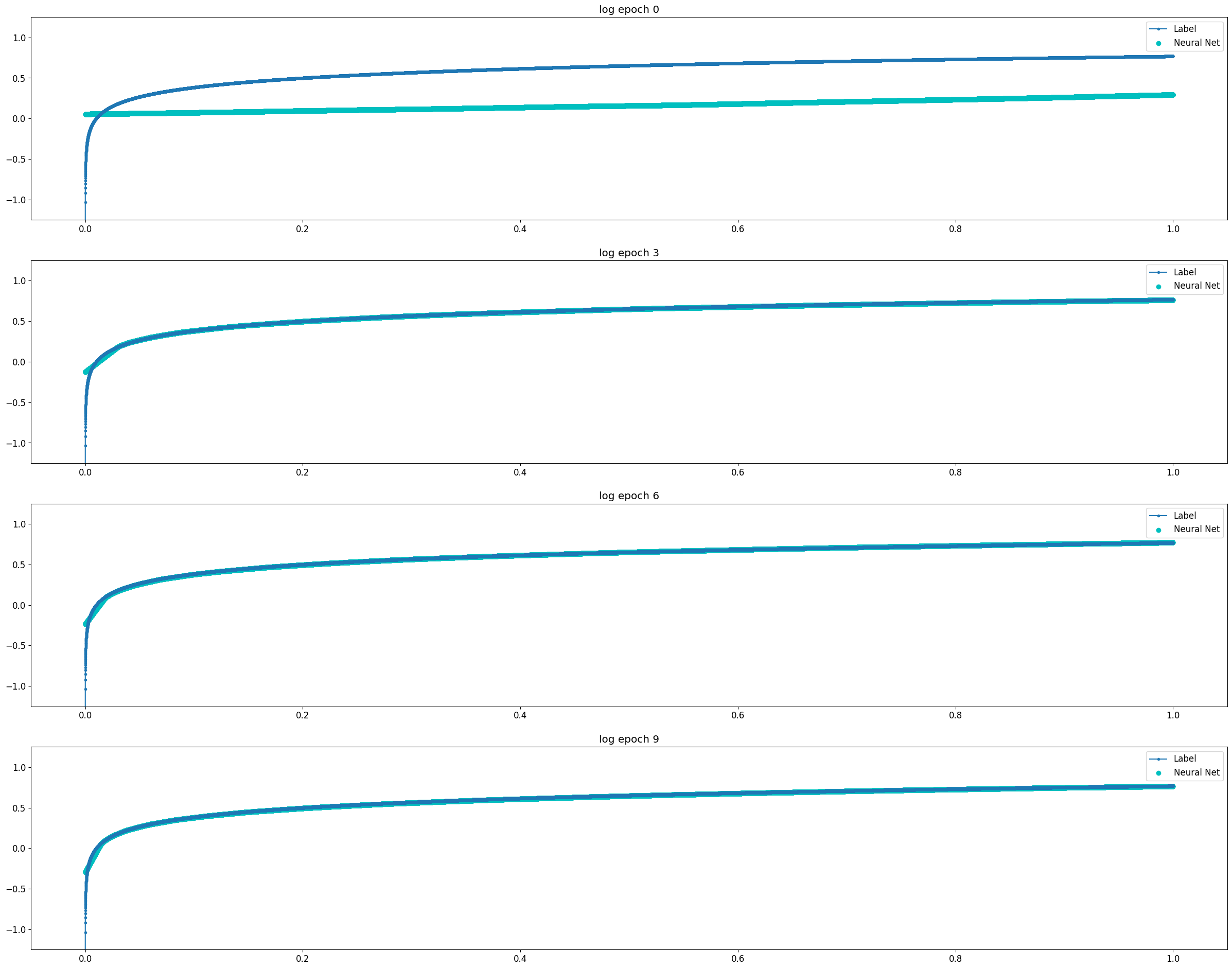
Polynomial Function
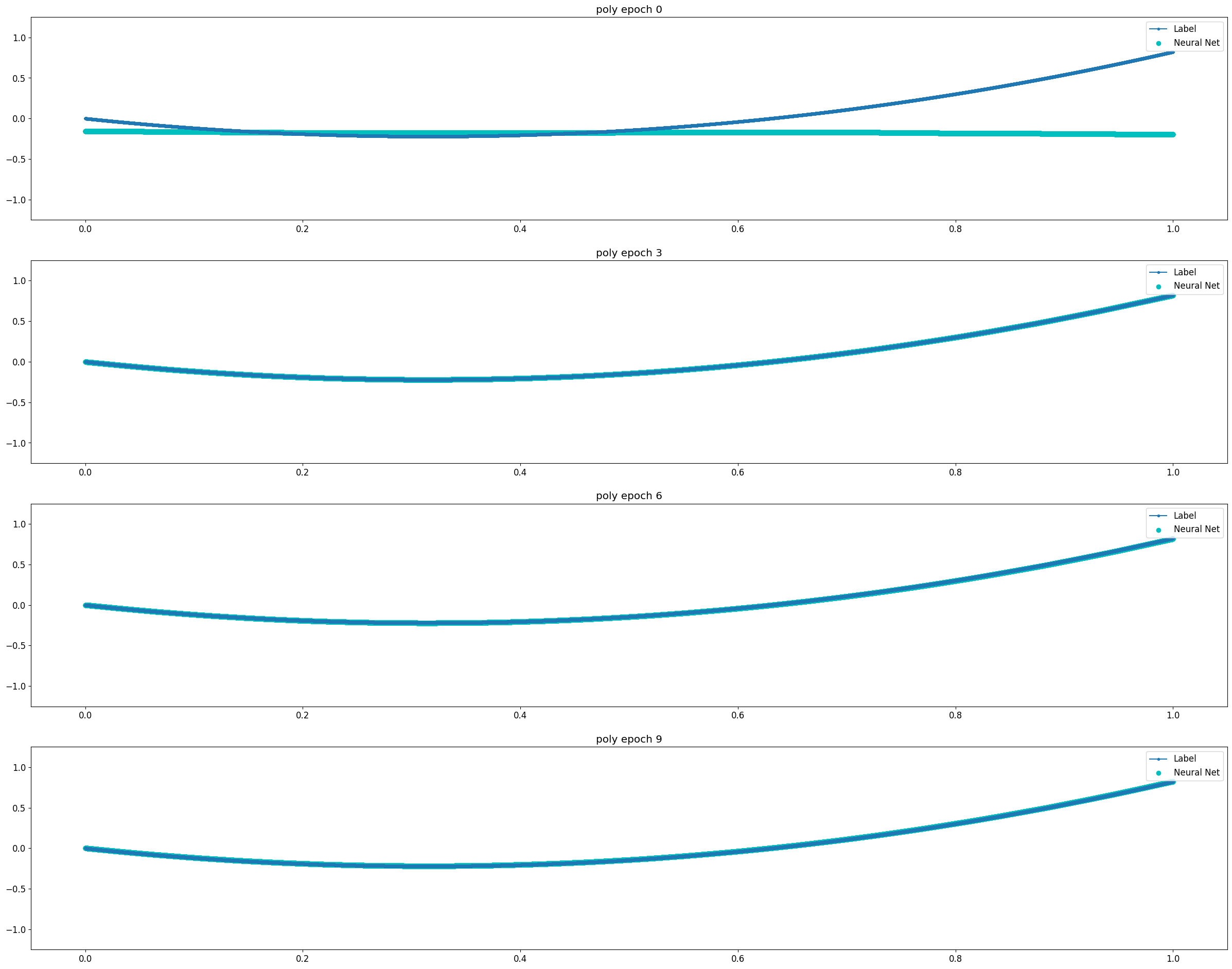
Sin Function
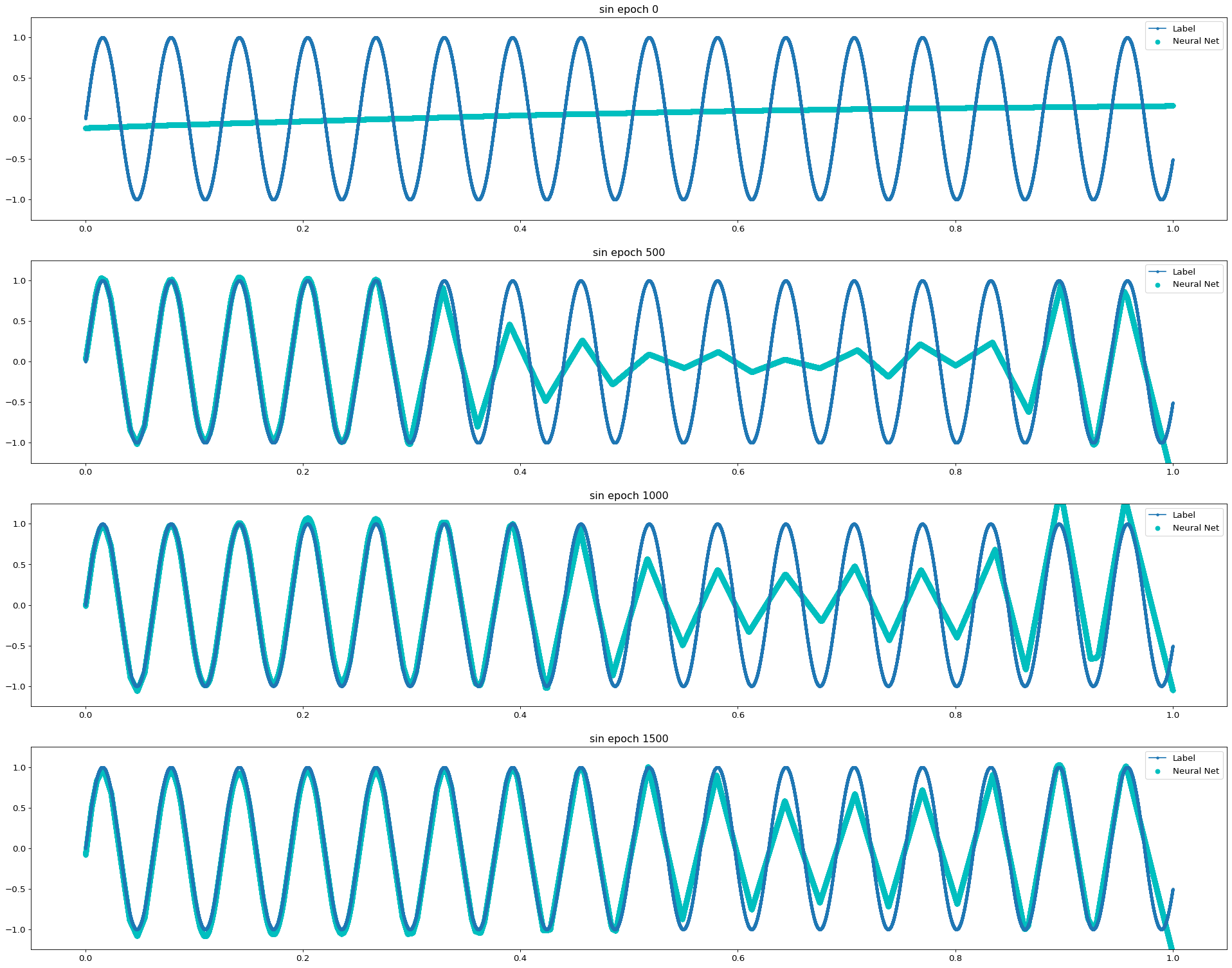
Discrete Function
Experiment 2) 3 Layer Model
Log Function

Polynomial Function
Sin Function
Discrete Function