Energy Based Model

• Yann LeCun의 A Tutorial on Energy-Based Learning과 Energy-based Approaches to Representation Learning을 참고하여 작성했습니다.

Introduction

Yann LeCun의 A Tutorial on Energy-Based Learning은 다음과 같은 문장으로 시작한다.

• “Energy-Based Models (EBMs) capture dependencies between variables by associating a scalar energy to each configuration of the variables”

Energy Based Model은 변수들 간의 의존성을 포착하는 모델이며, 각 변수들의 조합 간의 의존성 정도를 스칼라 값으로 나타낸 것을 Energy라고 한다는 것이다. 가장 익숙한 통계적 모델링 방법인 Probabilistic Model은 조건부 확률 \(P(Y \lvert X)\) 즉, 입력 \(X\)가 주어졌을 때 출력 \(Y\)가 나올 확률을 모델링한다면 Energy Based Model은 입력 \(X\)와 출력 \(Y\)의 조합을 통해 얻을 수 있는 Energy \(E(X, Y)\)의 값을 모델링한다. 정확하게 따지고 들어가면 LeCun도 강의에서

• “Probabilistic models are a special case of EBM”

라고 언급하듯 Probabilistic Model과 Energy Based Model은 완전히 별개의 방법이 아니며, 통계적 모델링에 대한 관점의 차이라고 할 수 있다. 하지만 이러한 관점의 차이로 보다 유연한 모델링이 가능하다고 한다.

Energy Function \(E(X, Y)\)

Energy Based Model에서는 Energy가 가장 낮은 \((X, Y)\)조합을 가장 정답에 가까운 것으로 본다.

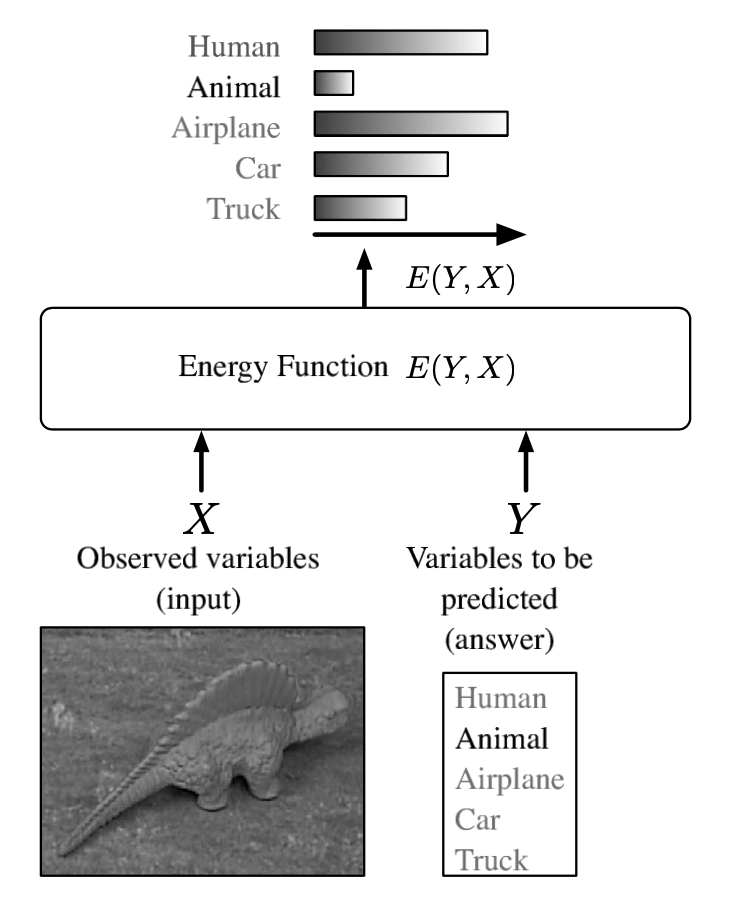
위의 그림을 보면 이구아나의 사진을 입력 \(X\)로 받고, 이를 5개의 레이블 Human, Animal Airplane, Car, Truck과의 Energy \(E(Y, X)\)를 각각 계산한 결과를 보여주고 있다. Energy Based Model에서는 Energy를 최소화하는 변수 조합을 찾는 것이 목표이므로 이구아나 사진에 대한 최적의 \(Y\) 변수 조합은 Animal이라는 것을 알 수 있다.

The smaller the better

이러한 점에서 Energy Function \(E(\cdot)\)은 변수 조합의 적절성(Compatibility)을 평가하는 함수로, 그 값이 작으면 작을수록 적절하다는 것을 의미한다. 이를 수식으로 표현하면 다음과 같다.

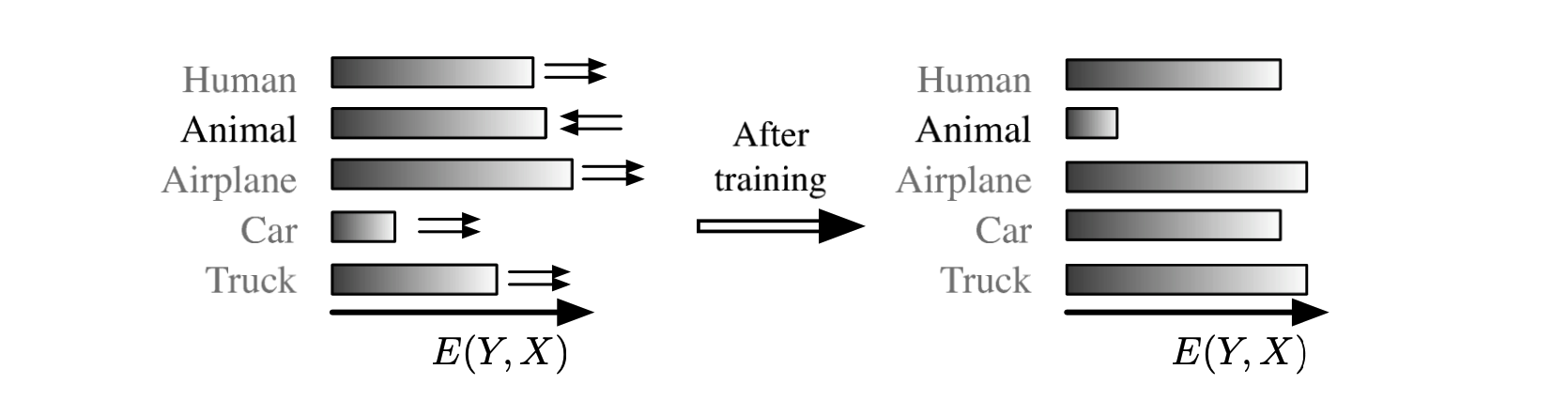
\[Y^* = \arg \min_{Y \in \mathcal y} E(X, Y)\]

이와 같이 Inference 시에 가능한 모든 조합에 있어 가장 Energy가 작은 것을 찾게 되므로 학습과 그에 맞는 손실 함수 또한 이에 맞춰 적용된다. 즉 학습의 경우 옳은 \((X,Y)\) 조합에 대해서는 낮은 Energy를, 틀린 \((X,Y)\) 조합에 대해서는 높은 Energy를 부여하는 Energy Function을 찾는 방향으로 이뤄지게 되고, 손실함수는 현재의 Energy Function이 각 조합에 대해 얼마나 Energy를 잘 부여하고 있는지 측정하는 역할을 하도록 설정하게 된다.

물론 변수가 연속적인 경우와 같이 가능한 \((X, Y)\) 조합의 개수가 너무 많아 각 조합의 Energy를 계산하는 것이 불가능한 경우도 많다. 이러한 경우 Global Minimum을 근사하도록 할 수 있는데, 대표적인 방법이 Gradient-Based Optimization Algorithm이다. 참고로 Gradient-Based Optimization Algorithm는 \(\mathcal y\)가 연속적이고 \(E(X,Y)\)가 smooth한 경우에만 적용이 가능하다.

Energy Based Model to Probabilistic Model

Introduction에서 언급한대로 Probabilistic Model은 Energy Based Model의 특수한 형태이다. 따라서 Energy Based Model을 Probabilistic Model의 형태로 표현할 수도 있는데, 가장 대표적인 것이 다음과 같은 Gibbs Distribution을 적용하는 것이다.

\[P(Y \lvert X) = {e^{- \beta E(Y, X)} \over {\int_{y \in \mathcal y} e^{-\beta E(y, X)}}}\]

여기서 \(\beta\)는 Inverse Temperature(\({1 \over kT}\))와 유사한 역할을 하는 양의 상수이고, 분모 \({\int_{y \in \mathcal y} e^{-\beta E(y, X)}}\)는 Partition Function이다. 현실적으로 이 Partition Function이 Intractable하게 주어지는 경우가 많으며 이는 곧 Probabilistic Model을 적용하는 데 있어 걸림돌이 된다.

Gibbs Distribution과 Probabilistic Model의 관계를 조금 더 명확히 하기 위해 \(E = -\log P\)를 가정하면 다음과 같아진다는 것을 알 수 있다.

\[P(Y \lvert X) = { \beta P(Y, X) \over \int_{y \in \mathcal y} \beta P(y, X) }\]

여기서 \(\beta = 1\)을 가정하면

\[P(Y \lvert X) = {P(Y, X) \over \int_{y \in \mathcal y} P(y, X) } = {P(Y, X) \over P(X)} = {P(X \lvert Y) P(Y) \over P(X)}\]

와 같이 베이즈 법칙의 꼴로 정리할 수 있다.

Energy Based Model as Implicit Function

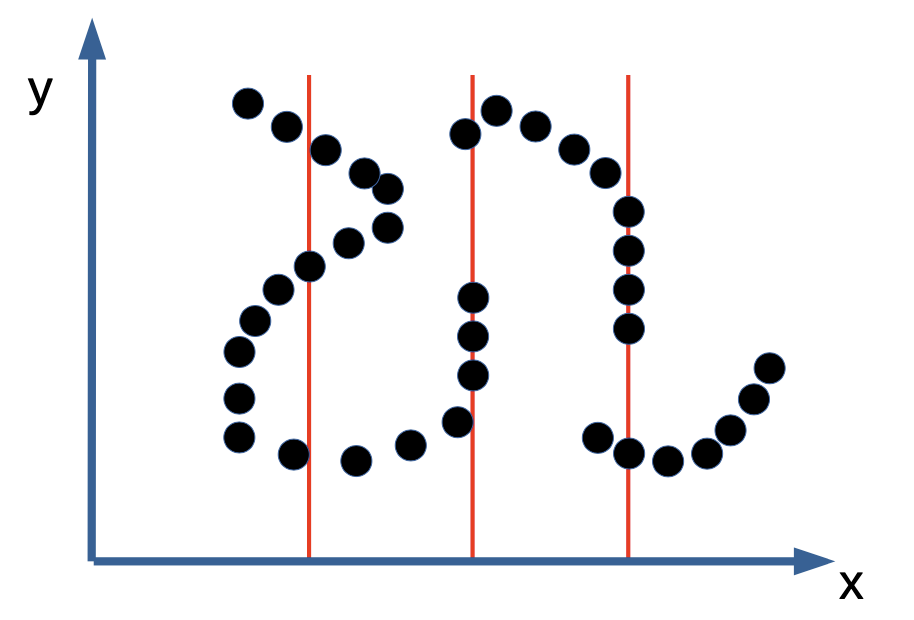
Explicit Function인 \(P(Y \lvert X)\)을 다루는 Probabilistic Model와 달리 \(E(X, Y)\)처럼 Implicit Function을 학습하는 Energy Based Model은 아래 이미지와 같이 하나의 \(X\)에 대해 여러 개의 \(Y\)가 가능한 경우에 효과적이다.

Loss Functions for Energy Based Model

그렇다면 Energy Based Model은 어떻게 학습이 이뤄질까. Energy Based Model을 학습한다는 것은 최적의 Energy Function을 찾는 것이라고 할 수 있다. 이때 가능한 모든 Energy Function의 집합을 \(\mathcal E\)라고 하자.

\[\mathcal E = \{ E(W,Y,X): W \in \mathcal W \}\]

데이터셋이 \(S = \{ (X^i, Y^i):i=1...P \}\) 로 주어져있고, 이에 대해 Energy Function이 얼마나 좋은지 평가하는 Loss Functional \(\mathcal L (W, S)\)가 있다면, Energy Function의 최적 파라미터 \(W^*\)는 다음과 같이 Loss의 크기가 가장 작은 경우로 정의할 수 있다.

\[W^* = \min_{W \in \mathcal W} \mathcal L (W, S)\]

다른 모델들과 마찬가지로 Loss Functional \(\mathcal L (W, S)\)을 어떻게 설정하느냐에 따라 Energy Based Model의 적절한 파라미터 \(W\)를 찾을 수 있기 때문에 Loss Function을 결정하는 문제는 매우 중요하다.

Designing a Loss Function

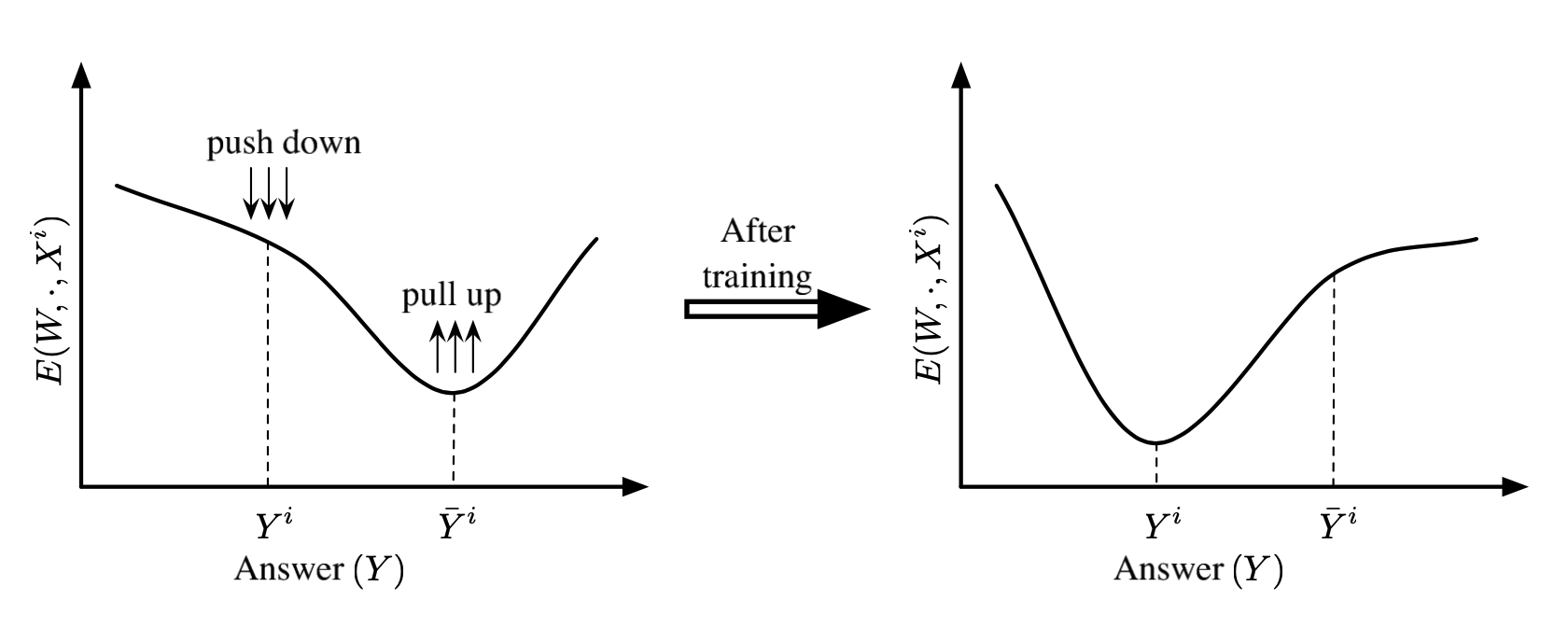
좋은 Energy Function이란 앞서 여러 번 언급한 대로 최적의 조합에 대해서는 낮은 Energy를, 이외의 조합에 대해서는 높은 Energy를 부여하는 것으로 이해할 수 있으며, 이를 잘하면 잘할수록 Loss Function으로 구해지는 Loss의 크기가 줄어들어야 한다. 학습의 관점에서 말하면 Loss Function을 통해 학습을 진행하여 옳은 조합에 대해서는 Energy를 낮추고(Push Down), 이외의 조합에 대해서는 Energy를 높이도록(Pull Up) 할 수 있어야 한다. Tutorial에서는 다음과 같은 Notation을 사용하여 여러 종류의 Loss Function을 제시하고 있다.

• \(E\): Energy Function
• \(Y^i\): Correct Answer
• \(Y^{*i}\): The Answer Produced By the Model
• \(\bar Y^i\): The Answer that has the Lowest Energy among all the Incorrect Answers

예를 들어 \(E(W, Y^i, X^i)\)는 옳은 조합이므로 낮춰야 하고, \(E(W, \bar Y^i, X^i)\)는 틀린 조합이므로 높여야 한다.

Energy Loss

Energy Loss는 다음과 같이 정답 Label \(Y^i\)로 구해지는 Energy 값을 Loss로 하는 방법을 말한다.

\[L(Y^i, E(W, \mathcal y, X^i)) = E(W, Y^i, X^i)\]

매우 간단하면서도 정답 \(E(W, Y^i, X^i)\)의 Energy를 낮추는 방향으로 학습을 진행하도록 하는 방법이다. 하지만 이 경우 오답 Energy는 증가할 수 없고, 항상 Energy의 크기가 작아지기만 하기 때문에 Collapsed Solution을 만들어낼 수 있다는 단점을 가지고 있다. Energy Loss의 가장 대표적인 예는 다음과 같이 L2 Norm을 사용하는 것이다.

\[E(W, Y^i, X^i) = \| Y^i - G(W, X^i) \|^2\]

Generalized Perceptron Loss

오답의 Energy가 증가하지 않는다는 Energy Loss의 문제점을 해결하기 위해 \(\min_{y \in \mathcal y} E(W, Y, X^i)\) Term을 추가한 방법이다.

\[L(Y^i, E(W, \mathcal y, X^i)) = E(W, Y^i, X^i) - \min_{y \in \mathcal y} E(W, Y, X^i)\]

이를 사용하면 \(E(W, Y^i, X^i)\)의 Energy는 작아지는 동시에 그 이외의 조합에 대해서는 Energy가 커지도록 할 수 있다.

Negative Log-Likelihood Loss

Maximum Conditional Probability Principle에 따르면 데이터셋 \(S = \{ (X^i, Y^i):i=1...P \}\)가 주어져 있을 때 모델의 파라미터 \(W\)는 다음 식을 극대화하는 방향으로 업데이트되어야 한다.

\[P(Y^1, ... Y^P \lvert X^1, ... X^P, W) = \Pi_{i=1}^P P(Y^i \lvert X^i, W)\]

이때 양변에 \(-\log\)를 씌워주면 익숙한 Negative Log-Likelihood 식을 구할 수 있다.

\[- \log \Pi_{i=1}^P P(Y^i \lvert X^i, W) = \Sigma_{i=1}^P - \log P(Y^i \lvert X^i, W)\]

앞서 확인한 Gibbs Distribution으로 \(P(Y^i \lvert X^i, W)\)를 대체하게 되면 다음과 같은 식을 구할 수 있다.

\[\eqalign{ - \log \Pi_{i=1}^P P(Y^i \lvert X^i, W) &= \Sigma_{i=1}^P - \log P(Y^i \lvert X^i, W) \\ &= \Sigma_{i=1}^P \beta E(W, Y^i, X^i) + \log \int_{y \in \mathcal y} e^{-\beta E (W, \mathcal y, X^i)} }\]

따라서 Negative Log-Likelihood Loss는 다음과 같이 정의된다. 위의 식에서 \({1 \over P \beta}\)를 곱해준 것이다.

\[\eqalign{ L(Y^i, E(W, \mathcal y, X^i)) &= E(W, Y^i, X^i) + \mathcal F_\beta (W, \mathcal y, X^i) \\ \mathcal F_\beta (W, \mathcal y, X^i) &= {1 \over \beta} \log (\int_{y \in \mathcal y} \exp (-\beta E(W, y, X^i))) }\]

Negative Log-Likelihood Loss를 Energy Based Model의 관점에서 볼 때 한 가지 재미있는 점은 Gradient를 통해 확인할 수 있다.

\[{\partial L(Y^i, Y^i, X^i) \over \partial W} = {\partial E(W, Y^i, X^i) \over \partial W } - \int_{Y \in \mathcal y} {\partial E(W, Y, X^i) \over \partial W} P(Y \lvert X^i, W)\]

즉 Contrastrative Term의 Gradient \(- \int_{Y \in \mathcal y} {\partial E(W, Y, X^i) \over \partial W} P(Y \lvert X^i, W)\) 으로 인해 모든 \(Y\)에 대해 Energy가 커지게 된다는 점이다. 이때 각 \(Y\)에 대해 커지는 크기는 Model에 따랐을 때의 Likelihood \(P(Y \lvert X^i, W)\)에 비례하게 된다. 물론 정답에 대해서는 \({\partial E(W, Y^i, X^i) \over \partial W }\) Term으로 Energy가 커지는 크기가 조정된다.

Analysis of Loss Functions for Energy-Based Models

위에서 확인한 Loss Function 중 가장 좋은 Loss Function이 무엇인지 시각적으로 확인하는 방법으로 Energy Surface가 있다. 이름에서 유추할 수 있듯 Energy Surface는 입력 \(X\)와 출력 \(Y\)의 평면 상에서 Energy의 크기를 나타낸 것인데, 데이터셋 \(S\)에 포함되어 있는 조합 \((Y^i, X^i)\)와 그 주변은 상대적으로 Energy가 낮고, 이외의 경우에 대해서는 Energy가 높은 형태일수록 좋은 Energy Surface이다. 이는 보다 좋은 Loss Function으로 학습한 결과라고도 할 수 있다.

• “The Energy Surface is a “contrast function” that takes low values on the data manifold, and higher values everywhere else”

각각의 Loss Function에 대해 Energe Surface를 확인해보면 다음과 같다.

Energy Loss

실험에 사용한 Energy Loss Function은 Robust Regression과 같이 L1 Norm을 사용했다.

\[L(W, S) = {1 \over P} \Sigma_{i=1}^P \| G_W(X) - Y \|^1\]

아래 그림을 보게 되면 a에서 d로 학습이 진행됨에 따라 검은색 데이터 포인트 주변의 Energy는 줄어들고 그 이외의 영역에 대해서는 Energy가 커지는 것을 확인할 수 있다.

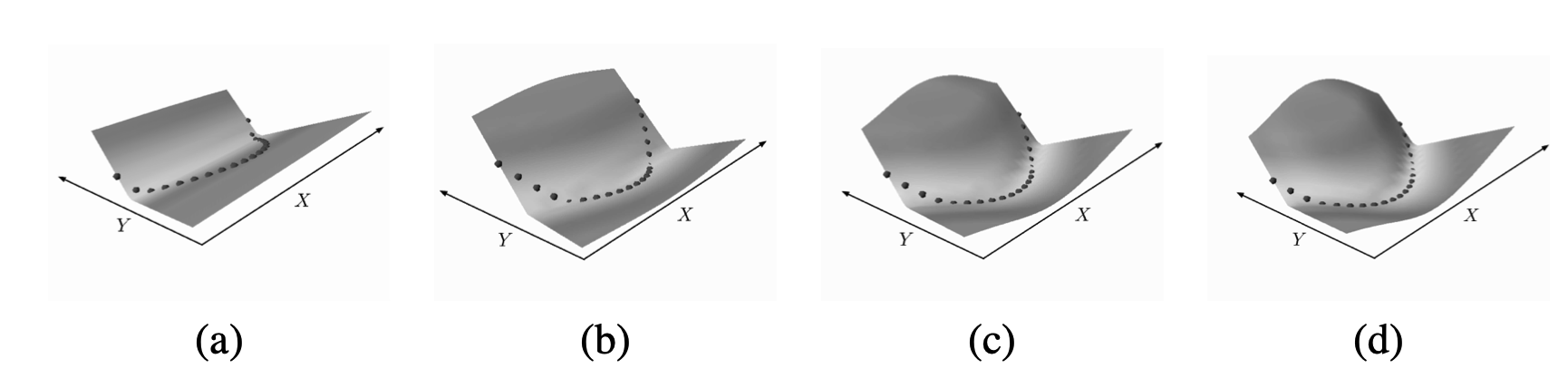
Energy Loss with Implicit Regression

전체적인 구조는 위의 Energy Loss와 동일하나, \(X\) 뿐만 아니라 \(Y\)도 네트워크를 통과시킨 후 얻은 값으로 Loss를 구하는 방법이다.

\[L(W, S) = {1 \over P} \Sigma_{i=1}^P \| G_{W_1}(X) - G_{W_2}(Y) \|^1\]

이 경우 아래 그림처럼 데이터 포인트와 무관하게 모든 영역의 Energy가 동일함을 알 수 있다. 이는 Input과 무관하게 Energy Loss를 항상 최소화시키는 방향으로 \(W_1, W_2\)가 업데이트 되기 때문이다.

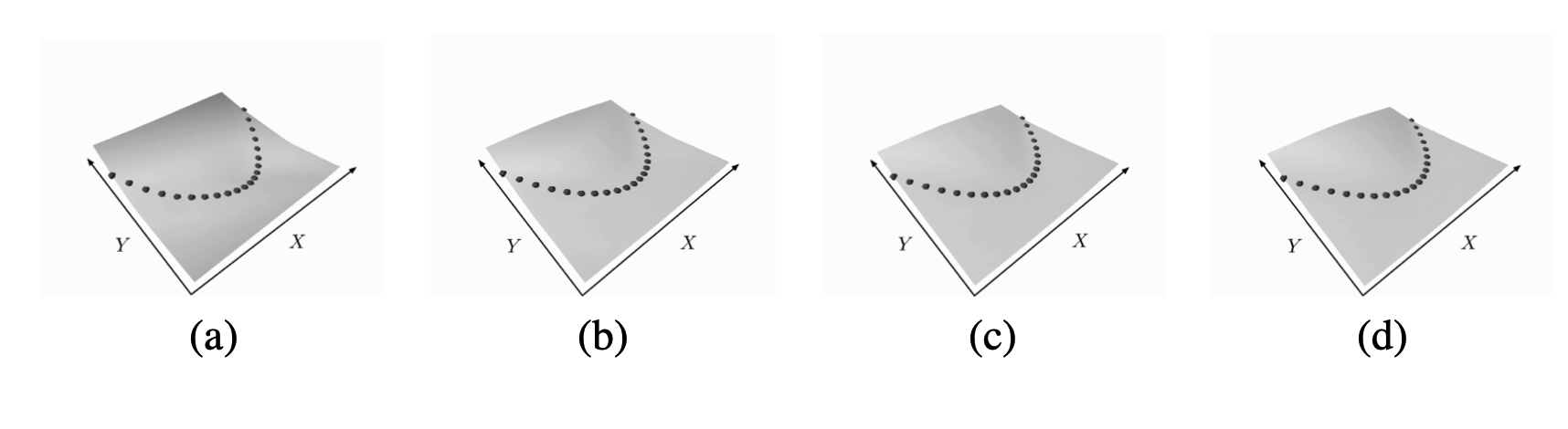
Square-Square Loss

Square-Square Loss는 다음 식을 통해 구해진다.

\[L(W, Y^i, X^i) = E(W, Y^i, X^i)^2 - (\max(0, m-E(W, \bar Y^i, X^i)))^2\]

두 번째 Term으로 인해 정답 이외의 조합이 가지는 Energy가 일정 수준(\(m > 0\)) 이하로 떨어지지 않도록 하는 방법이라고 할 수 있다. 이로 인해 Energy Surface도 원하는 대로 나오게 된다.

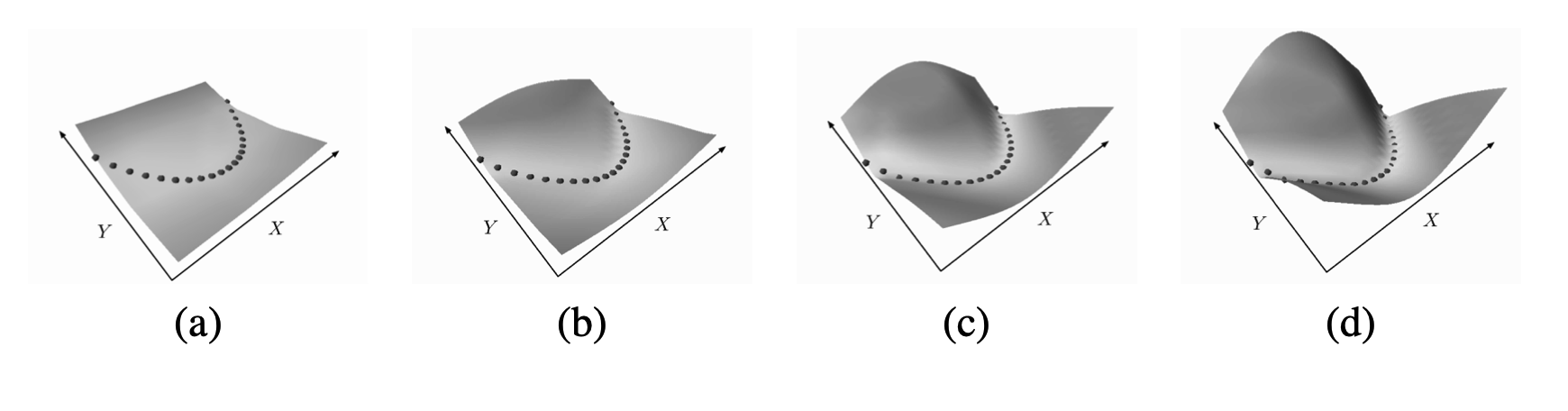
Negative Log Likelihood Loss

앞서 확인한대로 Negative Log Likelihood Loss의 첫 번째 Term은 정답 조합 \((Y^i, X^i)\)에 대해 Energy를 낮추어주는 역할을, 두 번째 Term은 모든 \(y\)에 대해 Energy를 높여주는 역할을 한다.

\[L(Y^i, E(W, \mathcal y, X^i)) = E(W, Y^i, X^i) + {1 \over \beta} \log (\int_{y \in \mathcal y} \exp (-\beta E(W, y, X^i)))\]

Energy Surface는 아래처럼 극단적으로 나오는데, 이는 앞서 확인한 다른 방법들과는 달리 오답인 조합에 대해서는 Energy가 무한히 증가할 수 있기 때문이다.

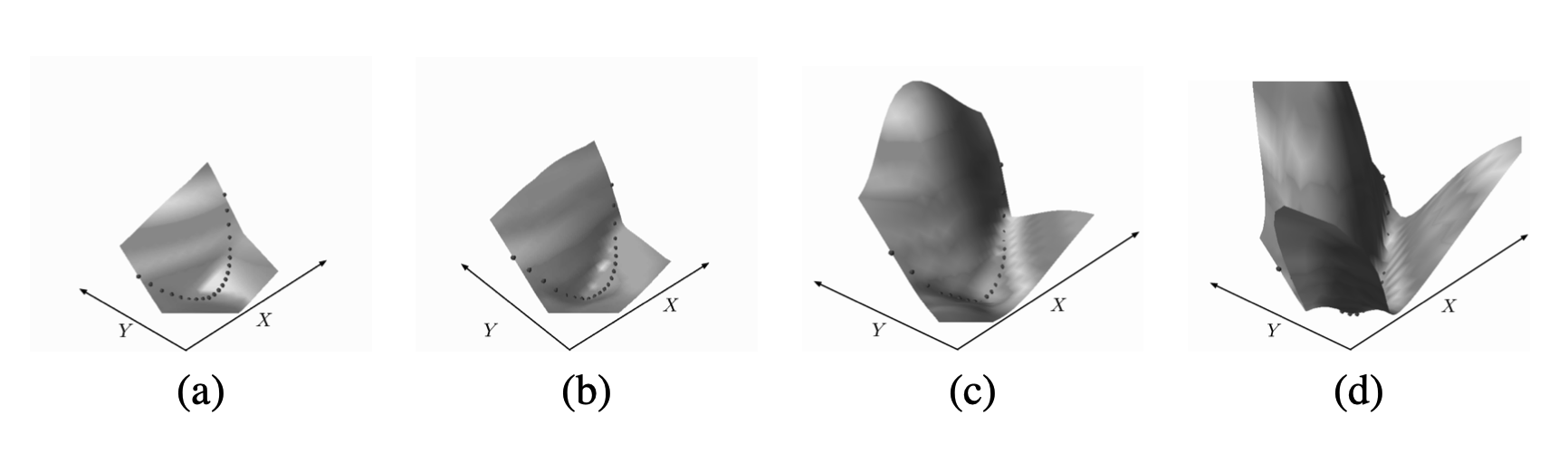
한 가지 특징이 있다면 정답인 경우에도 Energy가 0이 되지 않을 수도 있다는 것이다. 따라서 어떤 조합이 좋고 나쁨을 논할 때 Energy의 절대적인 크기로 비교해서는 안 되고, 전체 가능한 Answer들 중에서 얼마나 Energy가 낮은지를 확인해야 한다.