Convolution Neural Network

• Ian Goodfellow, Yoshua Bengio, Aaron Courville의 Deep Learning Book을 참고하여 작성했습니다.

CNN의 정의

Deep Learning Book에서는 CNN을 격자형 위상을 가진 데이터를 처리하는 데에 특화된 뉴럴 네트워크라고 정의하고 있다. 격자형 위상을 가진 대표적인 객체로 사진(이미지)가 있으며, 실제로 최근 사진 데이터를 다룰 때에는 목적과 상관없이 기본적으로 CNN을 사용한다.

Convolution operation

CNN에서 C는 Convolution이라는 수학 연산을 의미한다. 즉, CNN은 Convolution 연산을 사용하는 뉴럴 네트워크라고 할 수 있다. 기존에는 음파와 같은 신호 처리가 필요한 분야에서 noise의 영향을 줄이며 안정적인 신호를 탐지하는 방법으로 사용되어 왔는데, 구체적인 수식은 아래와 같다.

\[s(t) = \int_{-\infty}^{\infty} x(a)w(t-a)da\]

위의 식에서 \(x(t)\)는 현재 시점 \(t\)에 수신기를 통해 받은 신호의 크기를, \(w(h)\)는 어떤 시점 \(h\)에 부여되는 가중치를 각각 뜻한다. 이러한 의미를 감안할 때 convolution 식은 특정 시점 \(t\)의 값 \(s(t)\)를 구하기 위해 현재 시점의 값 뿐만 아니라 과거에 측정된 값들을 적절한 비율로 가중 평균하여 사용하는 것으로 이해할 수 있다.

적분 값이라 다소 추상적인데, 이산적인 상황을 가정하면 다음과 같이 표현된다. 실제로 컴퓨터는 이산적으로 동작한다는 점에서 아래의 수식이 보다 적합하다고도 할 수 있다.

\[s(t) = \Sigma_{a=-\infty}^{\infty} x(a) w(t-a)\]

이러한 convolution operation은 \(*\)로 표기한다. 즉 위의 식 \(s(t)\)는 \((x * w)(t)\)와 같다. 이때 먼저오는 피연산자를 input이라고 부르고, 다음에 오는 피연산자를 kernel이라고 한다. 그리고 출력값은 feature map이라고 한다.

convolution integral limits

convolution operation에서 무한의 범위에 대해 적분을 취하는 것에 대해 찾아보니 stack exchange에서는 기본 가정과 관련된다고 한다. 즉 convolution의 피연산자들은 모두 non-negative value만 가질 수 있어 함수의 값이 양수인 경우와 전체를 보는 경우의 적분값이 같아진다고 한다. 위의 수신기 예시에서도 수신기의 출력값은 감지된 신호가 없거나(0), 있는(\(\rm I\!R^+\)) 경우 밖에 없고, 가중치를 나타내는 \(w\) 또한 반영하지 않거나(0), 반영하는 크기(\(\rm I\!R^+\))로 두 경우로 모두 공역이 양의 실수 범위를 갖는다. 이러한 점에서 무한으로 범위를 표기한 것은 곱의 결과가 양수인 범위는 알 수 없으므로, 일반화를 위한 것으로 이해할 수 있다.

예를 들어 함수 \(g\)의 값이 양수인 범위가 0부터 2라면 \((f*g)(t)\)는 다음과 같이 표현할 수 있다.

\[(f*g)(t) = \Sigma_{a=2}^{0} f(a) g(t-a)\]

이를 뉴럴넷에 적용하여 사진 등의 특징을 추출하는 방법으로 사용하는 것이다.

2D convolution operation

위에서는 신호 처리에 사용되는 convolution operator를 보았는데, 이 경우 시간축 \(t\)만 존재했으므로 1차원 공간이라고 할 수 있다. 비슷한 방법으로 이미지와 같은 2차원 공간에서도 convolution operation을 적용할 수 있는데, input이 2차원이 되었으므로 kernel 또한 2차원이 된다.

\[S(i,j) = (I*K)(i,j) = \Sigma_m \Sigma_n I(m,n) K(i-m, j-n)\]

그런데 convolution operation은 교환법칙이 성립한다.

\[S(i,j) = (K*I)(i,j) = \Sigma_m \Sigma_n I(i-m, j-n) K(m, n)\]

논리적으로는 위의 첫 번째 식이 맞지만, 머신러닝에서 이미지 등을 처리할 때에는 m, n의 변동이 적기 때문에 아래의 식을 주로 이용한다고 한다. 위의 식을 그대로 이용하여 convolution network를 구성하면 입력으로 주어진 이미지의 pixel index가 늘어날 때마다 곱해지는 kernel의 index는 줄어들게 된다. 즉, kernel이 뒤집혀진(flipped) 채로 곱해지는 것이다. 구현의 편의를 위해 뒤집지 않고 각 element를 그대로 곱해도 되는데, 이를 cross-correlation 이라고 한다. 실제로 많은 머신러닝 라이브러리에서는 kernel을 뒤집지않고 아래 cross-correlation 식을 이용하여 convolution network를 구현하고 있다.

\[S(i,j) = (K*I)(i,j) = \Sigma_m \Sigma_n I(i+m, j+n) K(m, n)\]

Convolution and Matrix multiplication

이산의 convolution 연산은 행렬 간의 곱으로 표현할 수 있다. 하지만 이때 곱해지는 행렬의 경우 몇 가지 조건이 붙는다. 구체적으로 1차원 convolution 연산의 경우 행렬은 각 row가 한 칸씩 수평이동한 형태, 즉 Toeplitz matrix의 특성을 갖는다. 2차원에서는 doubly block circulant matrix로, 많은 element가 0으로 구성되는 sparse matrix의 특성을 갖는다. 이는 kernel이 image 전체의 크기에 비해 매우 작다는 점을 고려하면 당연하다.

\[\eqalign{ \begin{bmatrix} x_1 && x_2 && x_3 \\ x_4 && x_5 && x_6 \\ x_7 && x_8 && x_9 \\ \end{bmatrix} &* \begin{bmatrix} k_1 && k_2 \\ k_3 && k_4 \\ \end{bmatrix}\\ &= \begin{bmatrix} k_1 && k_2 && 0 && k_3 && k_4 && 0 && 0 && 0 && 0 \\ 0 && k_1 && k_2 && 0 && k_3 && k_4 && 0 && 0 && 0 \\ 0 && 0 && 0 && k_1 && k_2 && 0 && k_3 && k_4 && 0\\ 0 && 0 && 0 && 0 && k_1 && k_2 && 0 && k_3 && k_4 \\ \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ x_8 \\ x_9 \\ \end{bmatrix} }\]

CNN의 세 가지 특성

convolution operation을 뉴럴 네트워크에 적용한 CNN은 sparse interaction, parameter sharing, equivariance to translation이라는 세 가지 특성을 갖는다.

1. Sparse interaction

Sparce interaction란 convolution layer의 각 출력값이 layer의 전체 입력값이 아닌 매우 작은 일부분에 의해 결정된다는 특성을 말한다. 이는 전체 image에 비해 매우 작은 kernel의 크기로 쉽게 떠올릴 수 있다. 이러한 점은 저장해야 할 네트워크의 크기 감소와 연산량 자체의 감소로 이뤄져 효율적인 연산을 가능하게 한다.

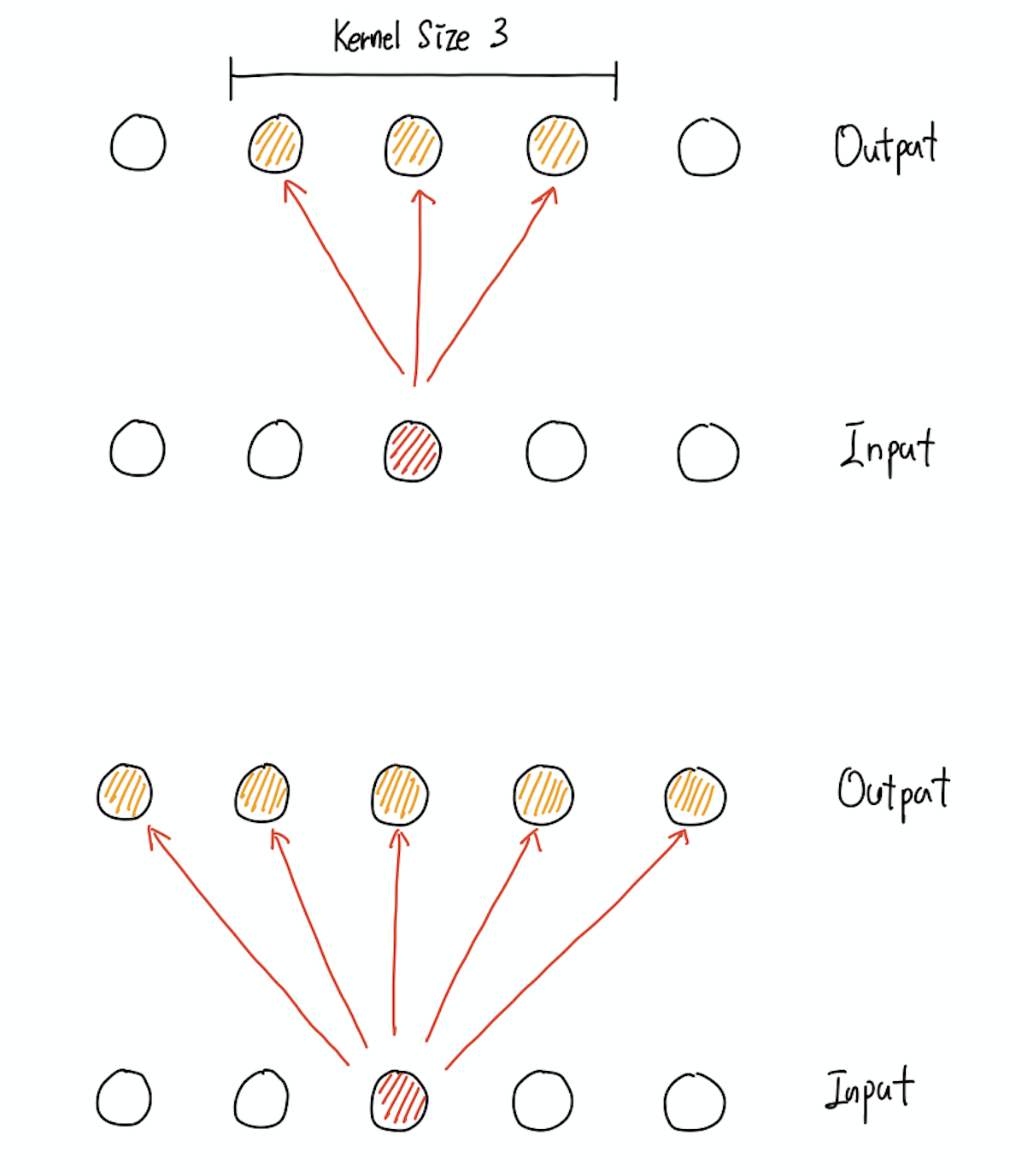
그림을 통해 보면 보다 명확한데, 위의 그림에서 첫 번째 그림이 Kernel size가 3인 convolution layer를 표현한 것이고, 두 번째 그림이 일반적인 Fully Connected layer를 표현한 것이다 convolution layer의 경우 입력층의 하나의 값이 세 개의 출력층 값에만 영향을 미치지만, Fully Connected layer의 경우 입력층 하나의 값이 모든 출력층 값에 영향을 미치는 것을 확인할 수 있다. 이러한 점에서 Sparse하다고 말하는 것이다.

2. Parameter Sharing

Sparse interaction이 입력값과 출력값의 관점에 집중한 특성이라면 Parameter Sharing은 kernel과 관련된다. Fully Connected layer에서는 layer를 구성하는 각 element는 전체 출력에 단 한 번만 사용된다. 반면 Convolution layer에서는 kernel의 사이즈는 작지만 kernel을 구성하는 각 element는 layer의 모든 개별 출력값에 중복적으로 사용된다.

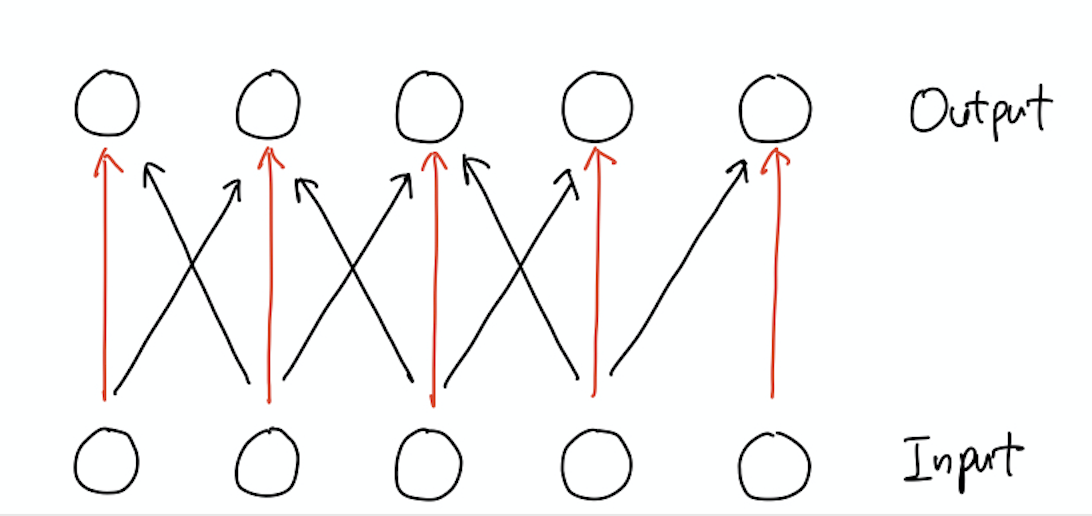
보다 구체적으로 위와 같이 Kernel size가 3인 convolution layer에서 빨간 색으로 표현된 edge의 값은 모두 동일하다. 정확하게는 kernel이 좌우로 이동하며 계산하기 때문에 공유되는 값이다. 이러한 점에서 sharing이라는 표현을 사용한다.

3. Equivariance to translation

어떤 함수가 equivariant 하다는 것은 입력이 변화하면 그에 맞춰 출력도 변화한다는 것을 의미한다. 수학적으로는 다음과 같은 공식이 성립할 때 함수 \(f(x)\)는 \(g\)와 equivariant하다고 말한다.

\[f(g(x)) = g(f(x))\]

이때 함수 \(f\)를 어떤 이미지 \(x\)에 대해 특정한 값을 출력하는 Convolution Layer이고, \(g\)가 어떤 이미지에 대해 적절한 변형을 가하는 함수라고 한다면 이러한 특성이 무엇을 의미하는지 보다 이해하기 쉬워진다. 즉 이미지에 변형을 가한 후 Convolution를 수행하는 것이나, Convolution을 수행한 후 동일한 변형을 출력값에 가한 것이나 동일하다는 것이다. 여기서 말하는 적절한 변형이란 회전(rotation), 스케일 조정(scale), 전단(shear), 이동)(shift) 등을 포함한다.

equivariance and invariance

CNN을 사용한 논문을 읽다보면 equivariance라는 표현과 함께 invariance라는 표현이 자주 등장한다. 의미적으로는 equivariance와 invariance는 거의 차이가 없지만 정확하게는 영어 접두사적 표현에 차이가 있다고 한다. stack exchange에 따르면 접두사 in-은 no의 의미를 가지고 equi-는 varying in a similar or equivalent proportion 정도의 의미를 가진다고 한다. 정리하면 invariance는 변화가 전혀 없다는 것을, equivariance는 약간의 변화가 있을 수 있지만 거의 같다는 것으로 볼 수 있다.