Loss function과 Maximum likelihood

Introduction

딥러닝은 gradient descent 방법을 이용하여 최적의 모델을 찾는다. 즉 딥러닝 모델을 어떤 함수 \(f_\theta(\cdot)\)라고 할 때 학습과정에서 이 함수가 가지는 파라미터 \(\theta\)는 loss function \(L(\cdot)\)을 최소화하는 방향으로 변화하며, 이때 loss를 최소화하는 변화의 방향과 크기를 loss function의 미분값인 gradient를 이용해 결정한다. 그리고 이 gradient를 back propagation 방법을 통해 업데이트하는 것이 기본적인 딥러닝의 개념이다.

\[\theta^* = argmin_{\theta \in \Theta} L(f_\theta(x), y)\]

이러한 점에서 loss function을 어떻게 설정할지에 관한 문제는 딥러닝에서 매우 중요하다고 할 수 있다. 하지만 딥러닝에서 사용되는 loss function의 종류는 매우 제한적인데, 이를 Maximum likelihood의 관점에서 풀어보고자 한다.

likelihood

위키피디아에서는 likelihood를 다음과 같이 정의하고 있다.

• “확률변수 \(X\)가 모수 \(\theta\)에 대한 확률분포 \(P_\theta(X)\)를 가지며, \(X\)가 특정한 값 \(x\)로 표집되었을 경우, \(\theta\)의 likelihoode function은 다음과 같이 정의된다.”

\[L(\theta | x) = Pr(X = x | \theta)\]

쉽게 말하면 어떤 확률분포의 모수를 \(\theta\)라고 했을 때, 표본 \(x\)가 그럴듯한 정도를 의미한다. 따라서 \(\theta\)가 실제 모수와 비슷하다면 likelihood 또한 높아지게 된다.

참고로 여기서 말하는 모수란 모집단의 특성을 설명하는 통계량이라고 할 수 있으며, 대표적인 모수로는 정규분포의 평균과 표준편차가 있다. 모수의 대상은 모집단이므로 상수이지만 정확한 수를 알 수가 없기 때문에 일반적으로 \(\mu, \sigma\)와 같은 그리스 문자로 표현한다.

모수를 안다는 것은 모집단의 특성을 안다는 것을 의미하므로, 표본을 통해 모수를 추정하는 방법이 사용되는데 이를 모수 추정(parameter estimation)이라고 한다.

Maximum likelihood

그렇다면 likelihood 개념과 딥러닝은 어떤 관계가 있을까. 이활석 님의 오토인코더의 모든 것에서 이에 관해 잘 설명해주고 있는데 요약하자면 다음과 같다.

어떤 네트워크 \(f_\theta(\cdot)\)이 있고, 데이터셋에는 네트워크 입력값 \(x = \{ x_1, x_2, ... x_n \}\)와 이에 대한 레이블 \(y = \{ y_1, y_2, ... y_n \}\) 이 저장되어 있다고 하자. 입력값 \(x\)를 네트워크에 넣은 출력값은 \(f_\theta(x)\), 우리가 가지고 있는 정보라고 할 수 있다. 이 정보를 이용해 y를 예측하는 것이 네트워크의 목표가 된다. 확률적으로 표현하면 조건부 확률분포 \(p(y \lvert f_\theta(x))\)를 높이는 방향으로 네트워크가 업데이트 되어야 한다.

이때 \(p(y \lvert f_\theta(x))\)이 정규분포를 따른다고 가정하면, \(f_\theta(x)\)는 정규분포의 모수, 즉 평균(표준편차는 편의상 생략)으로 볼 수 있다. 이렇게 보면 네트워크의 출력값은 미리 가정한 확률분포의 모수를 추정하는 것이 된다.

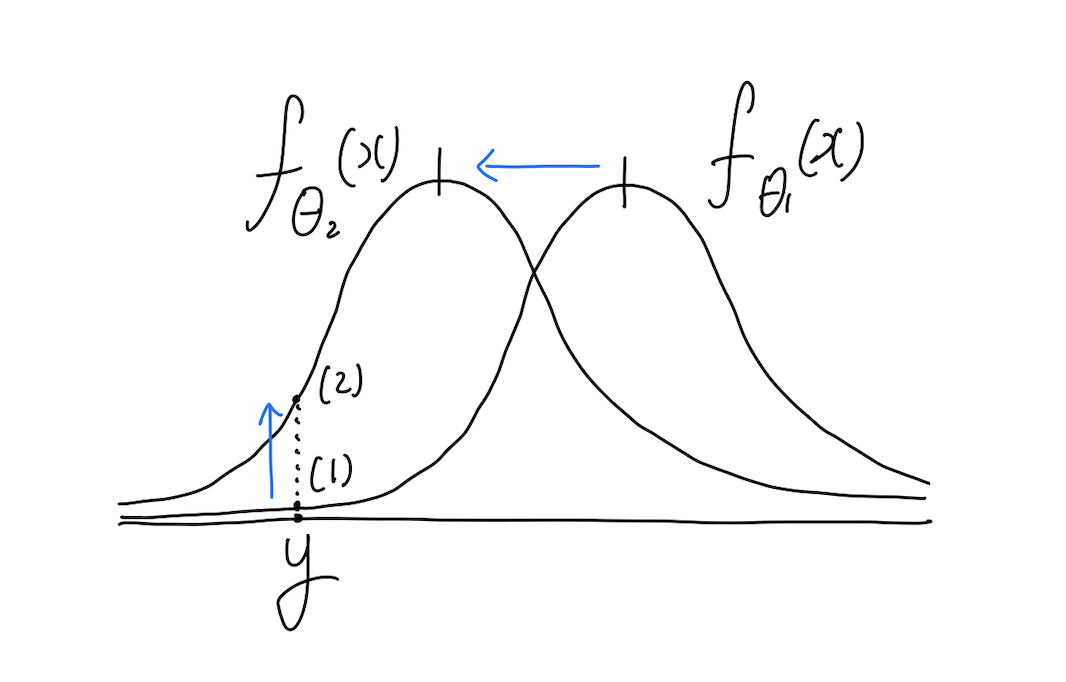
위의 그림을 보면 조금 더 쉽게 이해가 되는데, 네트워크 학습 과정에서 \(\theta_1\)이 \(\theta_2\)로 변화했다고 하자. 네트워크의 출력값을 확률분포 \(p(y \lvert f_\theta(x))\)의 평균값으로 보기 때문에 위의 그림과 같이 정규분포의 형태로 표현할 수 있다. 즉 네트워크 출력값이 변화하여 평균이 \(f_{\theta_1}(x)\)에서 \(f_{\theta_2}(x)\)로 이동한 것이다. 이때 각 네트워크의 성능은 결국 해당 확률분포에서 y값의 likelihood, 그림 상의 (1)과 (2)로 표현된다. y가 나올 확률을 최대로 하는 것이 목표이므로 (1)보다는 (2)가 좋은 것이다.

이러한 관점에서 보게 되면 딥러닝 모델을 학습시키는 문제는 likelihood 값을 극대화하는 문제, 즉 maximum likelihood 문제가 된다.

maximum likelihood and loss function

위와 같이 maximim likelihood 관점에서 보면 \(p(y \lvert f_\theta(x))\)를 극대화하는 \(\theta\)를 찾는 것이 딥러닝 모델의 목표다.

\[\theta^* = argmin_\theta \ p(y \lvert f_\theta(x))\]

그렇다면 loss를 다음과 같이 표현할 수 있다. \(y\)의 likelihood 값에 반비례하게 loss를 설정하기 위해 마이너스를 붙였다.

\[loss : -p(y \lvert f_\theta(x))\]

그런데 이 경우 likelihood의 계산이 복잡하다. 따라서 일반적으로 log를 취하는 Log likelihood를 사용한다. 이것이 바로 negative log likelihood이다.

\[\theta^* = argmin_\theta \ log[p(y \lvert f_\theta(x))]\\ loss : -\log \ p(y \lvert f_\theta(x))\]

back propagation을 통해 네트워크를 업데이트하는 딥러닝에서는 loss function이 다음 두 가지 조건을 만족해야 한다.

1. 전체 data의 loss는 각 sample loss의 총합과 같다.
2. 네트워크의 출력값으로만 loss를 구해야 한다.

negative log likelihood를 아래와 같이 표현하면

\[-\log \ p(y \lvert f_\theta(x)) = - \Sigma_i \log \ p(y_i \lvert f_\theta(x_i))\]

두 가지 조건을 모두 만족한다는 것을 확인할 수 있다.

Loss function: MSE & Cross-Entropy

MSE

위에서는 \(p(y_i \lvert f_\theta(x_i))\)를 가우시안 분포로 가정했었다. 이 경우 수식을 전개해보면 MSE와 같다는 것을 알 수 있다.

\[\begin{multline} \shoveleft if \ f_\theta(x_i) = \mu_i, \sigma_i = 1, \\ \shoveleft p(y_i \lvert \mu_i, \sigma_i) = {1 \over \root \of {2\pi\sigma_i}} \exp(- {(y_i - \mu_i)^2 \over {2 \sigma_i^2}}) \\ \shoveleft \ \ ...\\ \shoveleft - \log p(y_i \lvert \mu_i, \sigma_i) \varpropto {(y_i - \mu_i)^2 \over 2} = {(y_i - f_\theta(x_i))^2 \over 2} \end{multline}\]

Cross Entropy

가우시안 외에도 베르누이 분포로 가정할 수도 있는데 이 경우 Cross Entropy 수식과 동일해진다.

\[\begin{multline} \shoveleft if \ f_\theta(x_i) = p_i, \\ \shoveleft p(y_i \lvert p_i) = p_i^{y_i}(1-p_i)^{1 - y_i} \\ \shoveleft \ \ ...\\ \shoveleft - \log p(y_i \lvert p_i) = - [y_i \log(p_i) + (1 -y_i) \log(1 - p_i)] \end{multline}\]

결과적으로 딥러닝에서 사용되는 두 가지 loss function은 maximum likelihood 관점에서 보면 어떤 확률분포의 모수를 추정하느냐에 대한 차이라고 할 수 있다.

Reference

• 이활석 님의 오토인코더의 모든 것
• 블로그 bskyvision