Pytorch-Geometric Introduction
- update date: 2020.09.11
- Environment Setting: Mac OS(10.15.4), python(3.6.8), torch(1.6.0)
- PyTorch geometric 홈페이지
- PyTorch geometric 설치 페이지
- PyTorch geometric Example
Introduction
PyTorch-Geometric 홈페이지에 들어가 보면 PyTorch-Geometric을 Geometric Deep Learning을 위한 Extention이라고 소개하고 있다. 그렇다면 Geometric Deep Learning은 무엇일까. 2020년 9월 기준으로 인용 수가 1100회가 넘는 논문 Geometric deep learning: going beyond Euclidean data에서는 다음과 같이 정의한다.
- Geometric deep learning is an umbrella term for emerging techniques attempting to generalize (structured) deep neural models to non-Euclidean domains such as graphs and manifolds
쉽게 말해 Non-Euclidean Domain의 문제들을 Deep Learning으로 해결하는 방법에 대해 연구하는 분야이며, 그것의 대표적인 예로 Graph가 있다는 것이다. PyTorch-Geometric은 이러한 문제들을 PyTorch를 통해 쉽게 구현할 수 있도록 도와주는 도구라고 생각할 수 있다.
Installation
PyTorch-Geometric을 설치하기 위해서는 PyTorch-Geometric뿐만 아니라 몇 가지 부가적인 패키지들이 필요하다. 홈페이지에 따르면 다음과 같이 pip로 모두 설치할 수 있다고 한다.
pip install torch-scatter==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-${TORCH}.html
pip install torch-sparse==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-${TORCH}.html
pip install torch-cluster==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-${TORCH}.html
pip install torch-spline-conv==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-${TORCH}.html
pip install torch-geometric
위에서 ${CUDA}에는 자신의 CUDA Version에 맞는 값을, ${TORCH}에는 자신의 Torch Version에 맞는 값을 채워 넣으면 된다. 예를 들어 CUDA 10.2를 쓰고 있다면 cu102를, Torch 1.6.0을 쓰고 있다면 1.6.0를 사용하면 된다.
pip install torch-scatter==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.6.0.html
pip install torch-sparse==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.6.0.html
pip install torch-cluster==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.6.0.html
pip install torch-spline-conv==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.6.0.html
pip install torch-geometric
사실 그냥 이렇게 해도 된다.
pip install torch-scatter torch-sparse torch-cluster torch-spline-conv torch-geometric
최종적으로 설치된 패키지의 버전은 다음과 같다.
torch (1.6.0)
torch-cluster (1.5.7)
torch-geometric (1.6.1)
torch-scatter (2.0.5)
torch-sparse (0.6.7)
torch-spline-conv (1.2.0)
Graph Data
Torch-Geometric에서 Graph를 만드는 가장 기본적인 방법은 다음과 같이 Data Class를 사용하는 것이다. 예제에 사용된 코드는 모두 PyTorch geometric Example를 참고했다.
import torch
from torch_geometric.data import Data
edge_index = torch.tensor([[0, 1, 1, 2, 1, 3],
[1, 0, 2, 1, 3, 1]], dtype=torch.long)
x = torch.tensor([[-1], [0], [1], [3]], dtype=torch.float)
data = Data(x=x, edge_index=edge_index)
print(data) # Data(edge_index=[2, 6], x=[4, 1])
print(data.num_nodes) # 4
print(data.num_edges) # 6
print(data.is_directed()) # False
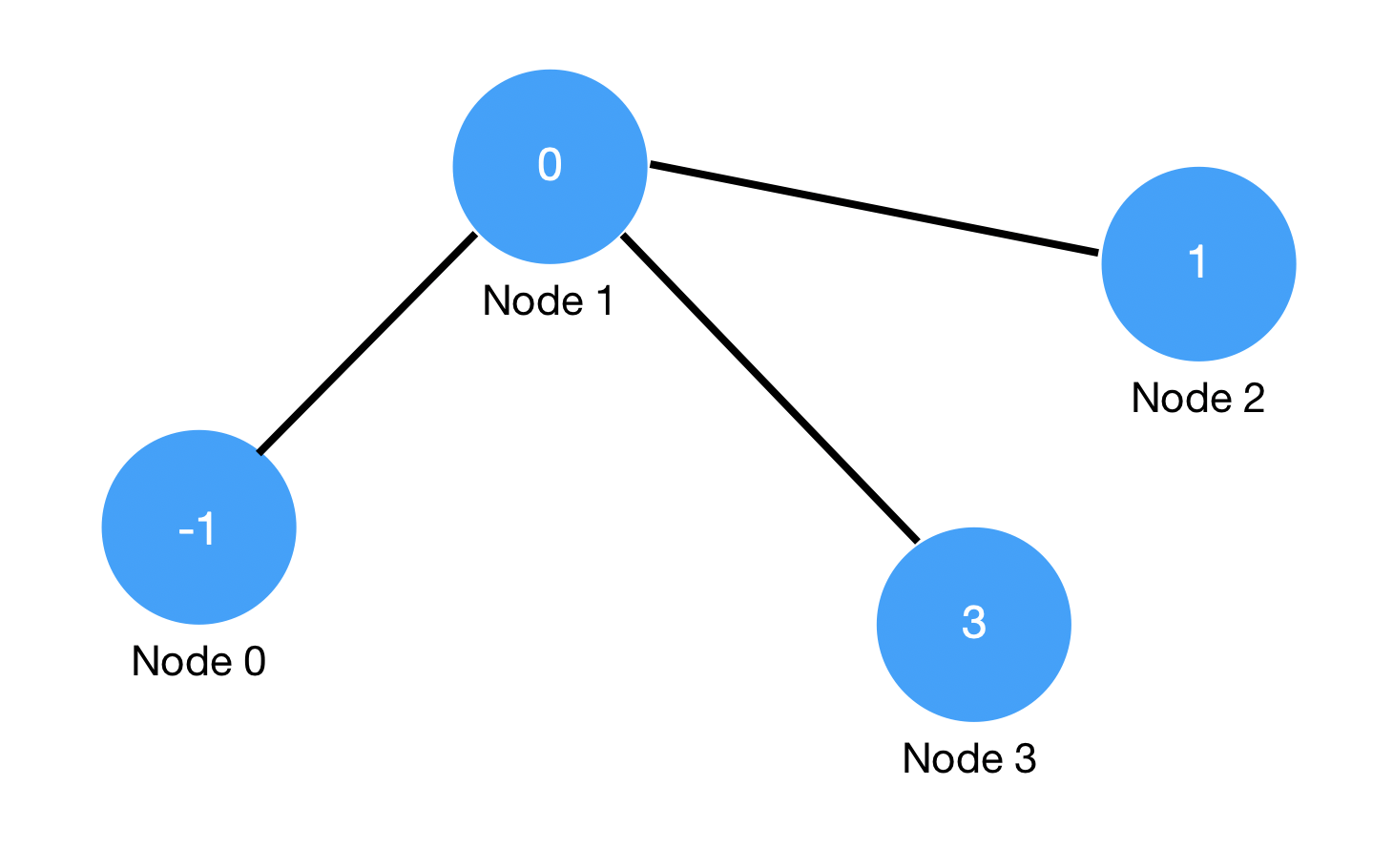
위의 코드는 이미지와 같이 Node의 개수가 4개이고, Edge의 개수가 3개인 Undirected 그래프를 표현한 것이다. edge_index에는 각각의 Edge가 연결하는 Node의 Index 정보가 포함되는데, Undirected Graph는 양방향 Edge로 표현하므로 코드에서는 3개의 Edge를 표현하기 위해 총 6개의 Edge가 사용되었음을 확인할 수 있다.
x는 Feature Matrix라고 할 수 있으며 각 Node의 Feature가 Row로 담기게 된다. 코드에서는 4개의 Node가 있고, 각 Node의 Feature가 \(1 \times 1\)이기 때문에 x.shape는 \((4, 1)\)이 된다.
각각의 Edge를 row로 확인하기 쉽게 다음과 같이 표현하고 Transpose하여 전달하는 것도 가능하다. Transpose 하지 않으면 의도하는 Graph와는 다르게 만들어지므로 유의해야 한다.
edge_index = torch.tensor([[0, 1],
[1, 0],
[1, 2],
[2, 1],
[1, 3],
[3, 1]], dtype=torch.long)
x = torch.tensor([[-1], [0], [1], [3]], dtype=torch.float)
data = Data(x=x, edge_index=edge_index.t())
Dataset
Graph 문제와 관련하여 가장 많이 사용되는 Baseline Dataset으로 Cora가 있다. Cora Dataset 홈페이지에 따르면 Cora Dataset을 2708개의 scientific publications 간의 관계를 Graph로 표현하는 데이터셋이라고 하며 다음과 같은 사양을 가지고 있다.
- Number of Nodes: 2708
- Number of Edge: 5429
- Size of Node Feature: 1433
- Mumber of Class: 7
그리고 전체 데이터셋은 Train/Valid/Test Node로 미리 구분되어 있다.
- Number of Train Node: 140
- Number of Valid Node: 500
- Number of Test Node: 1000
코드를 통해 확인하면 다음과 같다.
from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='./dataset/', name='Cora')
print(len(dataset))
# 1
print(dataset.num_classes)
# 7
print(dataset.num_node_features)
# 1433
data = dataset[0]
print(data)
# Data(edge_index=[2, 10556],
# test_mask=[2708],
# train_mask=[2708],
# val_mask=[2708],
# x=[2708, 1433],
# y=[2708])
print(data.is_undirected())
# True
print(data.train_mask.sum().item())
# 140
print(data.val_mask.sum().item())
# 500
print(data.test_mask.sum().item())
# 1000
Graph Convolution Netork with Torch
마지막으로 PyTorch geometric Example에서는 다음과 같이 GCN을 구현하고 있다(Net에 아주 약간의 변화를 주었다). 각 GCN Layer는 전체 Feature Matrix x와 edge_index를 입력으로 받아 Feature Size가 다른 새로운 Feature Matrix를 출력하게 된다. 예를 들어 아래 Net에서 첫 번째 layer conv1은 cora dataset의 각 Node Feature를 1433에서 16으로 줄여준다. 이외 학습 과정은 torch의 일반적인 학습 방식과 동일하다.
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid
class Net(torch.nn.Module):
def __init__(self, num_node_features, num_classes):
super(Net, self).__init__()
self.num_node_features = num_node_features
self.num_classes = num_classes
self.conv1 = GCNConv(num_node_features, 16)
self.conv2 = GCNConv(16, num_classes)
def forward(self, data):
x, edge_index = data.x, data.edge_index
x = self.conv1(x, edge_index)
x = F.relu(x)
x = F.dropout(x, training=self.training)
x = self.conv2(x, edge_index)
return F.log_softmax(x, dim=1)
dataset = Planetoid(root='./dataset/cora', name='Cora')
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(dataset.num_node_features, dataset.num_classes).to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
model.train()
for epoch in range(200):
optimizer.zero_grad()
out = model(data)
loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
model.eval()
_, pred = model(data).max(dim=1)
correct = int(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / int(data.test_mask.sum())
print('Accuracy: {:.4f}'.format(acc)) # Accuracy: 0.8000