논문 제목 : VLSI Cell Placement Technique
- K. SHAHOOKAR, P. MAZUMDER
- 1991
- 논문 링크
- 2020.09.07 정리
- 논문이 약 78p로 길기 때문에 필요한 부분만 정리했습니다.
Keywords
- VLSI: Very Large Scale Integration의 약자로 우리 말로는 초고밀도 집적회로라고 한다.
Cell Placement Problem
Cell Placement 문제란 CPU를 비롯한 반도체를 구성하는 여러 개의 하위 요소(Module)들을 Chip Canvas 상에 어떻게 배치할 것인지 결정하는 문제를 말한다. 간단해 보이지만 크기가 모두 다르고 적게는 수백 개 부터 많게는 수만 개에 이르는 하위요소들을 배치하면서 WireLenght, Chip Canvas Size 등과 같은 비용을 최소화하는 해를 찾는 것은 결코 쉬운 문제가 아니다. 수학적으로도 Cell Placement의 최적 해를 찾는 것은 NP complete 문제로 알려져 있다.
Chip Placement가 어려운 이유 중 하나는 Module을 배치하는 데 있어 각 Module 간의 연결을 고려하여야 한다는 점이다. 이러한 점에서 어떤 Cell을 디자인한다는 것은 주어진 Circuit Diagram에 따라 서로 다른 특성을 가지는 각각의 모듈을 어떻게 연결할 것인지 결정하는 것이라고 할 수 있다. 구체적으로 Chip Placement 문제는 다음과 같이 정의된다.
- Input: (1) 각 Module의 특성(크기, 기능 등) (2) Netlist(Module 간의 연결구조)
- Output: (1) 각 모듈의 x,y 좌표
- Objective: (1) Chip Area (2) WireLength
참고로 입력 중 하나인 Netlist(좌측)와 출력인 Modue Coordiate(우측)는 다음과 같다.
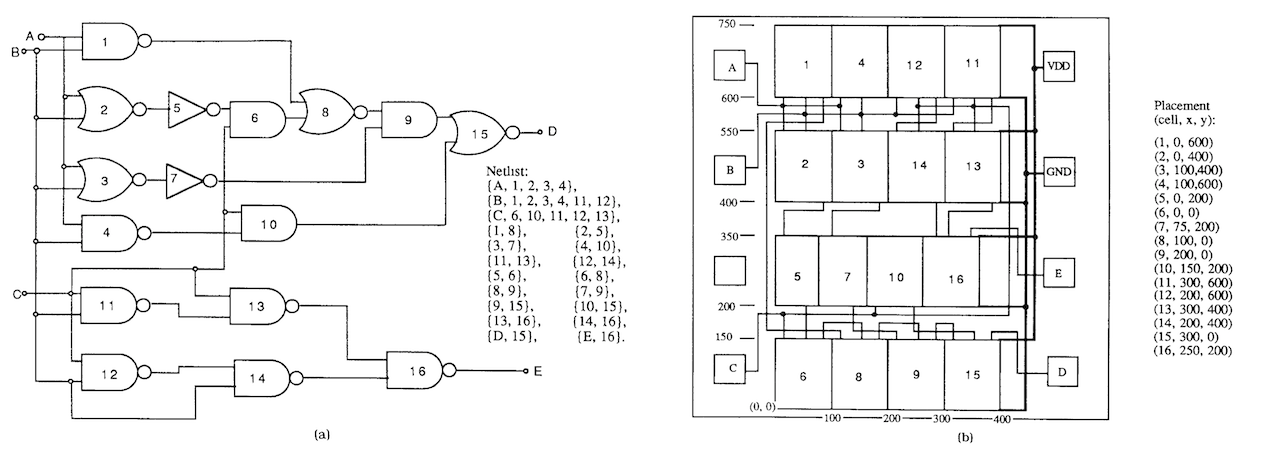
Module을 배치하는 것과 관련하여 한 가지 더 고려해야 할 점이 있다면 물리적 타당성(phisically possible)이다.
- 각 Module은 서로 겹치면 안 된다.
- Chip의 경계 내에 Module이 존재해야 한다.
등이 대표적이며, 문제의 유형에 따라 다른 제약 조건이 추가될 수 있다.
Standard Cell & Macro
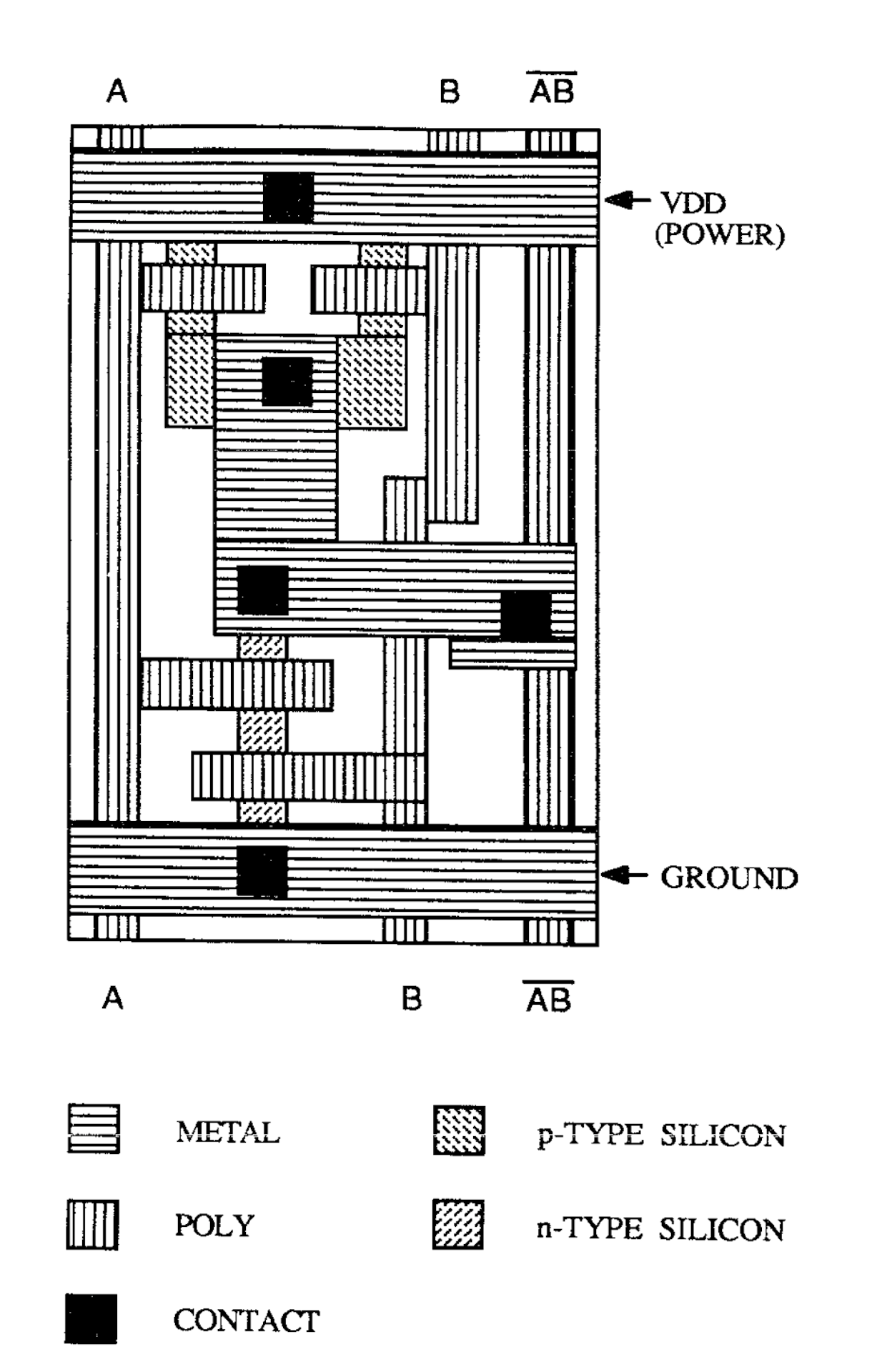
Cell Placement 문제에서 배치의 대상은 Standard Cell과 Macro 두 가지이다. Standard Cell은 내부 디자인이 고정된 논리 모듈로 쉽게 말해 XOR Gate, NOR Gate 등과 같은 Logic Module 등을 지칭한다. 모든 Standard Cell은 일정한 높이를 가지지만 기능에 따라 다른 크기를 가진다. Macro Module은 Standard Cell과는 다른 Format을 가지는 Module로, 보다 복합적인 기능을 수행하고 Standard Cell과 비교해 크기가 일반적으로 더 크다.
우측 그림은 Standard Cell의 내부 구조로, 그림에서 확인할 수 있듯이 Module이 제 기능을 수행하기 위해서는 입력과 출력 Terminal(pin))이 다른 Module 또는 Chip의 입력 및 출력과 연결되어야 한다. 이러한 연결을 Wire라고 하며, Module을 배치할 때에는 Wire가 지나가게 될 공간(Routing Channel)을 고려해야 한다. 참고로 논문에서 사용하는 용어 및 동의어를 정리하면 다음과 같다.
- Standard Cell: Grid Cell, Cell, Module, Element
- Macro Block: Macro, Block
- Wire: Net, Interconnect, Signal Line
- Terminal: Terminal of Module, Pin
- Pad: Terminal of Chip
- Placement: Configuration, Solution
Various Types of Problems
논문에서는 Cell Placement 문제를 다음과 같이 세 가지로 나누어 유형화하고 있다.
(1) Placing and Connecting Standard Cell and Macro
서로 다른 크기의 Standard Cell과 Macro를 위와 같이 주어진 영역 내에 배치하는 것이다. Macro의 크기가 더 크기 때문에 일반적으로 먼저 배치하게 되고, Standard Cell은 Row의 형태로 묶음 단위로 배치된다는 특성을 가진다.
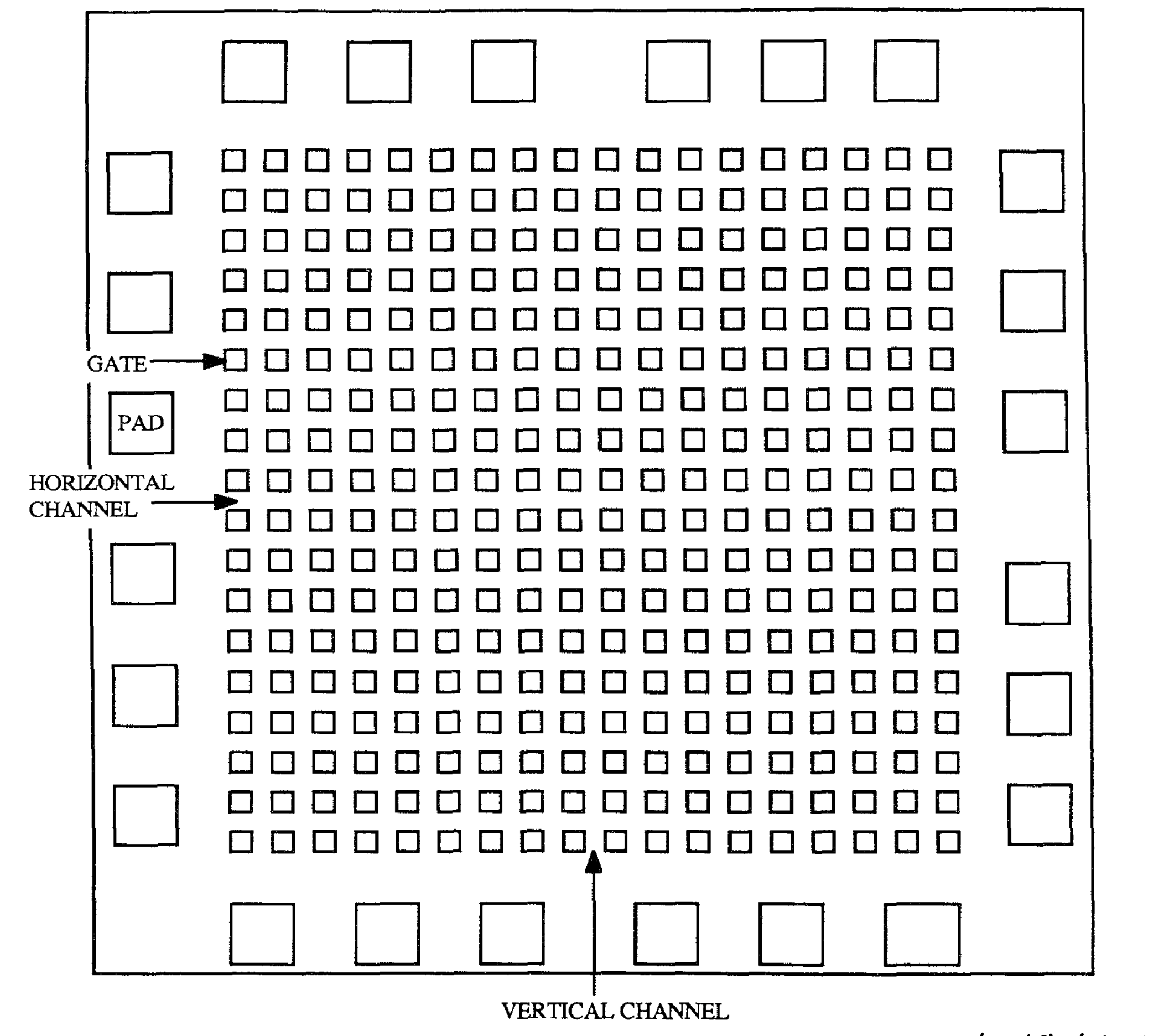
(2) Connecting Grid Standard Cell
Grid 형태로 많은 Standard Cell들이 미리 배치되어 있고, 이들을 어떻게 연결할지 결정하는 문제이다.
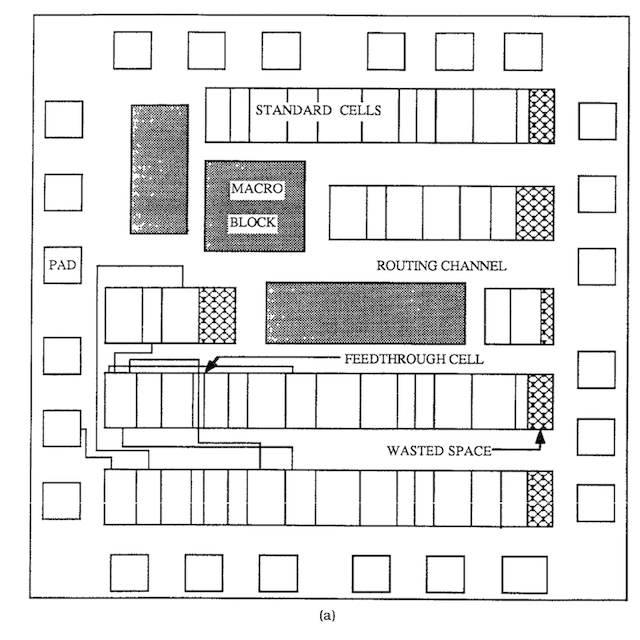
(3) Placing and Connecting Macro
Standard Cell 없이 Macro만을 배치하는 문제이다. 각 Macro의 크기와 형태가 모두 다르므로 중간 중간에 낭비되는 공간(Wasted Space)가 있는 것을 확인할 수 있다.
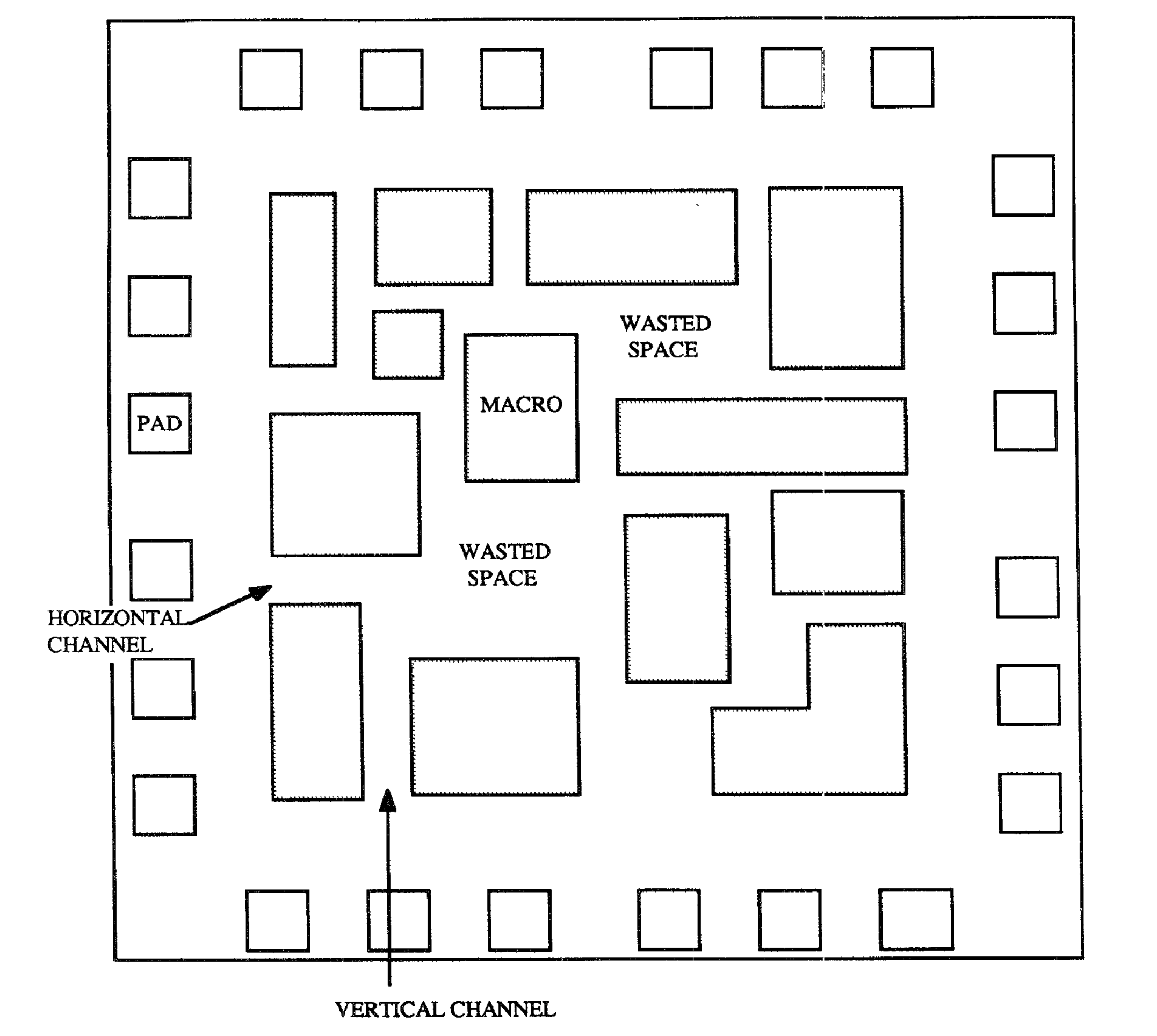
Type and Objective
한 가지 흥미로운 점은 문제의 유형에 따라 두 Objective, Wire Length를 줄이는 것과 Place Area를 줄이는 것 간의 관계가 달라진다는 점이다. Standard Cell을 배치하는 문제와 Grid Standard Cell 문제에서는 Module 간의 길이가 좁으면 좁을수록, 즉 Place Area의 크기가 작으면 작을수록 Wire Length도 줄어들 가능성이 높다. 반면 Macro를 배치하는 경우에는 크기가 모두 다르기 때문에 Wire Length를 줄이는 방향으로만 배치하면 Place Area가 과도하게 커질 가능성이 높다.
Wire Length Estimation
Chip Placement에서 모든 Wire는 수직, 수평의 선분만을 사용하게 되고 Wire가 지나가는 Routing Channel은 두 겹으로 되어 있어 Wire의 수직 요소가 지나가는 층과 수평 요소가 지나가는 층이 분리되어 있는 것이 일반적이다. 이러한 점에서 각 Module을 연결하는 Wire의 거리는 거의 대부분 Manhattan Distance를 기준으로 추정하게 된다. 추정치의 정확도를 높이기 위해서는 Routing Tool이 사용하는 Routing 방식을 알아야 한다.
Routing Methods
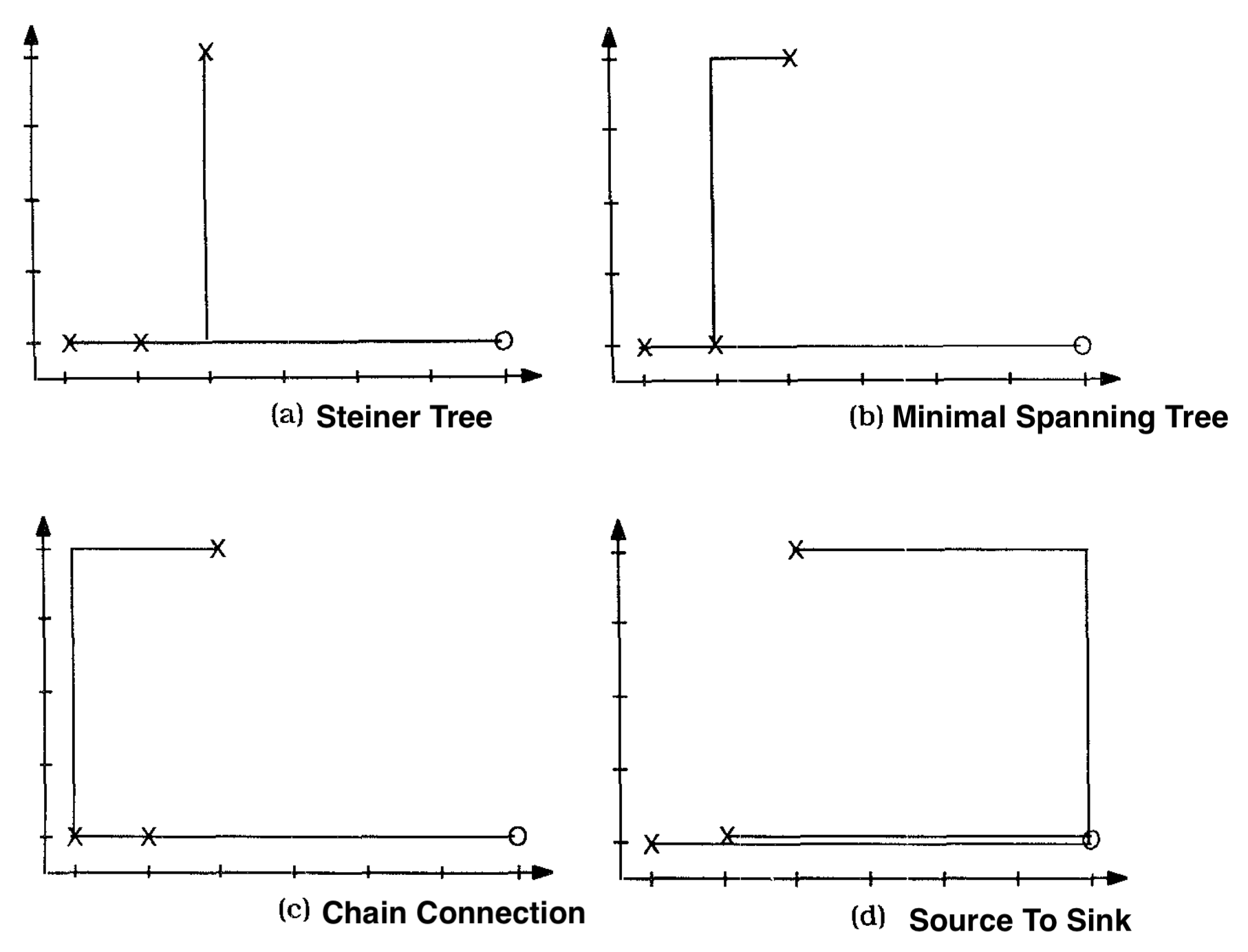
Steiner Tree는 Wire 중간에서 Branch가 분기되어 나올 수 있다는 점이 특징이다. 어디서나 분기되어질 수 있어 전체 Wire의 길이가 가장 짧아질 수 있는 방법이지만, 분기가 이뤄지는 지점과 Branch를 각 Module에 연결하는 방법 모두를 결정해야 하므로 복잡도가 높고 시간이 오래 걸리는 방법이기 때문에 Module의 수가 많고 문제가 복잡하면 할수록 잘 사용하지 않는 방법이다.
Minimal Spanning Tree 방법은 Pin에서만 분기되어 나올 수 있는 방법이고, Chain Connection은 말 그대로 Branch가 존재하지 않고 전체 Wire가 하나의 Chain처럼 이어져 있는 방법이다. Chain Connection의 경우 과도하게 Wire의 길이가 일어지는 경향을 보인다고 한다. 마지막으로 Source To Sink Connection이 있는데 이 방법은 Chip의 PAD와 모든 Module이 직접 연결되는 방법이다. 구현은 가장 간단하지만 결과물은 가장 좋지 않다고 한다.
그림으로 표현하면 아래와 같다.
Semiperimeter Method
Wire Length를 추정하는 가장 기본적인 방법은 Semiperimeter Method이다. Pareimeter, 즉 둘레를 이용하는 방법으로 Wire가 연결하는 Terminal들을 모두 잇는 경계 사각형의 둘레의 절반으로 Wire Length를 추정하게 된다. 이 방법을 사용하면 Terminal의 갯수가 3개 이하인 경우에는 정확하게 Manhattan Distance를 구할 수 있고, 4개 이상 부터는 정확도가 떨어져 33% 정도 짧게 추정하는 경향을 보인다고 한다. Routing 방식에 따라서 추정치의 오차가 달라지는데, Steiner Tree에서 가장 정확하다고 한다.
대부분의 Wire가 2,3개의 Terminal을 연결하게 되고, 그 이외의 경우에도 어느 정도 만족할 만한 수준의 추정치를 내어준다는 점에서 많이 사용된다.
Algorithms
Chip Placement 문제는 NP-Complete 문제, 즉 다항 시간 내에 완벽한 해결책을 찾을 수 없는 문제이다. 가능한 배치의 경우의 수를 하나씩 모두 확인해 보는 방법으로 접근이 가능하지만 배치 대상의 Factorial 만큼의 시간 복잡도를 가지기 때문에 사실상 불가능하다고 할 수 있다. 이러한 Chip Placement 문제와 관련하여 1960년대 부터 휴리스틱을 사용하는 다양한 알고리즘들이 제시되어 왔다. 본 논문에서 다루는 주요 알고리즘으로는 다음과 같은 것들이 있다.
- Simulated Annealing
- Force-Directed Placement
- Min-Cut Placement
- Placement by Numerical Optimization
- Evolution-Based Placement
알고리즘들은 Constructive Placement와 Iterative Improvement 두 가지로 분류할 수 있다. Constructive Placement는 매번 모든 Module들을 새롭게 배치하는 방법을 말하며, Numerical Algorithm, Placement By Partitioning, Force-Directed Method 등이 대표적이다. Iterative Improvement는 초기 배치에서 시작하여 반복적으로 개선하는 방법으로 Simulated Anealing, Force-Directed Method 등이 있다. Force-Directed Method는 두 가지 유형 모두에 맞춰 적용이 가능하기 때문에 모두 포함되었다.
Force-Directed Placement
Force-Directed Placement 방법은 최적의 배치를 달성하기 위해 Module을 어디에 위치시켜야 하는지 결정하는 방법이다. 1960년대에 처음 제안되었고, 구현 방식이 매우 다양하여 Constructive Placement로 접근하는 경우와 Iterative Improvement로 접근하는 경우 모두 존재한다.
예를 들어 Module들이 모두 배치되어 있는 초기 배치가 존재하고, 각각의 Module 간에는 다음 공식에 따라 결정되는 Force의 크기에 비례하여 서로 끌어당기는 힘이 있다고 가정하자. 여기서 \(w_lj\)는 Module \(l\)과 \(j\)를 연결하는 wire가 가지는 가중치이고, \(s_lj\)는 두 모듈 간의 거리를 의미한다.
\[F_l = \Sigma_{j} w_{lj} s_{lj}\]이때 만약 Module들이 힘의 방향에 따라 자유롭게 이동할 수 있다면 Minumum Energy State를 가지는 균형 상태를 맞출 수 있을 것이다. Force-Directed Placement는 이러한 방식에 따라 각 Module의 위치를 결정한다. 이때 개별 Module의 Force가 0, 균형상태에 있게 되는 지점을 Target Point라고 하며 다음과 같이 정해진다.
\[\{ x_l \}_{F=0} = {\Sigma_j w_{lj} x_l \over \Sigma_j w_{lj}} = \bar x_l\\ \{ y_l \}_{F=0} = {\Sigma_j w_{lj} y_l \over \Sigma_j w_{lj}} = \bar y_l\]Constructive Method for Force-Directed
Constructive Method라는 표현에 맞게 초기 배치가 주어지지 않으며, 각 Module의 좌표를 변수로 하고 모든 Moduledml Force가 0이 되도록 하나씩 배치하는 방법이다. 반복적으로 해를 구하게 되는데, 이때 동일한 해를 찾지 않도록 하는 것이 중요하다.
Iterative Improvement for Force-Directed
Iterative Improvement에서는 임의로 또는 Constructive Method를 통해 결정된 초기 배치에서 시작해, 배치된 Module 중에 하나를 골라 Force를 계산하여 Target Point로 Module을 이동시키게 된다. 여기서 옮길 Module을 고르는 방법부터 Target Point를 점유하고 있는 다른 Module이 있는 경우 대처 방법 등과 같이 구체적인 구현 내용과 다음 다섯 가지 방법을 제시하고 있다.
- 임의로 혹은 Force가 가장 큰 Module을 선택하고 Target Point를 차지하고 있는 Module과 위치를 바꾸는 방법. 이때 Target Point가 비어 있는 경우라면 Module을 선택하는 것부터 다시 시작한다.
- 임의로 혹은 Force가 가장 큰 Module을 선택하고 Target Point를 차지하고 있는 Module과 위치를 바꾸었을 때와 그러지 않았을 때의 Cost(Wire Length)를 비교하여 교체 여부를 결정하는 방법.
- 임의로 혹은 Force가 가장 큰 Module을 선택하고 이를 Target Point로 옮긴 뒤 기존에 차지하고 있던 Module의 Target Point를 구해 연쇄적으로 옮기는 방법
- 모든 Module의 Target Point를 구한 다음 서로 자리 교체를 했을 때 보다 Target Point에 가까워지는 쌍을 찾아 옮기는 방법
- 두 Module을 임의로 골라 바꾸었을 때와 그러지 않았을 때의 Cost를 비교해보고 바꾸는 것이 더 좋을 때에만 서로 위치를 교체하는 방법.
다음은 4번 째 알고리즘의 sudo code이다.

위 알고리즘에서 어떤 두 Module의 Target Point가 일치하면 계속해서 서로 자리를 바꾸게 된다. 이 경우 lock을 걸게 되는데, 이러한 방식으로 너무 많은 Module들에 lock이 걸리게 되면 모든 lock을 해제한 후 임의의 Module 부터 새로 시작한다. 이와 같이 각 알고리즘의 구체적인 내용은 서로 다르게 구현될 수 있다.