Python Bulit-in Time Complexity: List
- Python Data Structures
- Python Wiki-Time Complexity
- Update at : 20.12.07
Introduction
Python에서는 Bulit-in Data Type으로 List, Set, Dictionary 등을 제공하고 있다. 이들은 각각의 특성에 맞게 필요에 따라 달리 사용되는데, 단순히 List는 중복을 허용하고 Set은 그렇지 않다는 표면적인 특성 외에도 Data Type에 따라 동일한 연산에 대해서도 시간 복잡도가 달라질 수 있어 이 또한 고려하여 선택하는 것이 좋다.
Python Wiki-Time Complexity에서는 Python Interpreter 중 하나인 cpython을 사용하는 경우 각 Data Type의 연산들에 대한 시간 복잡도를 확인할 수 있다. 여기서는 cpython을 기준으로 이와 같은 시간 복잡도 계산이 어떻게 구해진 것인지 확인해보고자 한다.
List: Dynamic Array
| Opertaion | Average Case | Amortized Worst Case | Worst Case |
|---|---|---|---|
| indexing | \(O(1)\) | \(O(1)\) | \(O(1)\) |
| search | \(O(n)\) | - | \(O(n)\) |
| copy | \(O(n)\) | \(O(n)\) | \(O(n)\) |
| append | \(O(1)\) | \(O(1)\) | \(O(n)\) |
| insert | \(O(n)\) | \(O(n)\) | \(O(n)\) |
| remove | \(O(n)\) | \(O(n)\) | \(O(n)\) |
| pop | \(O(1)\) | \(O(1)\) | \(O(1)\) |
Average Case, Amortimzed Case 그리고 Worst Case는 어떤 연산의 시간 복잡도를 구하는 방법들이다. 여기서 Average Case와 Worst Case는 이름이 가지는 의미 그대로 각각 가능한 모든 경우에 있어 평균적인 시간 복잡도와 최악의 경우 시간 복잡도를 의미한다. 두 가지에 비해서는 다소 복잡한 Amortimzed Case는 쉽게 말하면 연산 Sequence 상에서 Worst Case가 어떤 비중으로 발생하는지 고려하여 시간 복잡도를 산정하는 방식이다. Worst Case가 분명 존재하지만 전체 연산 Sequence에서 매우 드문 간격으로 한 번씩 발생한다면 그 중요도를 상각(amortize)할 필요가 있다는 이유에서 고안되었다고 한다.
여기서 Average Case는 Python Wiki-Time Complexity의 내용을 참고했지만 Worst Case는 직접 계산한 결과이다. 따라서 오류가 있을 수 있다.
List is Dynamic Array
Python의 List는 Dynamic Array로 구현되어 있다. 기본적으로 Array는 메모리 상에 연속적으로 저장되어있는 데이터 집합을 지칭하는데, 아래 C 코드로 Array의 원소들이 메모리상에서 저장된 위치를 확인해보면 명확하게 알 수 있다.
int main()
{
int array[5] = {0,};
int* ptr0 = &array[0];
int* ptr1 = &array[1];
int* ptr2 = &array[2];
int* ptr3 = &array[3];
int* ptr4 = &array[4];
printf("array[0] %p\n", ptr0);
printf("array[1] %p\n", ptr1);
printf("array[2] %p\n", ptr2);
printf("array[3] %p\n", ptr3);
printf("array[4] %p\n", ptr4);
return 0;
}
array의 각 element의 주소값을 출력하는 코드로 실행 결과는 다음과 같다.
array[0] 0x7ffee57c07c0
array[1] 0x7ffee57c07c4
array[2] 0x7ffee57c07c8
array[3] 0x7ffee57c07cc
array[4] 0x7ffee57c07d0
C에서 Integer의 크기는 4바이트 이므로 array에서 접근하고자 하는 index가 1 증가할 때마다 4씩 주소값이 커짐을 알 수 있다. 보다 구체적으로 int array[5] = {0,};는 5개의 Integer를 저장할 메모리 공간을 연속적으로 할당하고, 그 값은 모두 0으로 채워넣겠다는 것을 의미한다고 할 수 있다. 필요한 메모리의 크기가 고정적이고, 그 크기는 코드만으로도 알 수 있기 때문에 컴파일 타임에 array의 크기가 결정된다. 이러한 점에서 이와 같은 array를 Static Array라고 한다.
그런데 이러한 Static Array를 그대로 적용하여 Python의 List를 구현하는 것은 쉽지 않다. 왜냐하면 Python의 List는 새로운 element를 추가하는 append 등의 연산을 제공하므로 한 번 선언된 이후에도 크기가 커질 수 있어야 하기 때문이다. 이러한 문제 때문에 Python의 List는 Static Array가 아닌, 런타임에 크기를 달리할 수 있는 Dynamic Array로 구현되어 있다.
Dynamic Array: How to change the size of array?
그렇다면 Dynamic Array는 어떻게 가변적인 크기를 가질 수 있을까. 저장하고자 하는 데이터의 개수가 가변적인 상황에서 사용할 수 있는 자료구조의 가장 대표적인 예시로 Linked List가 있다. 이를 사용하면 사용할 수 있는 메모리가 가득 찰 때까지 계속해서 새로운 element를 저장하는 것이 가능하다. 그런데 이는 Array의 정의, 모든 데이터가 연속적으로 할당된다는 특성을 만족하지 못한다. Dynamic Array도 엄연한 ‘Array’이기 때문에 항상 데이터들이 연속적으로 메모리 공간을 점유해야 하는 형태로 구현되어 있다.
이것이 가능한 이유는 Dynamic Array에서는 런타임에 List의 크기를 넘어서 element를 추가하고자 하면 전체 List를 통째로 복사하여 새롭게 할당해버리기 때문이다(위키). 아래 그림을 보면 보다 쉽게 이해할 수 있다.
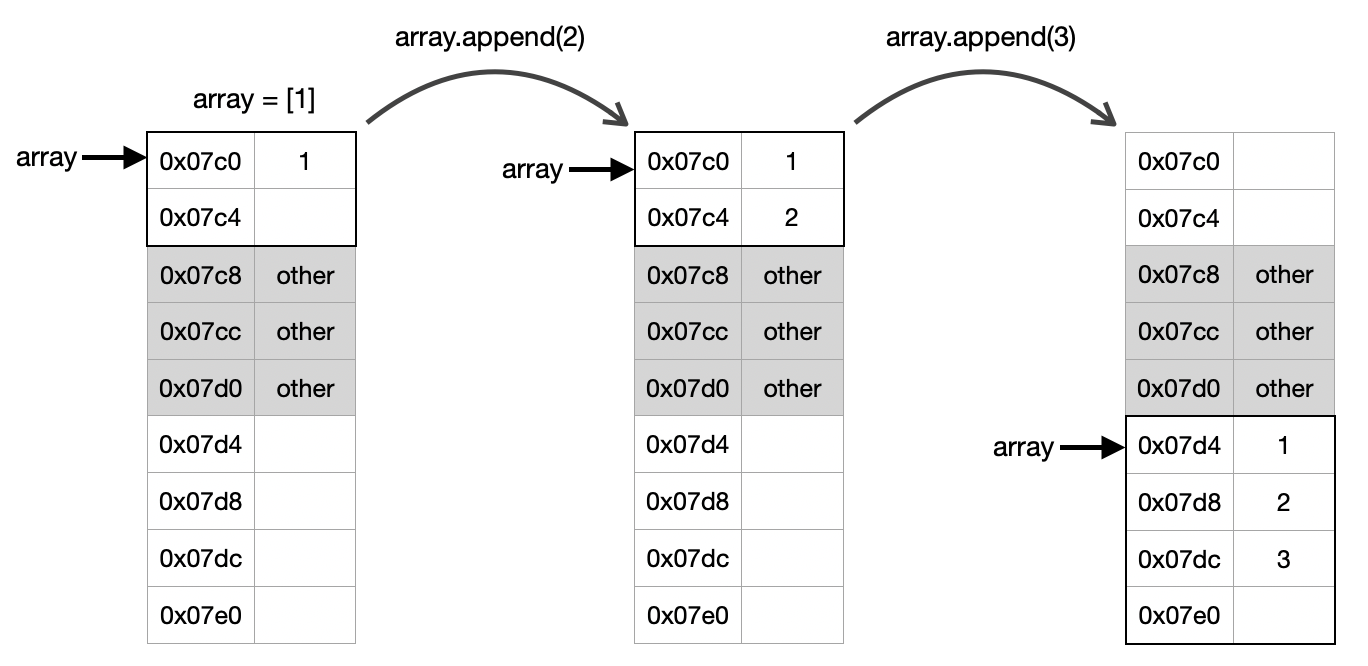
즉, 현재 할당된 크기를 넘어서 새로운 element를 추가하게 되면 더 큰 메모리 공간을 할당하는 방식으로 Dynamic Array는 동작하게 된다. 참고로 Python List의 구체적인 재할당 방식은 cpython에서 List의 동작 방식을 정의하는 listobject.c의 list_resize(PyListObject *self, Py_ssize_t newsize)함수를 보면 보다 구체적으로 확인할 수 있다.
이와 같은 저차원적인 내용이 중요한 이유는 시간 복잡도 계산에 직접적으로 고려해야 하는 요소로 작용하기 때문이다. 즉 뒤에서 확인할 수 있겠지만 List의 append, insert와 같이 새로운 element를 추가하는 연산의 시간 복잡도 계산에는 재할당에 따른 시간 복잡도 또한 포함된다.
Indexing
List는 Dynamic Array이기 때문에 모든 구성 요소들의 위치를 다음과 같이 쉽게 계산할 수 있다.
\[\text{element address = start address + (index }*\text{ element size)}\]따라서 Indexing에서는 최악의 경우에도 \(O(1)\)이 걸린다.
Search
어떤 값이 List 내에 없다고 확신하기 위해서는 모든 Element를 확인해보아야 한다. 따라서 최악의 경우에는 \(O(n)\)이 된다. 평균적인 시간 복잡도는 다음과 같이 계산된다.
\[{1+2+...+n \over n} = {n(n+1) \over 2n} = {n+1 \over 2}\]풀이하자면 분자에는 첫 번째 Index의 element를 탐색하는 경우 시간 시간복잡도(\(1\))부터 두 번째(\(2\)), 세 번째(\(n\)), 마지막 element의 원소를 찾는 경우까지, 가능한 모둔 경우의 시간 복잡도의 총합이 들어가고 분모에는 탐색의 경우의 수인 \(n\)이 들어가게 된다. 이를 계산해보면 \({n+1 \over 2}\)이 나오게 되고, Big-O 표기법에 따라 \(O(n)\)이 된다.
Copy
List를 복사할 때에는 전체 element를 하나씩 복사해야 하기 때문에 \(O(n)\)이 된다.
Append
앞서 언급했듯이 Append와 같이 새로운 element를 추가하는 연산의 경우 Dynamic Array의 특성을 고려하여 시간 복잡도를 계산하게 된다. append를 \(n\)번 반복한다고 한다면 언제마다 재할당 할지에 따라 달라지겠지만 다음 그림과 같은 경우를 생각해 볼 수 있을 것이다.
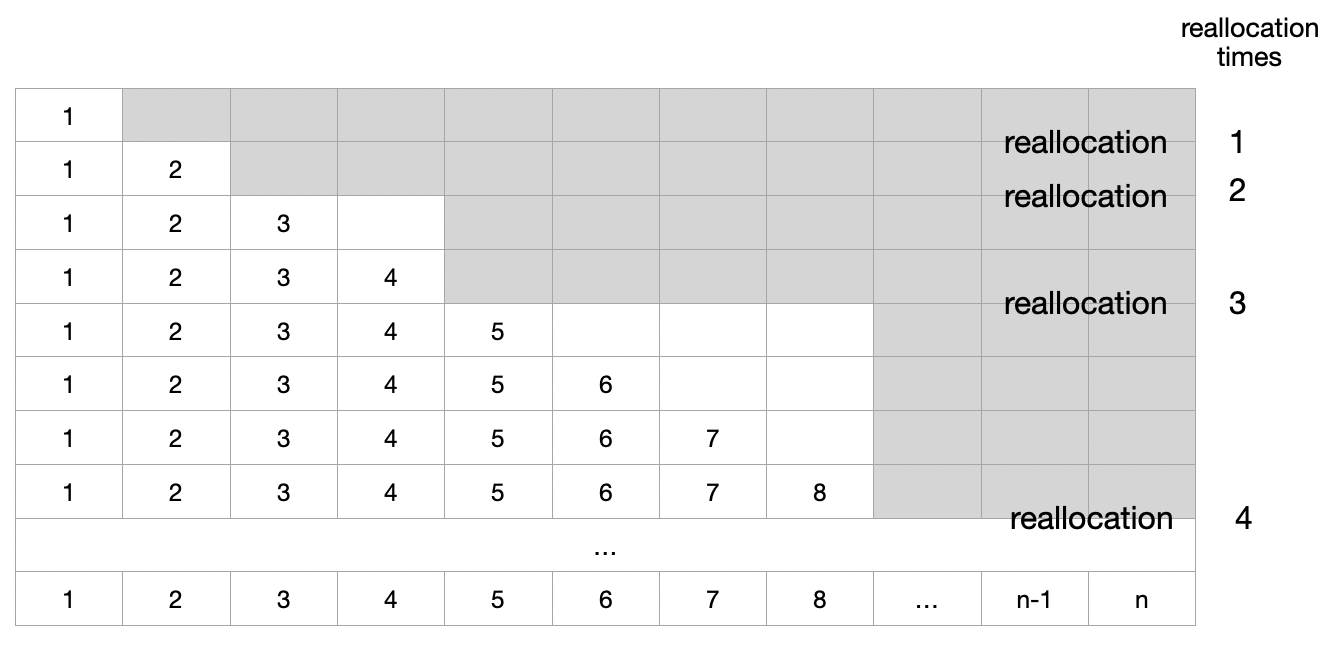
이때 Worst Case는 Append를 하기 위해 재할당을 해야만 하는 경우로, 전체 element를 일일이 복사해야 하기 때문에 시간 복잡도가 \(O(n)\)이 된다. 그 이외의 경우에는 항상 맨 마지막 Index에 element를 추가만 해주면 되기 때문에 \(O(1)\)이다. Average Case를 구하기 위해서는 재할당이 이뤄지는 경우와 그렇지 않은 경우의 횟수를 알아야 하는데, append를 통해 element의 개수가 1개부터 \(n\)개가 될 때까지 재할당이 이뤄지는 횟수를 \(k\)라고 한다면 총 연산 횟수는 다음과 같다.
\[\eqalign{ &1 + 1(\text{reallocation})\\ &+ 1 + 2(\text{reallocation})\\ &+ 1 + 1 + 4(\text{reallocation})\\ &+ 1 + 1 + 1 + 1 +8(\text{reallocation})\\ &+ ...\\ = &n + (2^k - 1) \\ \because & 2^{k-1} \leq n < 2^k, \quad 1+2+...+2^{k-1} = 2^k-1 }\]따라서 Dynamic Array에 \(n\)개의 element를 append 하는 데에 소요되는 시간 복잡도는 \(O(n)\)이 되며, 결과적으로 한 번의 append 연산에 대한 시간 복잡도는 \(O(1)\)이 된다고 할 수 있다.
Insert
항상 맨 마지막에 element를 추가하는 Append 연산과 달리 Insert는 원하는 index에 새로운 element를 추가하게 된다. 이때 Dynamic Array의 특성 때문에 새로운 element를 중간에 추가하기 위해서는 삽입 index 이후의 모든 element들의 저장 위치를 한 칸씩 뒤로 옮겨야 한다.
이를 고려할 때 가장 좋은 경우는 재할당이 없으면서도 마지막 index 다음에 추가하는 경우이다. 이 때의 시간 복잡도는 \(O(1)\)이다. Worst Case는 index 0에 추가하면서 동시에 재할당을 해야 하는 경우이다. 이때의 시간 복잡도는 \(O(n)\)이다. 재할당이 이뤄지는 경우를 제외하고 0번 index부터 마지막 index까지 Insert에 드는 연산 비용은 다음과 같다. 참고로 아래 소괄호 중 첫 번째는 추가에 필요한 연산, 두 번째는 이후 element를 넘기는 연산을 의미한다.
\[\eqalign{ &(1 + n) + (1 + n-1) + ... (1 + 1) + (1 + 0) \\ =& n + {n(n+1) \over 2} \\ =& {n^2 + 3n \over 2} }\]\(n+1\)번 모든 가능한 index에 대한 Insert 연산의 총 시간 복잡도는 \(O(n^2)\)이다. 따라서 Insert 연산의 Average Case는 \(O(n)\)이다.
Remove
특정 element를 제거하는 Remove 연산은 우선 Search로 원하는 element를 찾아야 하고, 찾은 후에는 삭제 후 이후 element들을 모두 한 칸씩 앞으로 당겨 저장해야 한다. 따라서 0번에 위치하고 있는 경우부터 마지막에 위차한 경우까지 Remove에 드는 연산 비용은 다음과 같다. 참고로 아래 소괄호 중 첫 번째는 Search에 필요한 연산, 두 번째는 삭제에 필요한 연산, 세 번째는 이후 element를 한 칸씩 당기는 연산을 의미한다.
\[\eqalign{ &(0 + 1 + n) + (1 + 1 + (n-1)) + ... ((n-1) + 1 + 1) + (n + 1 + 0) \\ =& {n(n+1) \over 2} + n + {n(n+1) \over 2} \\ =& n^2 + 2n }\]따라서 Remove의 Average Case는 \(O(n)\)이다.
Pop
pop 연산을 수행하면 List의 마지막 element를 제거하고 이를 반환하게 된다. 이 경우 재할당의 필요성이 없기 때문에 마지막 값을 찾아 제거만 하면 된다. 따라서 indexing 연산과 동일한 시간 복잡도를 갖는다.