Asymptotic Notation

• Introduction to Algorithms 3판을 참고했습니다.
• 고려대학교 박성빈 교수님의 2018년 가을학기 <알고리즘> 강의를 수강했고, 복습을 목적으로 작성했습니다.
• Update at : 20.12.07

Summary

• 점근적 표기법(Asymptotic Notation)은 알고리즘(함수)의 입력이 무한대로 커진다고 할 때 시간/공간 복잡도가 증가하는 속도를 나타낸다.
• 가장 많이 쓰이는 점근적 표기법으로는 점근적 상한이라고도 불리는 Big-O Notation이 있다.
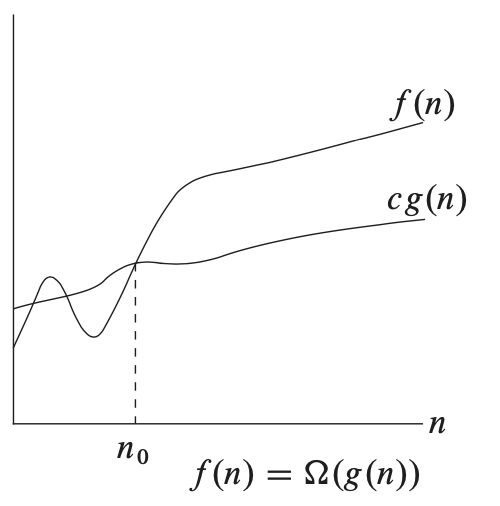
• \(O(g(n))\)은 함수 집합으로서, 모든 \(n \geq n_0\)에 대해 \(0 \leq f(n) \leq c g(n)\)을 만족하는 양의 상수 \(n_0, c\)가 존재하는 함수 \(f(n)\)들의 집합을 말한다.

Introduction

알고리즘(Algorithm)이란 어떤 입력 값을 받았을 때 원하는 출력 값을 반환하도록 하는 일련의 계산 과정을 말한다. 알고리즘 공부를 한다고 하면 자연스럽게 알고리즘 문제를 푸는 것이 떠오르는데, 이러한 알고리즘 문제들은 모두 일정한 규칙을 따르는 입력 값이 주어질 때 그에 따라 결정되는 정답이 항상 출력으로 나오도록 코딩하는 구조로 되어 있다. 이때 어떤 문제를 풀었다고 하기 위해서는 당연히 가능한 모든 입력 값에 대해 항상 정답인 출력을 반환하도록 해야 한다.

그런데 알고리즘을 풀었다고 해서 모든 알고리즘이 같은 수준으로 잘 풀었다고는 할 수 없다. 모두 항상 정답을 반환한다고 할지라도 개중에 더 빠르게 혹은 메모리를 더욱 적게 사용하며 정답을 출력하는 것이 있을 것이다. 즉 각각의 알고리즘이 얼마나 효율적으로 같은 문제를 풀어내는지 또한 중요한 문제가 된다. 이와 같이 알고리즘의 효율성, 컴퓨터 과학의 표현에 따르면 알고리즘의 복잡도를 계산하는 것을 알고리즘 분석(Algorithm Analysis)이라고 한다.

Asymptotic Notation

동일한 기능을 수행하는 여러 알고리즘을 분석하고 서로 비교하기 위해서는 어떤 알고리즘이 얼마나 좋은지에 대한 척도가 필요하다. 이때 가장 많이 사용되는 것이 점근적 표기법(Asymptitic Notation)이다. 점근적 표기법은 기본적으로 입력의 크기가 무한히 커지는 상황에서 알고리즘에 소요되는 시간/공간 복잡도가 증가하는 속도를 나타내는 데에 사용된다. 이때 연산 시간을 측정하여 비교하는 것은 컴퓨터의 성능이나 운영체제, 컴파일러 등의 영향을 받아 환경에 종속적이고, 입력이 무한히 커지는 상황을 가정하고 있어 현실적으로 실측이 불가능하다는 문제점을 가지고 있다. 대신 알고리즘에서 입력의 크기가 커짐에 따라 연산의 횟수가 어떻게 증가하는지를 비교하는 방법을 생각해 볼 수 있는데, 점근적 표기법은 이에 대한 수학적인 표기 방법이다.

점근적 표기법으로는 \(\Theta\)(theta), \(O\)(Big-O), \(o\)(small-O), \(\Omega\)(Big-Omega), \(\omega\)(small-Omega) 총 5가지가 있다. 비슷해 보이지만 약간씩 의미의 차이가 있다. 점근적 표기법으로 나타내고자 하는 것은 함수의 집합들이며, 어떤 알고리즘이 어떤 함수 집합에 포함되는지를 통해 알고리즘의 우열을 가르게 된다. 예를 들어 입력 크기가 \(n\)일 때 어떤 알고리즘의 연산 횟수가 \(f(n)\)이고, 이에 대해 \(f(n) \in O(n)\)이 성립한다면 연산 횟수가 \(g(n) \notin O(n), \in O(n^2)\)인 알고리즘보다 더 좋다고 할 수 있다는 것이다. 여기서는 \(\Theta\)(theta), \(O\)(Big-O), \(\Omega\)(Big-Omega)에 대해서 알아보고자 한다.

\(\Theta\) Notation

\(\Theta\) 표기법이 가지는 의미는 다음과 같다.

\[\eqalign{ &\text{if } \exists \ n_0, c_1, c_2 > 0, \text{ such that } 0 \leq c_1g(n) \leq f(n) \leq c_2 g(n) \text{ where } n_0 \leq n \\ &\text{then } f(n) \in \Theta(g(n)) }\]

즉, \(n_0 \leq n\) 영역에서 조건 \(0 \leq c_1g(n) \leq f(n) \leq c_2 g(n)\)를 만족하는 양의 실수 \(c_1, c_2\)가 존재함을 보이라는 것이다. Introduction to Algorithm에 나와있는 그림을 통해 보면 보다 쉽게 이해할 수 있다.

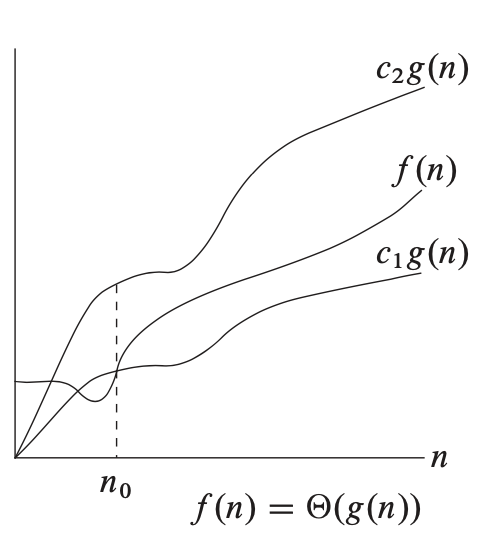
그림에서 볼 수 있듯이 \(c_1g(n)\)은 \(f(n)\)의 하한을, \(c_2g(n)\)은 상한을 표현하고 있다. 이렇게 상한과 하한을 모두 \(g(n)\)의 상수배로 표현하는 것이 \(\Theta\) 표기법의 특징이며, 이러한 점에서 \(\Theta\) 표기법을 점근적으로 엄밀한 한계(Asymptotically tight bound)라고 한다.

\(\Theta\) 표기법 뿐만 아니라 모든 점근적 표기법에서 \(g(n)\)은 어떤 함수로든 주어질 수 있지만, 최고차항 이외의 항들은 모두 무시하고, 최고차항의 계수도 생략하고 표기하는 것이 일반적이다. 예를 들어 \(a,b,c > 0\)일 때 모든 \(an^2 + bn + c\)가 \(\Theta(n^2)\)과 같다는 것은 다음과 같이 보일 수 있다.

\[\eqalign{ &0 \leq c_1 n^2 \leq an^2+bn+c \leq c_2 n^2, \text{where } 0 < n_0 \leq n, 0 < c_1, c_2\\ \Rightarrow&c_1 \leq a + {b \over n} + {c \over n^2} \leq c_2 \\ \Rightarrow& c_1 - c_1 \leq a - c_1 + {b \over n} + {c \over n^2} \leq c_2 - c_1 \\ \Rightarrow& 0 \leq a - c_1 + {b \over n} + {c \over n^2} \leq c_2 - c_1 \leq c_2 \\ }\]

이때 \(n_0 \leq n\)이므로 \(c_2 = a - c_1 + {b \over n_0} + {c \over n_0^2}\)라면 위의 식은 항상 성립한다. 따라서 양의 실수 \(c_1, c_2\)는 항상 존재한다.

\(O\) Notation

\(O\) 표기법은 점근적 상한(Asymptotic Upper Bound)이라고 한다. \(\Theta\) 표기법이 상한과 하한 모두를 제약 조건으로 가진다면 \(O\) 표기법은 상한만을 제약 조건으로 가지기 때문이다.

\[\eqalign{ &\text{if } \exists \ n_0, c > 0, \text{ such that } 0 \leq f(n) \leq c g(n) \text{ where } n_0 \leq n \\ &\text{then } f(n) \in O(g(n)) }\]

보다 직관적으로 풀어쓰자면 \(O(g(n))\)은 모든 \(n \geq n_0\)에 대해 \(0 \leq f(n) \leq c g(n)\)을 만족하는 양의 상수 \(n_0, c\)가 존재하는 함수 \(f(n)\)의 집합이라고 할 수 있다. 그래프로 확인하면 다음과 같다.

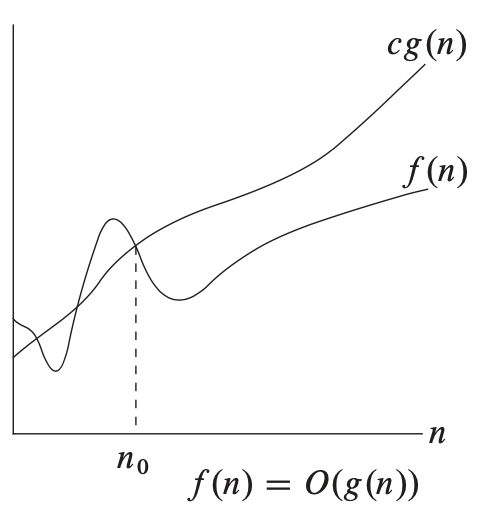
\(O\) 표기법은 수행 횟수의 상한, 즉 최악의 경우를 기준으로 하기 때문에 알고리즘 분석에 가장 많이 사용된다. 한 가지 특징 중 하나는 \(O\) 표기법에서는 하한을 정의하고 있지 않으므로 \(f(n) = n^2\)은 \(f(n) \in O(n^2)\)이면서, \(f(n) \in O(n^3)\), \(f(n) \in O(n^4)\) … 등에도 포함된다는 것이다.

\(\Omega\) Notation

\(\Omega\) 표기법은 점근적 하한(Asymptotic Lower Bound)이라고 한다. 즉 하한만을 제약 조건으로 가진다.

\[\eqalign{ &\text{if } \exists \ n_0, c > 0, \text{ such that } 0 \leq c g(n) \leq f(n) \text{ where } n_0 \leq n \\ &\text{then } f(n) \in O(g(n)) }\]

그래프로 보이면 다음과 같다.